
MMATAN04
.pdf
|
|
|
−9 + 2√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Если t = |
3 |
, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−9 + 2√ |
|
|
|
|
|
|
|
|
|
|
−9 + 2√ |
|
|
|
|
|
|
|||||||||||
|
|
|
|
x2 |
− |
4x = |
3 |
, x2 |
− |
4x |
− |
3 |
= 0, |
|
|||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
± 4 + |
|
|
|
+ 2√ |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
x1,2 = 2 |
−9 |
|
3 |
|
= 2 ± |
|
|
|
9 + 6√3. |
||||||||||||||||||||||||
|
|
|
3 |
|
|
|
|
3 |
|||||||||||||||||||||||||||||
|
|
−9 − 2√ |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
При t = |
3 |
исходное уравнение имеет комплексные корни. |
|||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|||||
2 |
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
2 |
3 |
|
2+ |
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||
|
9+6 |
|
|
|
|
|
|
|
9+6 |
|
3 |
|
|
||||||||||||||||||||||||
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||||||||||||||||||
Рис. 3.23. Знаки производной y
Знаки второй производной указаны на рис. 3.23. График функ-
ции y = |
|
(x − 1)(x − 2)(x − 3) |
выпуклый вниз (y > 0) на интерва- |
||||||||||||||||
2 + |
|
|
|
|
√ |
|
|
|
|||||||||||
ле |
1 |
|
1 |
|
|
1 |
|
|
|
|
|||||||||
|
3 |
|
|
9 + 6 |
|
3, +∞ , выпуклый вверх (y < 0) на интервалах |
|||||||||||||
(1, 2) и 3, 2 + |
|
|
|
|
9 + 6√ |
|
, при x = 2 + |
|
9 + 6√ |
|
имеет точку |
||||||||
|
|
|
|
3 |
3 |
||||||||||||||
3 |
|
3 |
|||||||||||||||||
перегиба. График исследуемой функции изображен |
на рис. 3.24. |
||||||||||||||||||
3. Исследование функции
y = 3 x3 − x2 − x + 1.
I. Область определения — вся действительная ось
X = (−∞, +∞).
Функция общего вида.
151

y
 x
x
Рис. 3.24. График функции y = ±p(x − 1)(x − 2)(x − 3)
Ищем точки пересечения с осями:
x = 0 y = 1, M1(0, 1), y = 0 x3 − x2 − x + 1 = 0,
x3 − x2 − x + 1 |
= x2(x − 1) − (x − 1) = (x |
− 1)(x2 − 1) = (x − 1)2(x + 1), |
(x − 1)2(x + 1) = 0, x = 1, x = −1, |
M2(−1, 0), M3(1, 0). |
|
На рис 3.25 |
показаны интервалы знакопостоянства функции. |
|
y |
|
|
+ |
|
+ |
x |
|
|
|||||
|
|
|
|
|
|
|
1 |
|
1 |
|
|||
|
|
|
||||
Рис. 3.25. Знаки функции y
152

II. Поведение функции на границе области определения: |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
y(+∞) = +∞, |
|
y(−∞) = −∞. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
Вертикальных асимптот нет. Найдем наклонные асимптоты |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
3 |
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
x→±∞ |
|
|
= x→±∞ 1 − |
|
|
|
− |
|
|
+ |
|
|
= 1, |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
x |
x |
x2 |
x3 |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
k = |
lim |
|
|
|
|
|
|
|
|
lim |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
b = lim |
|
|
|
− kx) |
= |
|
lim |
( |
x3 |
− |
x2 |
− |
x + 1 |
− |
x) = |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
x→±∞(y |
3 |
|
|
x→±∞ |
|
|
|
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= |
|
lim |
|
|
|
|
|
|
|
|
|
|
|
( √x3 − x2 − x + 1) |
|
− x |
|
|
|
|
|
|
|
|
|
= |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
→±∞ |
|
(x |
− x − x + 1)x2 |
|
|
|
|
|
|
|
|
|
x2 |
− |
x + 1 + x2 |
|
|
||||||||||||||||||||||||||||||||||
|
x |
|
|
x + 1− |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
3 |
3 |
|
2 |
|
|
|
|
|
|
|
2 + x √x3 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
= |
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
− |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|||
|
x |
→±∞ |
|
(x |
− x − x + 1) |
1 |
|
|
|
|
|
− |
|
x2 |
− |
x + 1 + x2 |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
3 |
3 |
|
2 |
|
|
|
|
|
|
|
2 + x √x3 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 − |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||||||||
= x lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= − |
. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
1 − x |
− x2 |
+ x3 |
+ 3 1 − x |
− x2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
+ x3 + 1 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
→±∞ |
|
|
1 |
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким образом, y = x − |
|
|
— наклонная асимптота. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
3 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
III. Исследование с помощью первой производной |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y = |
1 |
|
|
|
|
3x2 − 2x − 1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 (x3 − x2 − x + 1) 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Найдем критические точки функции: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
3x2 − 2x − 1 = 0, x1 = 1, x2 = − |
|
. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
В точке x = |
|
1 |
производная y |
|
= 0. В точке x = 1 производная |
||||||||||||||||||||||||||||||||||||||||||||||||
|
− |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
не существует, в чем легко убедится, преобразовав выражение для первой производной:
y = |
1 |
(3x + 1)(x − 1) |
= |
1 |
|
3x + 1 |
|
. |
|
|
2 |
|
1 |
|
2 |
||||
3 |
3 |
|
|
||||||
[(x − 1)2(x + 1)] 3 |
|
(x − 1) 3 |
(x + 1) 3 |
|
|||||
153

Откуда видно, что x = −1 — также критическая точка. В точке
1
x = −3 касательная к графику параллельна оси 0x, в точках x = ±1
— параллельна оси 0y.
Знаки первой производной указаны на рис. 3.26.
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
+ |
+ |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.26. Знаки производной y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
Функция возрастает на интервалах −∞, − |
1 |
и |
(1, +∞), убыва- |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
|||||||||||||||||||||||||||||||||||||||||||||||
ет на интервале − |
1 |
, 1 , x = |
1 |
|
— точка максимума, |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
− |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
3 |
3 |
√4. |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
ymax = y |
|
|
−3 |
|
= |
−27 − |
9 + |
3 + 1 = |
|
27 |
= 3 |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
3 |
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
|
3 |
|
|
32 |
2 |
|
3 |
|
|
|
||||||||||||||
|
IV. Исследование с помощью второй производной |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
y = |
|
|
|
|
2 |
|
|
|
(3x2 − 2x − 1)2 |
+ |
1 |
|
|
|
6x − 2 |
|
|
|
|
|
= |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
−9 |
|
|
|
|
|
|
|
|
|
|
5 |
3 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(x3 − x2 − x + 1) 3 |
|
|
|
|
(x3 − x2 − x + 1) 3 |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
= |
− |
2 (3x + 1)2(x − 1)2 − (9x − 3)(x − 1)2(x + 1) = |
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
(x3 − x2 − x |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 1) 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
= |
− |
|
2 (x − 1)2((3x + 1)2 − (9x − 3)(x + 1)) = |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
(x3 − x2 − x |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 1) 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
= |
− |
2 |
|
(x − 1)2(9x2 + 6x + 1 − 9x2 − 6x + 3) |
= |
|
|
8 |
|
|
|
|
|
|
|
|
1 |
|
|
. |
||||||||||||||||||||||||||||
9 |
|
−9 |
|
|
|
|
4 |
|
|
5 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
[(x − |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1)2(x + 1)] 3 |
|
|
|
|
|
|
|
|
|
|
|
|
(x − 1) 3 (x + 1) 3 |
|
||||||||||||||||||||||
154 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

График функции выпуклый вверх (y < 0) на интервале (−∞, −1), |
выпуклый вниз (y > 0) на интервале (−1, +∞), x = −1 — точка |
перегиба. |
График функции изображен на рис. 3.27. |
y |
x |
3 |
Рис. 3.27. График функции y = √x3 − x2 − x + 1 |
Задачи для самостоятельной работы
14.1. y = ± |
x(x2 − 1) |
. |
14.2. y = |
x2(x + 3) |
. |
155

|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
3 |
|
2 |
|
|
|
|
|
||||
14.3. y = 1 + |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
14.4. y = |
3 |
x |
+ x . |
|
|
|
|
|||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Ответы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
14.1. Функция |
общего |
|
вида. |
|
|
О.О.Ф: [−1, 0] [1, +∞). График |
||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
− , |
|
|
|
|
|
∞ |
|
|
|
|
∞; |
= |
|
|
|
|
1 |
|
||||||||||||
симметричен относительно оси |
0x. Для |
y |
' x(x2 |
− 1) имеем: |
||||||||||||||||||||||||||||||||||||
y(0) = y(1) = |
|
y( 1) |
y(+ |
|
|
|
|
|
) |
= + |
возрастает |
на интерва- |
||||||||||||||||||||||||||||
лах |
−1, −√ |
|
|
|
|
и (1, +∞), |
убывает на |
интервале |
−√ |
|
, 0 ; |
|||||||||||||||||||||||||||||
3 |
|
3 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ymax |
= |
|
y −√ |
|
|
= |
3√ |
|
|
; график выпуклый вверх на интер- |
||||||||||||||||||||||||||||||
3 |
3 |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
валах (−1, 0) и |
|
1, 1 + |
|
√3 , выпуклый |
|
вниз на интервале |
||||||||||||||||||||||||||||||||||
|
3 |
|
||||||||||||||||||||||||||||||||||||||
1 + 3 |
√3, +∞ , x = 1 + 3 |
√3 — точка перегиба. |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
14.2. Функция общего вида. О.О.Ф: [−3, +∞); y(−3) = y(0) = 0, y(+∞) = +∞; возрастает на интервалах (−3, −2) и (0, +∞), убывает на интервале (−2, 0), ymax = y(−2) = 2; график функции выпуклый вверх на интервале (−3, 0) и выпуклый вниз на интервале (0, +∞).
14.3.Функция общего вида. О.О.Ф: (−∞, −1] '(0, +∞);
y(−∞) = 1 − 0, y(−1) = 0, y(+0) = +∞, y(+∞) = 1 + 0; x = 0 — вертикальная асимптота, y = 1 — горизонтальная асимптота; убывает на интервалах (−∞, −1) и (0, +∞); график выпуклый
вверх на интервале (−∞, −1) и выпуклый вниз на интервале
(0, +∞).
14.4. Функция общего вида. О.О.Ф: (−∞, +∞); y(−1) = y(0) = 0; y ≥ 0 при x ≥ −1, y < 0 при x < −1; y(−∞) = −∞, y(+∞) = +∞;
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = |
x + |
|
|
|
|
|
— |
наклонная асимптота; |
возрастает на |
интерва- |
|||||||
3 |
2 |
|
|||||||||||||||
|
−∞, − |
|
|
|
|
|
|
|
|
|
2 |
, 0 ; |
|||||
лах |
|
|
|
и |
(0, +∞), убывает |
на |
интервале |
− |
|
||||||||
3 |
3 |
||||||||||||||||
|
|
|
|
2 |
|
|
1 |
3 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ymax |
= y − |
|
|
|
= |
|
√4, ymin = y(0) |
= |
0, M (0, 0) — угловая |
||||||||
3 |
3 |
||||||||||||||||
точка; график выпуклый вверх на интервалах (−1, 0) и (0, +∞), выпуклый вниз на интервале (−∞, −1).
156

Занятие 15. Исследование тригонометрические функций
Задание
Исследовать функцию и построить график.
1. y =
3. y =
sin x
2 + cos x .
x
2 + arcctg x.
2. |
y = sin x + cos2 x. |
||
4. |
y = arcsin |
2x |
|
|
. |
||
1 + x2 |
|||
Решения
sin x
1. Исследование функции y = 2 + cos x .
I. Область определения — вся действительная ось
X = (−∞, +∞).
Функция периодическая с периодом T = 2π. Функция нечетная; основная область исследования −π ≤ x ≤ π.
Точки пересечения с осями: M1(−π, 0), M2(0, 0), M3(π, 0).
Интервалы знакопостоянства (совпадают со знаком функции sin x): y > 0 на интервале (0, π); y < 0 на интервале (−π, 0).
II. Поведение функции на границе основной области исследования:
y(−π) = 0, y(π) = 0,
Асимптот нет.
III. Исследование с помощью первой производной
y = |
cos x(2 + cos x) + sin2 x |
= |
2 cos x + 1 |
|
|
|
. |
||
(2 + cos x)2 |
(2 + cos x)2 |
|||
157

Производная равна нулю (y = 0), если |
|
|
|
|
|
|
||
2 cos x + 1 = 0, cos x = − |
1 |
, |
|
|||||
|
|
|||||||
2 |
|
|||||||
1 |
|
|
2π |
|
||||
x = ± arccos − |
|
+ 2kπ, |
x ± |
|
|
|
|
+ 2kπ. |
2 |
|
3 |
|
|
||||
2π
В области −π ≤ x ≤ π получаем два решения при k = 0: x1 = − 3
2π
и x = 3 . Определим знаки производной (при решении тригонометрических неравенств используем рис. 3. 28):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
+ |
|
1 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.28. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
y > 0, |
2 cos x + 1 |
> 0, |
|
|
|
cos x > − |
1 |
, |
|
|
− |
2π |
< x < |
2π |
, |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
2 |
|
|
3 |
3 |
||||||||||||||||||||||||||||||
y < 0, |
cos x < − |
1 |
|
|
|
|
|
−π < x < − |
2π |
|
|
|
2π |
|
|
|
|||||||||||||||||||||
|
|
, |
|
|
|
|
|
, |
|
|
|
|
|
< x < π. |
|
||||||||||||||||||||||
2 |
|
|
|
3 |
|
|
3 |
|
|
||||||||||||||||||||||||||||
Функция возрастает на интервале − |
|
2π |
, |
2π |
|
и убывает на ин- |
|||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
3 |
3 |
|
|||||||||||||||||||||||||||||||||||
тервалах −π, − |
2π |
2π |
, π ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
158 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
√3 |
√3 |
|
|
|
|
√3 |
√3 |
||
ymax = y |
2π |
|
2 |
|
ymin = y − |
2π |
− 2 |
|||||
3 = |
2 |
− |
1 = |
3 , |
3 = |
2 |
− |
1 |
= − 3 . |
|||
|
|
|
2 |
|
|
|
|
|
2 |
|
||
IV. Исследование с помощью второй производной |
|
|
|
|
||||||||
y = −2 sin x(2 + cos x)2 − (2 cos x + 1)2(2 + cos x)(− sin x) = |
||||||||||||
|
|
|
|
|
(2 + cos x)4 |
|
|
|
|
|
||
|
= −2 sin x(2 + cos x) + 2 sin x(2 cos x + 1) |
= |
|
|
||||||||
|
|
|
|
|
(2 + cos x)3 |
|
|
|
|
|
||
|
|
2 sin x(cos x − 1) = |
4 sin x sin2 x |
|
|
|
|
|||||
|
= |
|
2 . |
|
|
|
|
|||||
|
|
|
(2 + cos x)3 |
|
− (2 + cos x)3 |
|
|
|
|
|||
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
−π |
|
|
π |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
sin x |
|
|
|
|
|
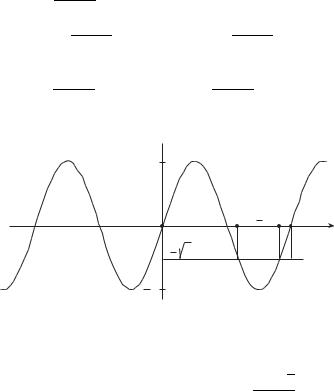
Рис. 3.29. График функции y = 2 + cos x |
|
|
|
|
|||||||
График функции выпуклый вверх (y < 0 sin x > 0) на интервале (0, π), выпуклый вниз (y > 0 sin x < 0) на интервале (−π, 0),
x = 0 — точка перегиба. График функции изображен на рис. 3.29.
159
2.Исследование функции y = sin x + cos2 x.
I. Область определения — вся действительная ось
|
|
|
|
|
|
|
|
|
X = (−∞, +∞). |
|
|
|
|
|
|||||||
|
Функция периодическая с периодом T = 2π; основная область |
||||||||||||||||||||
исследования 0 ≤ x ≤ 2π. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Найдем нули функции (точки пересечения с осью 0x): |
||||||||||||||||||||
|
sin x + cos2 x = 0, |
sin x + 1 − sin2 x = 0, |
|
|
sin2 x − sin x − 1 = 0, |
||||||||||||||||
|
|
1 ± √ |
|
|
; |
|
sin x = |
1 + √ |
|
> 1 — решений нет, |
|||||||||||
|
sin x = |
5 |
5 |
||||||||||||||||||
|
2 |
|
|
|
|
||||||||||||||||
|
|
|
√ |
|
|
|
|
2 |
|
|
|
|
|
|
1 − √ |
|
|
||||
|
sin x = |
1 − |
|
|
|
|
|
|
|
|
|
+ nπ. |
|||||||||
|
5 |
, |
x = ( |
1)n arcsin |
5 |
||||||||||||||||
|
|
|
|
|
2 |
|
|||||||||||||||
|
|
2 |
|
|
|
|
− |
|
|
|
|
|
|
|
|||||||
Выделим нули на сегменте [0, 2π]: |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
√ |
|
− 1 |
|
|
|
|
arcsin |
√ |
|
− 1 |
|
||||||||
x |
= π + arcsin |
5 |
x |
= 2π |
− |
5 |
|||||||||||||||
|
|
|
|
||||||||||||||||||
1 |
|
2 |
|
, |
|
2 |
|
|
|
|
|
|
2 |
|
|
||||||
M (0, 1) — точка пересечения с осью 0y. |
|
|
|
|
|
||||||||||||||||
y 
1
y = sin x
+ + +
0 |
π x1 x2 2π x |
1 5
2
1
Рис. 3.30.
Определим интервалы знакопостоянства функции:
√
y > 0, sin x + cos2 x > 0, sin2 x − sin x − 1 < 0, 1 − 5 < sin x ≤ 1. 2
Решение последнего неравенства показано на рис. 3.30.
160
