
MMATHAN05
.pdf
B |
r=r(ϕ) |
|
|
|
|
|
|
S |
|
1 |
β |
|
|
|
|
α |
|
|
||
|
αA |
S = |
|
r2(ϕ) dϕ. |
(4.6) |
|
β |
2 |
O
Рис. 4.4
Задание
Найти площади фигур, ограниченных кривыми.
1.y = 2x − x2, x + y = 0.
2.y = (x + 1)2, x = sin πy, y = 0 (0 ≤ y ≤ 1).
3.x = a(t − sin t), y = a(1 − cos t) (0 ≤ t ≤ 2π).
4.x = 2t − t2, y = 2t2 − t3 (0 ≤ t ≤ 2).
5.x2 + y2 = 1. a2 b2
6.r = a sin 3ϕ.
7.(x2 + y2)2 = 2a2(x2 − y2).
Решения
1. Требуется найти площадь фигуры, заключенной между параболой y = 2x − x2 и прямой x + y = 0 (рис. 4.5).
Полагаем в формуле (4.1) y2(x) = 2x − x2, y1(x) = −x. Для нахождения промежутка интегрирования решаем систему уравнений
x + y =−0, |
y1 |
= 0, |
y2 |
= 3. |
y = 2x x2, |
x1 |
= 0, |
x2 |
= 3, |
−
161




 π
π
Рис. 4.5 Рис. 4.6
Тогда
3 |
|
|
|
3 |
|
|
|
3 |
|
S = 0 |
(y2(x) − y1(x)) dx = 0 |
(2 − x2 − (−x)) dx = 0 |
(3x − x2) dx = |
||||||
|
= |
|
2 |
− 3 |
3 |
= 2 − 9 = |
2 . |
|
|
|
|
|
|
||||||
|
|
|
3x2 |
x3 |
0 |
27 |
9 |
|
|
2. При вычислении площади фигуры ABCDA (рис. 4.6), ограниченной кривыми y = (x + 1)2, x = sin πy, y = 0 (0 ≤ y ≤ 1), воспользуемся формулой (4.2), полагая в ней x2(y) = sin πy, x1(y) = −1+√y.
Тогда
|
1 |
|
|
|
1 |
(sin πy − (−1 + √ |
|
|
|
|
|
|
S = 0 |
(x2(y) − x1(y)) dy = |
0 |
|
)) dy = |
||||||||
y |
||||||||||||
1 |
sin πy + 1 − y |
2 |
dy = −π cos πy + y − |
3 y |
2 |
1 |
= |
|||||
= |
0 |
|||||||||||
0 |
|
|
1 |
|
|
1 |
2 |
|
3 |
|
|
|
=π1 + 1 − 23 + π1 = π2 + 13 .
3.Нужно найти площадь фигуры, ограниченной первой аркой
162

циклоиды x = a(t −sin t), y = a(1 −cos t) (0 ≤ t ≤ 2π) и осью абсцисс (рис. 4.7).
 π
π
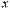
Рис. 4.7 |
Рис. 4.8 |
2πa
По формуле (4.1) S = y(x) dx. После замены x = a(t − sin t),
0
0 ≤ t ≤ 2π, получаем y = y(x(t)) = a(1 − cos t) и
2π |
|
|
|
2π |
1 |
|
|
|
|
1 + |
cos 2t |
dt = |
|||
S = 0 |
a2(1 − cos t)2 dt = a2 |
0 |
− 2 cos t + |
||||||||||||
|
|
||||||||||||||
|
2 |
|
|||||||||||||
|
= a2 |
|
2 t − 2 sin t + |
|
4 |
|
2π |
= 3πa2. |
|
||||||
|
|
|
|
|
|||||||||||
|
|
|
3 |
|
|
sin 2t |
0 |
|
|
|
|
|
|||
4. Площадь фигуры (рис. 4.8), ограниченной петлей параметрически заданной кривой x = 2t−t2, y = 2t2 −t3 (0 ≤ t ≤ 2), вычисляем
по формуле (4.4). Имеем
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 t3 |
− 2 t4 + |
5 t5 |
2 |
= |
|
|
|
|||||||
|
|
|
S = (2t − t2)(4t − 3t2) dt = |
0 |
|
|
|
||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
8 |
|
5 |
|
|
3 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= t3 |
|
3 |
− 2 t + |
5 t2 |
|
2 |
= 8 3 − 5 + |
5 |
|
|
|
|
|
|
|
|
|
= 15 . |
|||||||||
|
|
|
= 8 · 40 − 15 |
|
|||||||||||||||||||||||
|
|
|
8 |
5 |
|
3 |
|
0 |
|
8 |
|
12 |
|
|
|
|
|
75 + 36 |
8 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. Найдем площадь |
фигуры (рис. 4.9), ограниченной эллипсом |
|||||||||||||||||||||||||
x2 |
+ |
y2 |
|
= 1. Используя параметрическое представление эллипса |
|||||||||||||||||||||||
a2 |
|
||||||||||||||||||||||||||
|
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
163 |
||
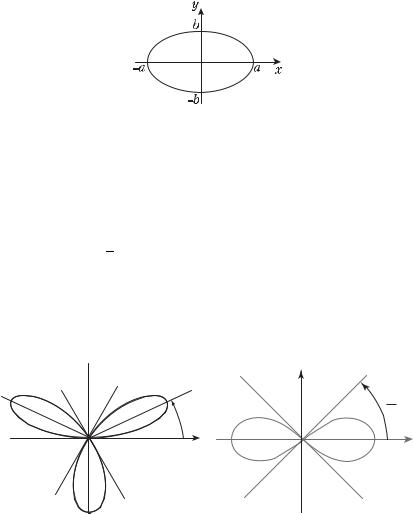
Рис. 4.9
x = a cos t, y = b sin t, 0 ≤ t ≤ 2π, площадь фигуры, ограниченной эллипсом, удобно искать по формуле (4.3)
2π
S = 12 (a cos t b cos t − b sin t(−a sin t)) dt =
|
|
0 |
|
|
|
|
= 2 |
2π |
2 |
2π |
dt = πab. |
||
0 |
(cos2 t + sin2 t) dt = |
0 |
||||
|
ab |
|
|
ab |
|
|
|
y |
|
π |
π |
|
4 |
||
6 |
||
|
x
Рис. 4.10 |
Рис. 4.11 |
6. Найдем площадь фигуры (рис. 4.10), ограниченной кривой, заданной в полярных координатах уравнением r = a sin 3ϕ (a > 0).
164

По формуле (4.6) имеем
|
|
π |
|
|
|
π |
|
|
|
|
π |
|
|
1 |
6 |
|
|
|
6 |
|
|
|
3a2 |
6 |
|
||
0 |
(a sin 3ϕ)2 dϕ = 3a2 |
0 |
sin2 3ϕ dϕ = |
0 |
(1 − cos 6ϕ) dϕ = |
||||||||
S = 6 |
|
|
|||||||||||
2 |
2 |
||||||||||||
|
|
|
= 2 ϕ − |
6 |
π |
= |
4 . |
|
|||||
|
|
|
|
|
|||||||||
|
|
|
|
3a2 |
|
|
sin 6ϕ |
6 |
|
πa2 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7. Требуется найти площадь фигуры |
(рис. 4.11), ограниченной |
||||||||||||
лемнискатой (x2 + y2)2 = 2a2(x2 − y2). |
|
|
|
|
|||||||||
Перейдем к полярным координатам, полагая x = r cos ϕ, y = r sin ϕ. Тогда
r4 = 2a2(cos2 ϕ − sin2 ϕ), r2 = 2a2 cos 2ϕ,
и уравнение лемнискаты принимает вид r = a√2 cos 2ϕ , а искомая площадь равна
|
π |
|
|
|
π |
|
|
|
4 |
|
|
|
|
||
S = 4 2 |
2a2 cos 2ϕ dϕ = 4a2 |
2 |
0 |
= 2a2. |
|||
|
|||||||
1 |
0 |
|
sin 2ϕ |
|
4 |
|
|
Задачи для самостоятельной работы
Найти площади фигур на плоскости, ограниченных кривыми.
1.ax = y2, ay = x2.
2.y = x2, x + y = 2.
3. y = | lg x|, y = 0, x = 0,1, x = 10.
4.y = 2x, y = 2, x − 0.
5.y = x, y = x + sin2 x (0 ≤ x ≤ π).
a3
6. y = x2 + a2 , y = 0.
165

7.y2 = x2(a2 − x2).
8.x = a(2 cos t − cos 2t), y = a(2 sin t − sin 2t).
9.r = a(1 + cos ϕ) (кардиоида).
10.(x2 + y2)2 = 2a2xy (лемниската).
Ответы
|
|
a3 |
|
9 |
|
|
9, 9 |
8, 1 |
|
2 |
1 |
|
π |
|
4 |
|
6πa2. |
||||
1. |
|
|
. 2. |
|
|
. |
3. |
− |
|
. 4. |
− |
|
. 5. |
|
. 6. πa2. 7. |
|
a3. 8. |
||||
3 |
2 |
ln 10 |
ln 2 |
2 |
3 |
||||||||||||||||
9. |
3πa2 |
. |
10. a2. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Занятие 2. Вычисление длин плоских кривых
Длина L кривой, соединяющей точки A и B, может быть вычислена по очевидной формуле
|
L |
|
|
|
L = 0 |
ds, |
(4.7) |
|
|||
Рис. 4.12 |
где s — длина дуги кривой, отсчитыва- |
||
емая от точки A или от точки B. |
|
||
Если гладкая кривая задана параметрически
y = y(t) |
, t0 ≤ t ≤ T, |
x = x(t) |
|
то длина дуги s представляет функцию s = s(t), s(t0) = 0, s(T ) = L, а дифференциал дуги ds равен
(
ds = x 2 (t) + y 2 (t) dt.
166

Производя в формуле (4.7) замену переменной s = s(t), получаем, что длина гладкой кривой, заданной параметрически равна
T |
|
L = (x 2 (t) + y 2 (t) dt. |
(4.8) |
t0
Если кривая задана в явном виде y = y(x), a ≤ x ≤ b, то взяв в качестве параметра t = x получаем в этом случае, что
(
ds = 1 + y 2 (x) dx, и формула (4.8) принимает вид
b |
|
L = (1 + y 2 (x) dx. |
(4.9) |
a
Если кривая задана уравнением x = x(y), c ≤ y ≤ d, то полагая в
(
(4.8) t = y, получаем ds = x 2 + 1 dy, и
d |
|
L = (x 2 + 1 dy. |
(4.10) |
c
Наконец, случай полярного задания кривой r = r(ϕ), α ≤ ϕ ≤ β, также приходим к параметрическому заданию
x = r(ϕ) cos ϕ, y = r(ϕ) sin ϕ, α ≤ ϕ ≤ β.
В этом случае
(
ds = x 2 (ϕ) + y 2 (ϕ) dϕ =
= (r cos ϕ − r sin ϕ)2 + (r sin ϕ + r cos ϕ)2 dϕ =
(
=r2 (cos2 ϕ + sin2 ϕ) + r 2 (cos2 ϕ + sin2 ϕ) dϕ =
(
=r2 (ϕ) + r 2 (ϕ) dϕ
и
β |
|
|
|
|
L = α |
( |
r2 (ϕ) + r 2 (ϕ) |
dϕ. |
(4.11) |
|
|
|
|
167 |

Задание
Найти длины дуг следующих кривых:
1.y = a ch xa от точки A(0, a) до точки B(b, h).
2.y = ex, (0 ≤ x ≤ x0).
3. |
x = a ln a + |
y |
− |
|
− a2 |
− y2 |
(0 < b ≤ y ≤ a). |
|||
|
|
|
|
|
a2 |
|
y2 |
|
|
|
|
2 |
2 |
|
2 |
|
|
|
|
|
|
4. |
x 3 |
+ y 3 = a 3 (астроида). |
|
|
||||||
5. |
x = cos4 t, |
y = sin4 t. |
|
|
||||||
6.r = a(1 + cos ϕ) (кардиоида).
7.r = a emϕ (m > 0) при 0 < r < a.
Решения
1. Найти длину дуги кривой y = a ch |
x |
от точки A(0, a) до точки |
|||||||
a |
|||||||||
B(b, h) (рис. 4.13). |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
y |
B |
y |
|
|
|
|||
|
|
|
|
||||||
|
h |
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
|
A |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
b |
|
x |
1 |
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
0 |
|
x |
x |
|
|
|
|
|
|
|
|
0 |
|
|
|
Рис. 4.13 |
|
|
|
|
|
Рис. 4.14 |
|
|
|
|
|
|
|
|
|
|||
168 |
|
|
|
|
|
|
|
|
|

По формуле (4.9) имеем
b |
|
|
|
|
|
b |
|
|
|
|
a |
|
|
|
L = |
|
1 + sh 2 a |
dx = |
|
ch a dx = a sh a |
0 |
= a sh a = |
|||||||
0 |
|
|
x |
0 |
|
x |
|
x |
|
|
b |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
h2 |
|
|
|
|||
= a ch 2 |
− 1 = a |
h2 − a2. |
|||||||
|
|
|
− 1 = |
||||||
a |
a2 |
||||||||
2. Найти длину дуги кривой y = ex, (0 ≤ x ≤ x0) (рис. 4.14).
По формуле (4.9) имеем
x0
|
|
L = |
|
|
|
dx. |
|
|
|
|
|||||
|
|
0 |
|
1 + e2x |
|
|
|
|
|||||||
Сделаем замену |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
1 |
|
|
|
|
t dt |
|
|||
1 + e2x = t, x = |
ln(t2 − 1), |
dx = |
, |
||||||||||||
|
|
|
|
||||||||||||
|
2 |
t2 − 1 |
|||||||||||||
|
x = 0 t = √ |
2 |
, x = x0 |
1 + e2x0 |
. |
|
|||||||||
Тогда
√√
|
1+ e2x0 |
t2 |
|
|
|
|
|
|
1+ e2x0 |
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|||||||||||||
L = |
|
|
|
|
dt = |
1 + |
|
|
|
|
|
− |
|
dt = |
||||||||||||||||||||||
|
|
t2 − 1 |
|
|
|
2 |
|
t − 1 |
|
t + 1 |
||||||||||||||||||||||||||
|
√ |
2 |
|
|
|
|
|
|
|
|
|
|
√ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
t + 1 |
1+ e2x0 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
= |
|
t + |
1 |
ln |
t − 1 |
√2 |
|
|
= |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
√1 + e |
2x0 |
|
|
|
|
|
|
|
1 |
|
√2 |
|
|
1 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
2x0 |
|
|
|
|
1 |
|
|
|
|
|
√2 |
|
|
|
|
|||||||||||||||
= |
1 + |
e |
|
+ |
|
|
|
ln |
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
ln |
|
|
− |
|
= |
||||||
|
|
|
|
|
|
2 |
|
|
√1 + e2x0 |
+ 1 |
− |
|
|
− 2 |
|
√2 + 1 |
|
|||||||||||||||||||
169

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
1 |
|
|
|
(√ |
|
|
|
|
|
|
|
|
|
|
|
− 1)(√ |
|
+ 1) |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
ln |
1 + e2x0 |
2 |
= |
||||||||||||||||||||||||||||||||||||||||||||||||
= |
|
|
1 + |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
e |
2x0 |
|
|
|
|
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
(√1 + e2x0 + 1)(√2 − 1) |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
1 |
|
|
|
|
(√ |
|
|
|
|
|
|
|
|
|
− 1)2(√ |
|
+ 1)2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
ln |
1 + e2x0 |
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
1 + |
|
|
|
|
|
|
|
|
|
|
= |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
e |
2x0 |
− |
2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e2x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
= |
1 + e2x0 |
− √ |
|
− x0 + ln( |
1 + e2x0 |
|
|
− 1)(√ |
|
|
+ 1). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3. Найти длину дуги кривой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
x = a ln |
a + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− a2 − y2 |
(0 < b ≤ y ≤ a). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
y |
|
− |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Вычислим производную от функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
x(y) = a(ln(a + |
|
|
|
|
|
|
|
|
) − ln y) − |
|
|
|
|
|
. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
a2 − y2 |
a2 − y2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Имеем |
|
|
|
|
|
|
|
|
a + |
|
a2 |
|
− y2 · |
a2 |
− y2 |
− y |
|
|
|
|
a2 − y2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x (y) = a |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−y |
|
|
|
|
|
1 |
|
|
|
|
+ |
|
|
|
|
|
y |
|
|
|
|
= |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 1 − a + a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
= −y + |
|
|
|
a2 |
|
|
|
|
|
|
|
y2 = |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
− |
|
|
|
|
|
|
|
a |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
− y |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
= |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
a − y |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
y2 |
2 |
|
2 |
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
−y |
|
|
a2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
a + |
|
|
|
|
a2 |
|
|
|
y2 − y |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
y(a + a |
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
y ) |
|
|
|
|
|
|
|
|
|
|
|
y(a + |
a |
|
|
|
|
y |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
= |
y − a |
2 |
− a a − y |
|
|
|
|
= |
|
|
|
|
|
|
|
a − y ( a − y + a) |
= |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
− |
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
− |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= − |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a y− y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Длину дуги кривой вычисляем, используя формулу (4.10). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
L = |
|
|
a2 |
− y2 |
+ 1 dy = |
|
|
|
|
a |
dy |
= a ln y |
|
|
|
= a ln |
a |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4.Найти длину астроиды x 3 |
+ y 3 |
|
|
= a 3 |
(рис. 4.15). |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
170 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
