Определение синуса, косинуса и тангенса, котангенса угла

Теорема Пифагора

sin²a+cos²a=1

знаки синуса и косинуса

равенство углов равнобедренного треугольника

синус, косинус, тангенс углов a и –a

sin(-a)=sina

cos(-a)=cosa

формула расстояния между двумя точками

формулы сложения

формулы приведения

сумма и разность синусов, сумма и разность косинусов

синус и косинус двойного угла

синус и косинус половинного угла

понижение степени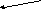

Рис. 7 Структурно-логическая схема тригонометрической функции

На рисунке 7 изображена СЛС тригонометрической функции представляющая структуру освоенного содержания обучения. Первичными УЭ являются «Определение синуса, косинуса и тангенса угла» и «Формулы сложения» (на рисунке они выделены полужирным шрифтом), т.к. из них путем несложных преобразований получаются все остальные УЭ тригонометрической функции. Именно поэтому мы считаем необходимым включить в объем запоминаемого содержания обучения эти элементы.

Анализируя СЛС, демонстрирующие взаимосвязь степенной, показательной и логарифмической функций (см. рис.8) можно отметить, что определения функций являются исходными УЭ и на наш взгляд должны быть обязательно включены в объем запоминаемого содержания обучения. Свойства показательной и логарифмической функций являются следствиями свойств степенной функции, поэтому к первичным УЭ можно отнести именно свойства степенной функции.

Рис. 8 СЛС, демонстрирующие взаимосвязь УЭ степенной, показательной и логарифмической функций

На основе структурно-логических схем были построены таблицы, где выделены операции (или логические шаги), которые необходимо выполнить для получения формулы. Просчитав количество этих операций, можно судить о сложности получения УЭ. На основании проведенного анализа таблиц по тригонометрической функции можно отметить, что необходимо выполнить наибольшее число операций (а именно 9) для получения формулы сложения аргументов косинусов, а наименьшее число операций (2) для получения формулы зависимости тангенса и котангенса и формул двойного аргумента.

Затем был проведен сравнительный анализ утвержденного обязательного минимума основных образовательных программ полного общего образования и содержания признанных тестов достижений (ЕГЭ и ЦТ).

На основании полученных результатов можно отметить следующее:

• все элементы минимума содержания отображены в школьной программе и исключений нет;

• в указанной совокупности тестов достаточно часто используются учебные элементы формально не входящие в обязательный минимум содержания, например, теорема Пифагора;

• не все элементы минимума содержания используются в отдельных батареях тестов;

• часть элементов содержания не используется в исследованных батареях представленных выше тестовых систем;

• в задачах есть примеры выхода за пределы обязательного минимума содержания;

• количество применяемых учебных элементов больше числа заданий;

• имеет место не эквивалентность вариантов по содержанию, что противоречит условию стандартизации тестов.

Выделенные в результате анализа структурно-логических схем учебные элементы содержания были максимально однозначно описаны и проанализированы на частотность использования в тестах достижений ЕГЭ и ЦТ [32, 33, 41]. Смысл частотного анализа – определить долю (процент) использования УЭ в анализируемых заданиях тестов.

Поскольку правильно выполненные операции, действия с этими УЭ определяют успешность выполнения теста в целом, частотность использования этих УЭ, независимо от степени осознанности их включения в задания тестов, пропорциональна значимости усвоения данных УЭ.

Представим теперь описание объекта, процедуры и результатов частотного анализа тестов ЦТ и ЕГЭ.

Конкретно, проведен частотный анализ следующих тестовых заданий: ЕГЭ 2001г. - 10 вариантов по 25 заданий в каждом [57]; ЕГЭ 2002г. – демонстрационный вариант - 25 заданий [58]; ЕГЭ 2003г. – демонстрационный вариант - 30 заданий [59]; ЦТ 1999г. – пять вариантов по 20 заданий [98]; ЦТ 2000г. – десять вариантов по 20 заданий [99]; ЦТ 2002г. – 9 вариантов по 22 задания [100].

Решая проблему однозначности выделения, описания рассматриваемых УЭ, мы, отказавшись от предлагаемой в процедуре ЕГЭ их классификации, выделили перечень УЭ на основе СЛС представления функций в комплектах учебников школьной математики и разработанных СЛС, представляющих структуру освоенного знания (см. табл. Приложения 2). При этом ввели следующее описание УЭ:

• Степенная функция – любая, используемая в тестовых заданиях и в их решении, функция вида: х^s , s – действительное число, не равное нулю или единице, а х > 0².

• Показательная функция – любая, используемая в тестовых заданиях и в их решении, функция вида: а^х , где а и х действительные величины, а ≥ 0.

• Логарифмическая функция – любая, используемая в тестовых заданиях и в их решении, функция вида: log_аx, где а и х действительные, положительные величины.

• Тригонометрические функции соответствуют своему традиционному для школьной математики геометрическому определению, в котором х – действительное число, cosx, sinx, tgx, ctgx – соответствующие тригонометрические функции.

• свойства функций, для однозначности представляемые их аналитическим выражением.

Для определения частотности использования в тестах самих функций и их конкретных свойств прорешены все задачи в представленных выше вариантах и составлена таблица (См. приведенную в качестве примера обобщенную таблицу 1).

Таблица 1.

Частотность использования элементарных функций в тестах Централизованного тестирования и Единого государственного экзамена

Сред. в %	ЦТ 99	ЦТ 00	ЦТ 02	ЕГЭ 01	ЕГЭ 02	ЕГЭ 03	Сред. в %	Ст. Откл (S)
Степенная функция	71,82	86	78,50	69,60	68,00	70,00	74,29	8,47
Показательная функция	5,45	8,35	9,59	12,80	16,00	17,00	11,62	4,38
Логарифмическая функция	9,09	13,63	9,09	16,40	12,00	20,00	13,52	4,11
Тригонометрическая функция	15,45	20,55	18,18	30,40	24,00	20,00	21,69	4,89
Всего:	101,81	130,55	115,36	140,20	120,00	127,00	121,12	7,01

Первая строка в списке УЭ таблицы 1 - «Наличие степенной функции» объединяет все описанные выше представления степенной функции и, традиционно выделяемые в школьной математике корни степени n. Конкретные задания могут содержать УЭ не только одной функции, поэтому их суммарный процент превышает 100%.

В таблицах частотности по вариантам (см. таблицу 2): в строках содержатся описания УЭ школьной программы, а в столбцах – частотность использования данного УЭ в анализируемом варианте теста. При этом:

• Любая переменная, любое число в первой степени не учитывается как степенная функция.

• Любой УЭ одного задания учитывается только один раз.

Таблица 2.