Операции с векторами:
> # Скалярное произведение векторов;
> dotprod(v[1],v[2]);
> dotprod(s[1],s[2]);
> dotprod(alpha[1],alpha[2]);
> # Векторное произведение векторов;
> crossprod(v[1],v[2]);
> crossprod(s[1],s[2]);
> crossprod(alpha[1],alpha[2]);
> # Смешанное произведение векторов;
> dotprod(crossprod(alpha[1],alpha[2]),alpha[3]);
> # Угол между векторами;
> angle(alpha[1],alpha[2]);
> evalf(%);
> norm(alpha[1],3); evalf(%);# Норма трехмерного вектора;
> normalize(alpha[1]);# Нормировать вектор;
> Basis([u[1],u[2],u[3]]);# Нахождение базиса векторов, задаваемых только как u[i] (пакет LinearAlgebra);
> GramSchmidt([u[1],u[2],u[3]]); # Ортогонализация системы векторов векторов, задаваемых только как u[i] (пакет LinearAlgebra);
> convert(alpha[1],list[1]);# Преобразование вектора в список;
Способы задания матриц:
> restart: with(linalg):
Warning, the protected names norm and trace have been redefined and unprotected
> C:=matrix(3,3);
> C1:=array(1..3,1..3);
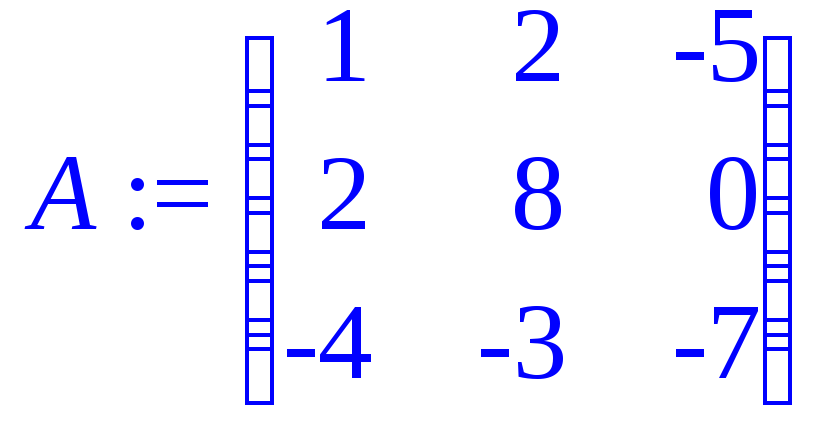
> A:=matrix(3,3,[1,2,-5,2,8,0,-4,-3,-7]);
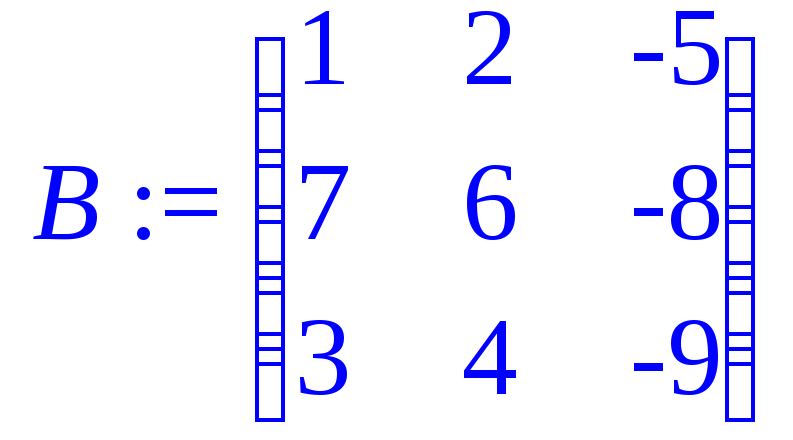
> B:=matrix(3,3,[1,2,-5,7,6,-8,3,4,-9]);
> C2:=matrix(2,3,[1,2,3,4]);
> C3:=array(1..3,1..3,[[1,2,-5],[2,8,0],[-4,-3,-7]]);
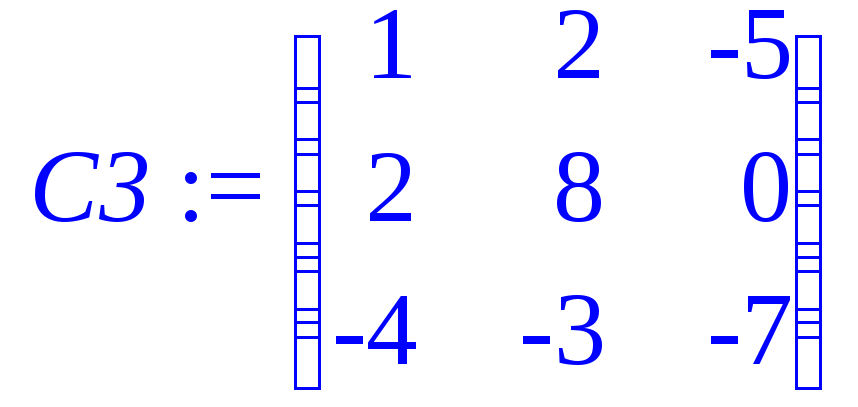
> C4:=array(1..3,1..3,[[1,2,-5],[7,6,-8],[3,4,-9]]);
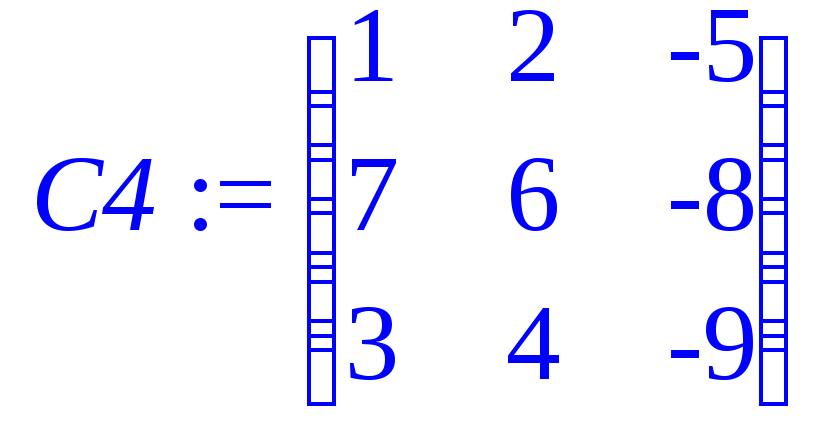
Операции над матрицами:
> rowdim(A); # Число строк матрицы;
> coldim(A); # Число столбцов матрицы;
> evalm(C3+C4);# Сложение (вычитание) матриц;
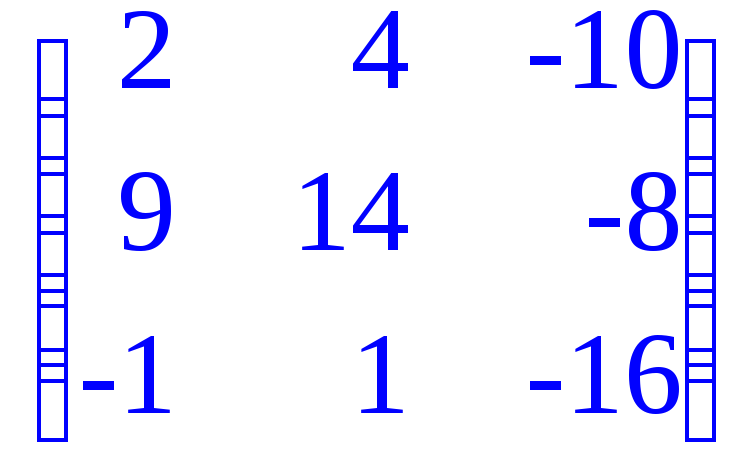
> matadd(C3,C4);# Сложение матриц;
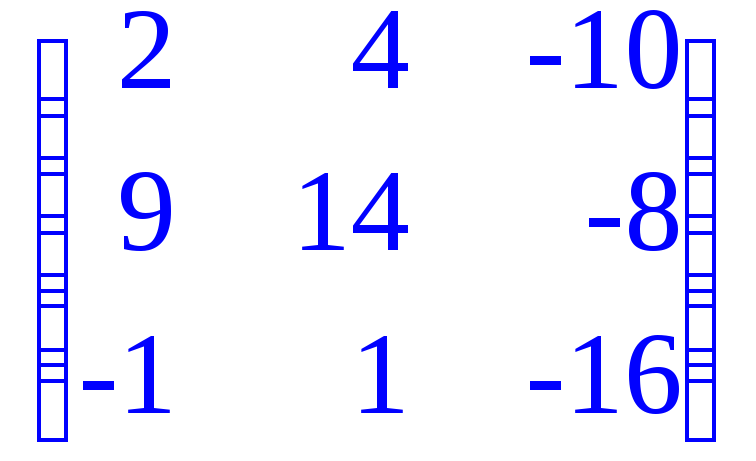
> multiply(C3,C4);#Перемножение матриц;
> evalm(C3&*C4);#Перемножение матриц;
> evalm(2*C3); # Умножение матрицы на число;
> evalm(2+C4);# Сложение матрицы с числом, умноженным на единичную матрицу;
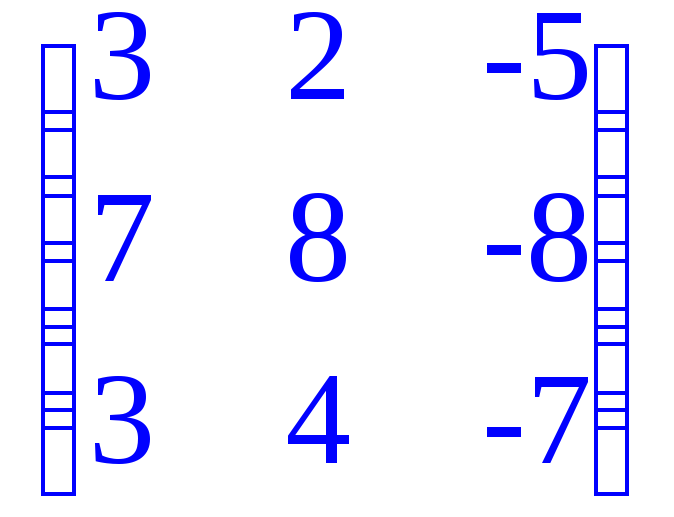
> evalm(C3^3);# Возведение матрицы в степень;
> evalm(A^(-1));# Нахождение обратной матрицы;
> inverse(A); # Нахождение обратной матрицы;
> C:=A^3+4*A+5;# Матрица - функция от матрицы;
> evalm(C);
> evalm(A^0);
> transpose(A);# Нахождение транспонированной матрицы;
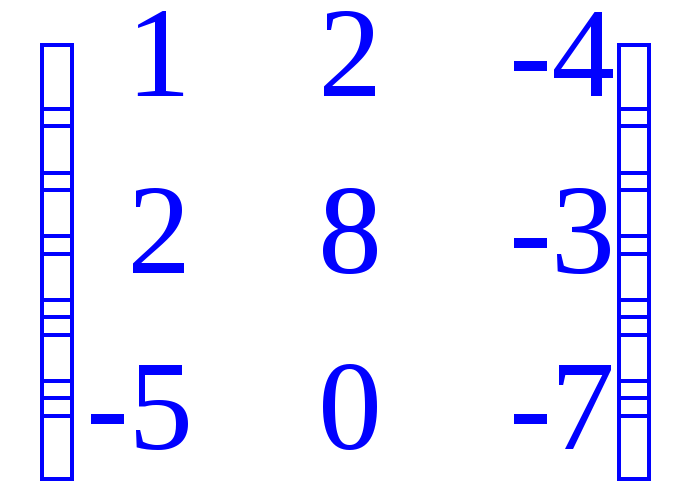
> det(A);#Нахождение определителя матрицы;
> rank(A);# Нахождение ранга матрицы;
> trace(A);# Нахождение следа матрицы;
> norm(B);# Норма матрицы;
> kernel(B); # Ядро матрицы;
Спектральный анализ матрицы:
> evalf(eigenvalues(B,C)); # Собственные числа матрицы;
> evalm(C);
> evalf(eigenvectors(B)); # собственные числа + их кратности + собственные вектора;
> evalf(eigenvals(B,C));
> evalm(C);
> charpoly(A,lambda); # Характеристический многочлен матрицы ;
> charmat(A,lambda); # Характеристическая матрица ;
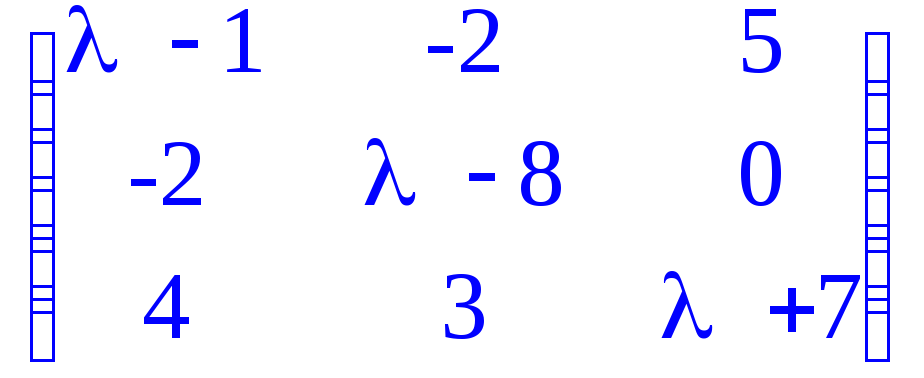
> minpoly(A,lambda); # Минимальный многочлен (делитель) матрицы;
> jordan(A);# Жорданова форма матрицы;
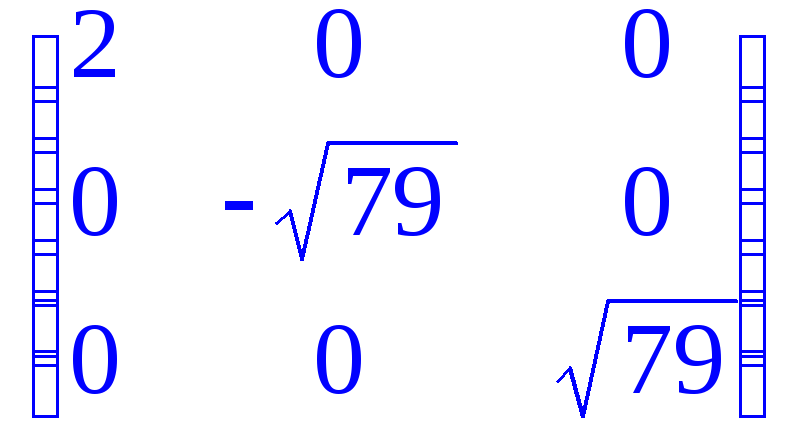
> gausselim(A); # Приведение матрицы к треугольному виду методом Гаусса;
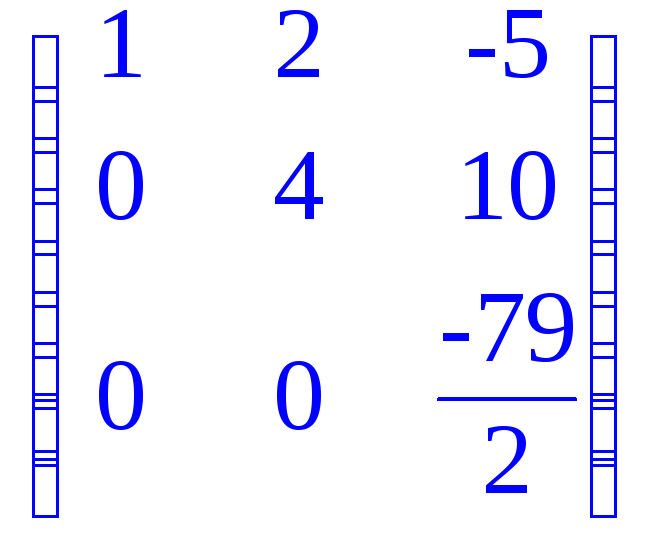
> gaussjord(A); # Приведение матрицы к треугольному виду методом Гаусса - Жордана;
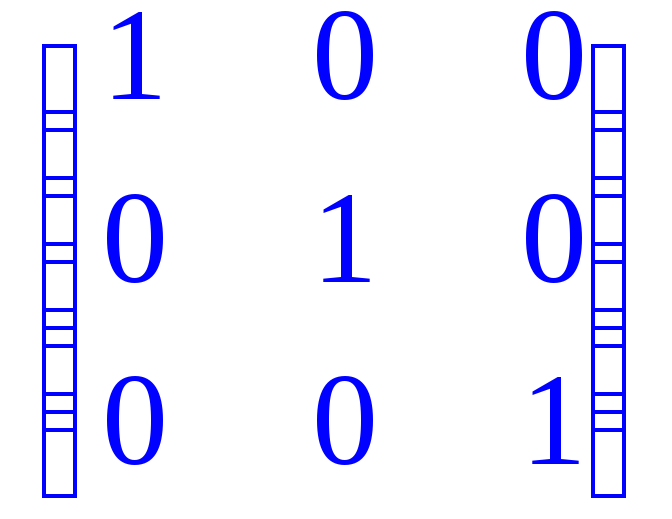
> definite(B,'positive_def'); # Определение положительной определенности матрицы (да - true,нет - false);
Символьные операции с матрицами:
> restart: with(linalg):
Warning, the protected names norm and trace have been redefined and unprotected
> M1:=array(1..2,1..2,[[a1,b1],[c1,d1]]);
> M2:=array(1..2,1..2,[[a2,b2],[c2,d2]]);
> evalm(M1+M2);
> evalm(M1/M2);
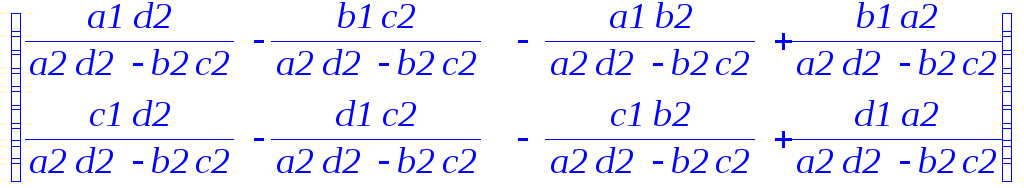
> evalm(M1^2);
> evalm(sin(M1));
> evalm(M1+z);
> M3:=array(1..2,1..2,[[x,x^2],[x^3,x^4]]);
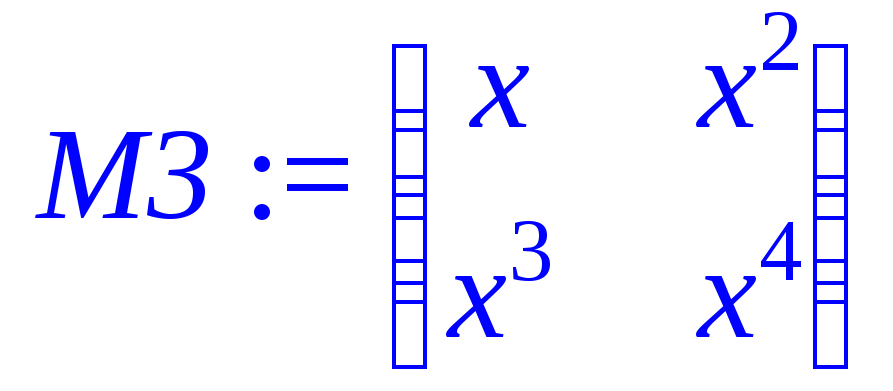
> map(diff,M3,x);# Функция map - применяет заданную операцию к каждому элементу матрицы;
> map(int,%,x);
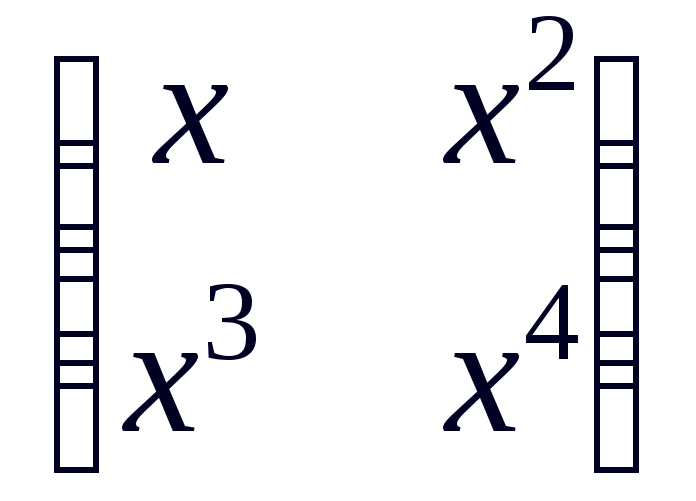
> map(sin,M3);
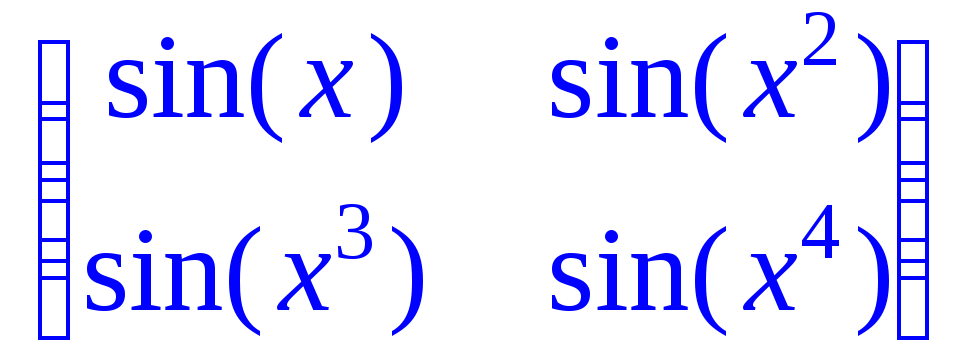
> # Генерация функциональной матрицы;
> f[1]:=(i,j)->x^i+y^j;
> AA:=matrix(2,3,f[1]);
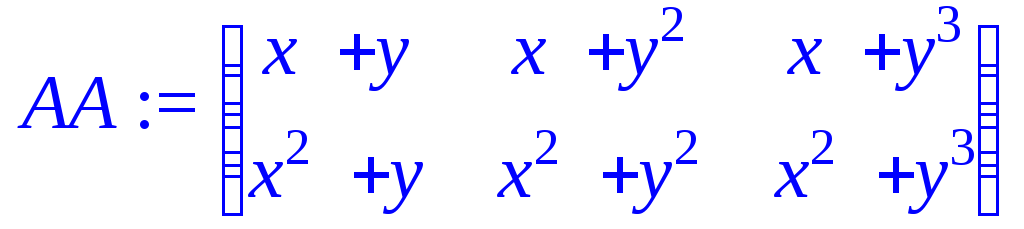
> restart:
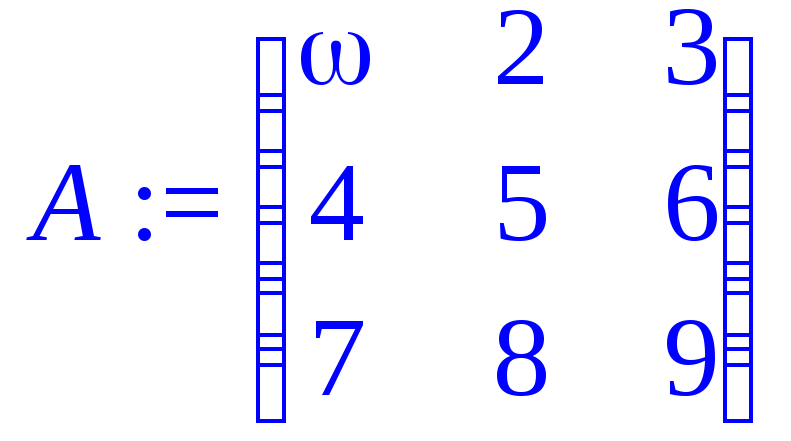
> A:=Matrix(3,3,[[omega,2,3],[4,5,6],[7,8,9]],readonly=true);
> omega:=1:
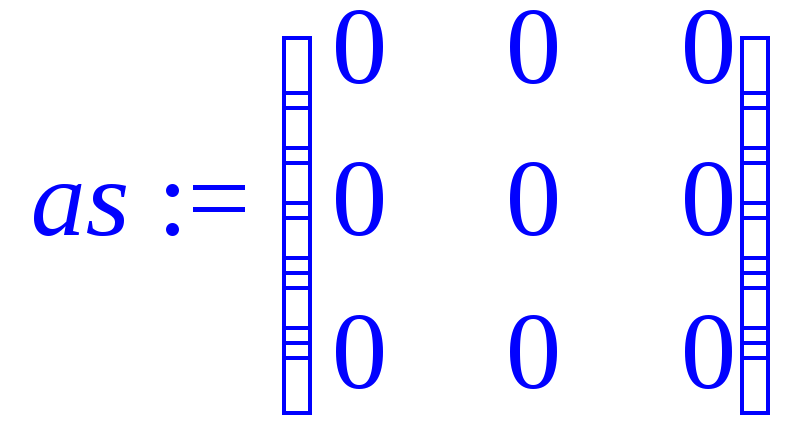
> as:=Matrix(3,3,readonly=false);
> as:=A;
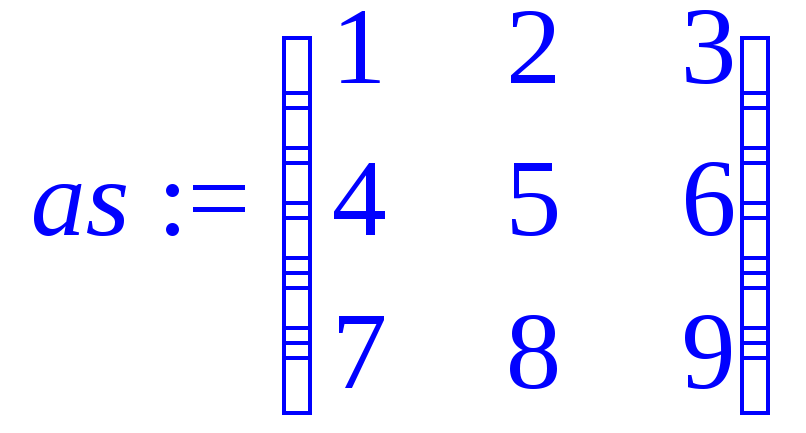
> omega:=2:
> print(as);
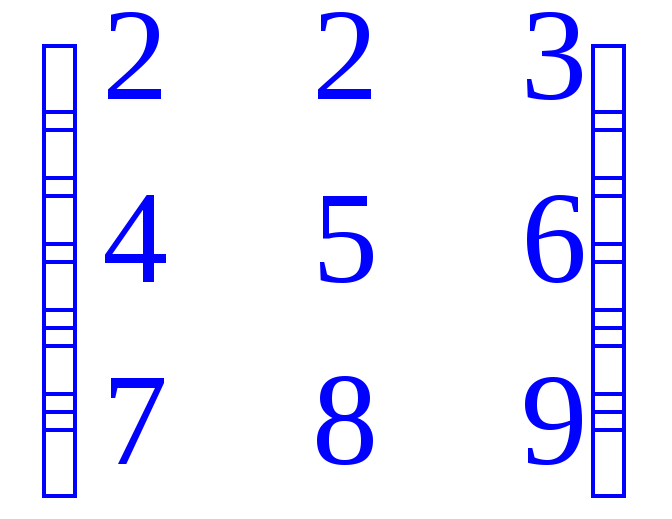
> restart:
> a:=(omega)->matrix(2,2,[[12,omega],[43,566]]);
> a(23);
Решение систем линейных уравнений С*X=B:
> restart:with(linalg):
Warning, the protected names norm and trace have been redefined and unprotected
> C:=matrix(3,3,[[4,8,2],[6,2,3],[3,7,11]]);
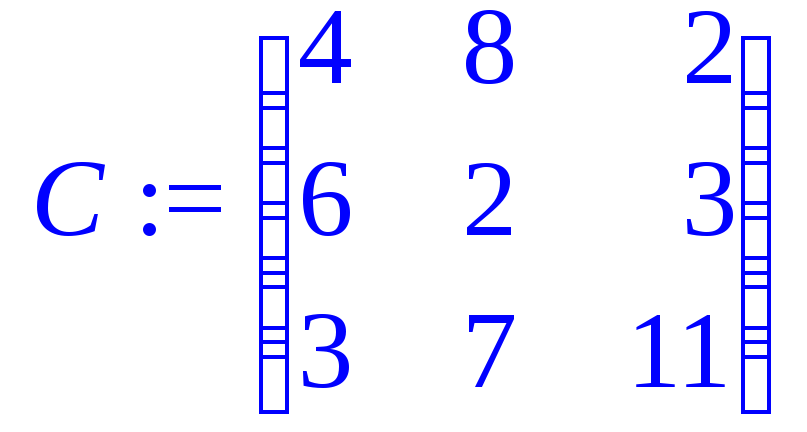
> B:=matrix(3,1,[5,6,1]);
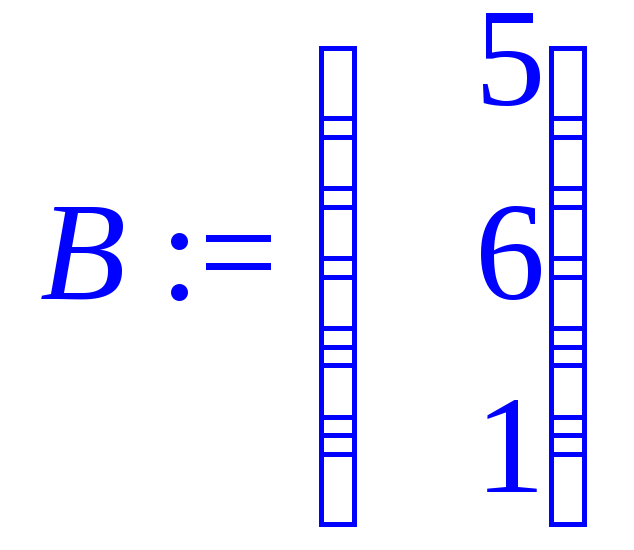
> X:=matrix(3,1);
> X:=evalm((C^(-1))*B);# Первый способ;
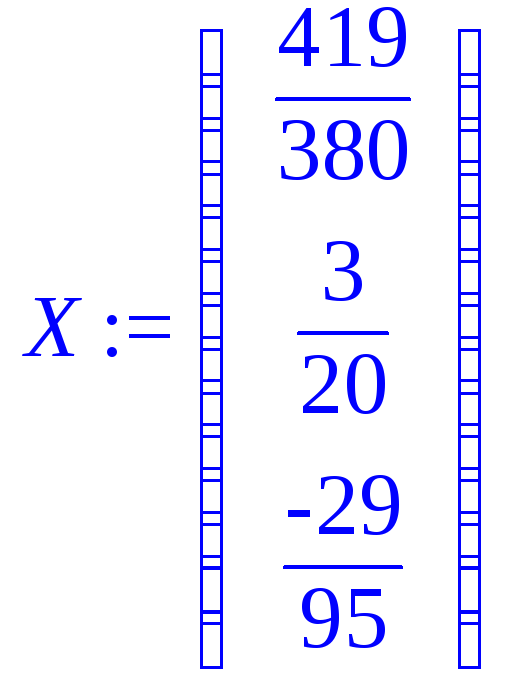
> X:=multiply(inverse(C),B); # Второй способ;
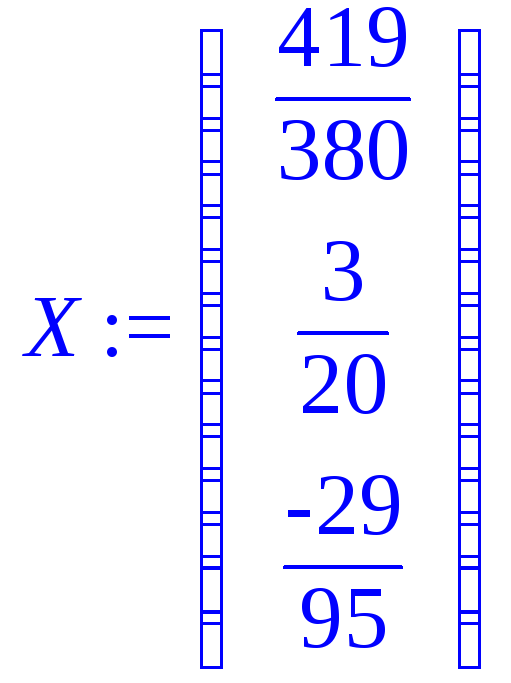
> X:=linsolve(C,B); # Третий способ;
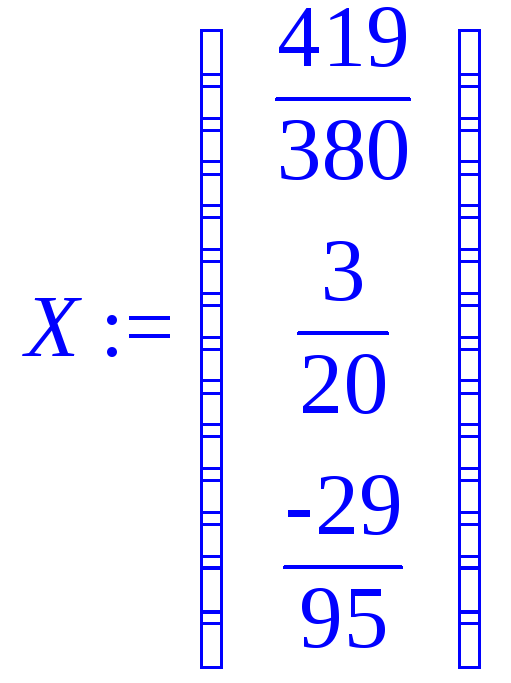
> # Интерактивный ввод матрицы;
> restart;
> with(linalg):
Warning, the protected names norm and trace have been redefined and unprotected
> #A:=array(1..3,1..3);
> #entermatrix(A);
> 1;
> 3;
> 2;
> 5;
> 7;
> 5;
> 2;
> 5;
> 9;
>