2.4 Обработка результатов косвенных измерений

Достаточно часто измеряется не непосредственно искомая величина, а величина (величины), связанная с искомой известным соотношением (зависимостью). Такие измерения называют косвенными. Возможны два основных варианта соотношений между искомой величиной и измеряемой (измеряемыми):

• искомая величина зависит от одной измеряемой величины;

• искомая величина зависит от нескольких измеряемых величин.

Общие правила вычисления погрешностей для обоих случаев можно легко получить с помощью дифференциального исчисления.

В первом случае, если y = f(x), аx - измеряемая величина, то абсолютнуюDy и относительнуюdупогрешности определенияyможно найти из выражений:

(2.16)

где - производная от функции f(x) по переменной х;

Dx - абсолютная погрешность измеренияx.

Во втором случае искомая величина yзависит отn измеряемых величинх₁, х₂,..., х_n: то есть:

. y = f (х₁, х₂, ..., х_n) . Относительная погрешность определения искомой величины в этом случае составит:

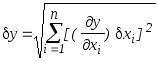, (2.17)

где - частная производная от функцииy = f (х₁, х₂, ..., х_n) по переменнойх_i ;

dх_i- относительная погрешность измерениях_i.

2.5 Обработка результатов измерений (правила округления)

Результат измерений выражается числом, содержащим значащие цифры, количество которых определяется свойствами отсчетного устройства измерительного прибора. Значащими считаются все цифры в числовом результате, в том числе и нуль, если он стоит в середине или конце числа. Например, результаты измерений 1,27^· 10^-2 и 0,0127 содержат по три, а 127,05 и 1275,0 - по пять значащих цифр.

Результат измерений является приближенным значением , содержащим некоторое количество верных знаков. Верными являются все знаки в числовом результате, достоверность которых не вызывает сомнений. Количество верных знаков в результате определяется его погрешностью.

При определении результата измерений следует использовать следующие правила:

а) величина случайной погрешности , как и сам результат измерений, является случайной величиной. Можно показать, что прип= 10 измеренияхопределяется с погрешностью около 30%, прип= 25 - около 15%. Это означает, что прип= 10 измерениях дляследует приводить 1 значащую цифру, если она больше 3, и две значащие цифры, если первая из них меньше 4. Прип= 25...40 измерениях дляследует две значащие цифры.

Пример. Если в результате расчета получено = 0,124, то прип= 10 погрешность измерения принимается равной= 0,1, а прип= 25...40 равной=.0,12. Если в результате расчета получено= 0,437, то погрешность измерения принимается равной= 0,44 в обоих случаях;

б) числовое значение результата измерений (в том числе и результат расчета при косвенных измерениях) должно оканчиваться цифрой того же десятичного знака, что и значение погрешности. Пример. Результат (123,456 ±0,1) мкА следует записать как (123,5±0,1) мкА.

При округлении числового значения результата измерений следует придерживаться следующих правил: