Примеры расчета

Прямоугольные сечения

Пример 2. Дано: сечение размером b = 300 мм, h = 600 мм; а= =40 мм; изгибающий момент с учетом кратковременных нагрузок М = =200 кН^.м; бетон класса В15 (R_b = 8,5 МПа); арматура класса А300 (R_s = 270 МПа).

Требуется определить площадь сечения продольной арматуры.

Р а с ч е т. h₀ = 600 – 40 = 560 мм. Подбор продольной арматуры производим согласно п. 3.21. По формуле (3.22) вычисляем значение _т:

По табл. 3.2. находим _R = 0,41. Так как _т = 0,25 < _R, сжатая арматура по расчету не требуется.

Требуемую площадь сечения растянутой арматуры определяем по формуле (3.23)

мм².

Принимаем 228 + 125 (А_s = 1598 мм²).

Пример 3. Дано: сечение размерами b = 300 мм, h = 800 мм; а = 70 мм; растянутая арматура А400 (R_s = 355 МПа); площадь ее сечения A_s = 2945 мм² (625); бетон класса В25 (R_b = 14,5 МПа); изгибающий момент М = 550 кН^.м.

Требуется проверить прочность сечения.

Р а с ч е т. h₀ = 800 – 70 = 730. Проверку прочности производим согласно п. 3.20:

Определим значение х:

мм.

По табл. 3.2 находим _R = 0,531. Так как , проверяем условие (3.20):

R_s A_s(h₀ – 0,5x) = 355 ^.2945 (730 – 0,5 ^. 240) = 636,8 ^. 10⁶ Н^. мм =636,8 кН^.м > М = 550 кН^.м,

т.е. прочность сечения обеспечена.

Пример 4. Дано: сечение размерами b= 300 мм, h = 800 мм; a = =50 мм; арматура класса А400 (R_s = R_sc = 355 МПа); изгибающий момент M = 780 кН^.м; бетон класса В15 ( R_b = 8,5 МПа).

Требуется определить площадь сечения продольной арматуры.

Р а с ч е т. h₀ = h – a = 800 – 50 =750 мм. Требуемую площадь продольной арматуры определяем согласно п. 3.21. По формуле (3.22) находим значение _т:

Так как _m = 0,544 > _R = 0,39 (см. табл. 3.2), при заданных размерах сечения и класса бетона необходима сжатая арматура.

Принимая а = 30 мм и _R = 0,531 (см. табл. 3.2) по формулам (3.24) и (3.25) определим необходимую площадь сечений сжатой и растянутой арматуры:

мм²;

мм².

Принимаем = 942 мм² (320); A_s = 4021 мм² (532).

Пример 5. Дано: сечение размерами b = 300 мм, h = 700 мм; a = 50 мм; a’ = 30 мм; бетон класса В30 (R_b = 17 МПа); арматура А400 (R_s= R_sc = 355 МПа); площадь сечения сжатой арматуры = 942 мм² (320); изгибающий момент М = 580 кН^.м.

Требуется определить площадь сечения растянутой арматуры.

Р а с ч е т. h₀ = 700 – 50 = 650 мм. Расчет производим с учетом наличия сжатой арматуры согласно п. 3.22.

Вычисляем значение _т:

.

Так как _m = 0,173 < _R = 0,39 (см. табл. 3.2), необходимую площадь растянутой арматуры определяем по формуле (3.26)

Принимаем 336 (A_s = 3054 мм²).

Пример 6. Дано: сечение размерами b = 300 мм, h = 700 мм; a = 70 мм; a’ = 30 мм; бетон класса В20 (R_b = 11,5 МПа); арматура класса А400 (R_s = R_sc= 355 МПа); площадь сечения растянутой арматуры A_s = 4826 мм² (632), сжатой - A= 339 мм² (312); изгибающий момент М = 630 кН^.м.

Требуется проверить прочность сечения.

Р а с ч е т. h₀ = 700 – 70 = 630 мм. Проверку прочности сечения производим согласно п. 3.18.

По формуле (3.16) определяем высоту сжатой зоны х:

мм.

По табл. 3.2 находим _R = 0,531 и _R = 0,39. Так как прочность сечения проверяем из условия (3.18):

т.е. прочность согласно этому условию не обеспечена. Уточним правую часть условия (3.18) путем замены значения _R на (0,7_R + 0,3_m), где

_m = (1 - 0,5) = 0,733(1- 0,5 ^. 0,733) = 0,464:

(0,7 ^. 0,39 + 0,3 ^. 0,464)11,5 ^. 300 ^. 630² + 355 ^. 339 ^. 600 = 636,6 ^. 10⁶ Н^.мм = 636,6 кН^. м > М = 630 кН^.м, т.е. прочность обеспечена.

Тавровые и двутавровые сечения

Пример 7. Дано: сечение размерами = 1500 мм, = 50 мм, b = 200 мм, h = 400 мм; а = 80 мм; бетон класса В25 (R_b = 14,5 МПа), арматура класса А400 (R_s = 355 МПа); изгибающий момент М = 260 кН^.м.

Требуется определить площадь сечения продольной арматуры.

Р а с ч е т. h₀ = 400 – 80 = 320 мм. Расчет производим согласно п. 3.25 в предположении, что сжатая арматура по расчету не требуется.

Проверим условие (3.32), принимая = 0:

R_bb(h₀ – 0,5) = 14,5 ^. 1500 ^. 50(320 – 0,5 ^. 50) = 320,8 ^. 10⁶ Н^.мм =

= 320,8 кН^.м > М = 260 кН^.м,

т.е. граница сжатой зоны проходит в полке, и расчет производим как для прямоугольного сечения шириной b = = 1500 мм согласно п.3.21.

Вычисляем значение

< _R = 0,39 (см. табл. 3.2),

т.е. сжатая арматура действительно по расчету не требуется.

Площадь сечения растянутой арматуры вычисляем по формуле (3.22)

мм².

Принимаем 428(A_s = 2463 мм²).

Пример 8. Дано: сечение размерами = 400 мм, мм, b = 200 мм, h = 600 мм; а = 65 мм; бетон класса В15 (R_b = 8,5 МПа); арматура класса А400 (R_s = 355 МПа); изгибающий момент М = 270 кН^. м.

Требуется определить площадь сечения растянутой арматуры.

Р а с ч е т. h₀ = 600 – 65 = 535 мм. Расчет производим согласно п. 3.25 в предположении, что сжатая арматура по расчету не требуется.

Так как

R_bb(h₀ – 0,5) = 8,5 ^. 400 ^. 120(535 – 0,5 ^. 120) = 193,8 ^. 10⁶ Н^.мм =

= 193,8 кН^.м < M = 270 кН^.м,

граница сжатой зоны проходит в ребре и площадь сечения растянутой арматуры определим по формуле (3.33), принимая площадь сечения свесов равной мм². Вычисляем значение _m, при = 0

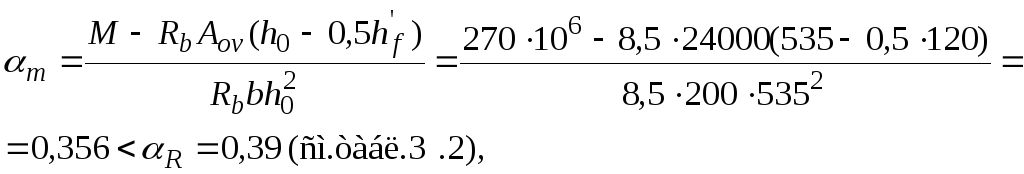
следовательно, сжатая арматура не требуется.

Принимаем 425(A_s = 1964 мм²).

Пример 9. Дано: сечение размерами = 400 мм, = 100 мм, b= 200 мм, h = 600 мм; a = 70 мм, бетон класса В25 (R_b = 14,5 МПа); растянутая арматура класса А400 (R_s = 355 МПа); площадь ее сечения A_s = 1964 мм² (425); = 0,0; изгибающий момент M = 300 кН^.м.

Требуется проверить прочность сечения.

Р а с ч е т. h₀ = 600 – 70 = 530 мм. Проверку прочности производим согласно п. 3.23, принимая = 0,0. Так какR_sA_s = 355 х ^.1964 = 697220 H >R_b=14,5 ^. 400 ^. 100 = 580000 H, граница сжатой зоны проходит в ребре, и прочность сечения проверяем из условия (3.28).

Для этого по формуле (3.29) определим высоту сжатой зоны, приняв площадь свесов равной мм² :

мм < _Rh₀ = 0,531 х ^.530 = 281 мм (где _R найдено из табл. 3.2).

R_bbx (h₀ – 0,5x) + R_bA_ov(h₀ – 0,5h) = 14,5 ^. 200 ^. 140 ^. (530 – 0,5 ^. 140) +

+ 14,5 ^. 20000(530 – 0,5 ^. 100) = 326 ^. 10⁶ Н^.мм = 326 кН^.м>М = 300 кН^.м,

т.е. прочность сечения обеспечена.