Черт.3.6. Тавровое сечение со сжатой зоной, заходящей в наименее растянутый свес полки

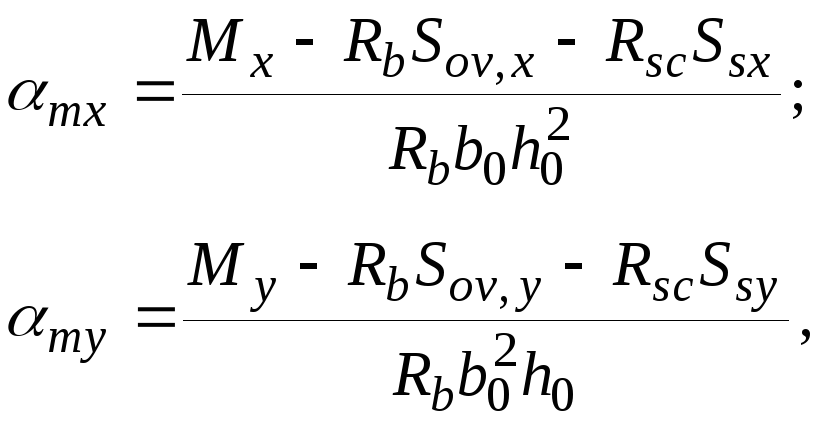
где S_sx и S_sy – статические моменты площади относительно соответственно оси y и оси x.

Остальные обозначения - см. п. 3.27.

Если _mx < 0, расчет производится как для прямоугольного сечения, принимая b = .

Если значение _s на графике находится по левую сторону от кривой, отвечающей параметру , подбор арматуры

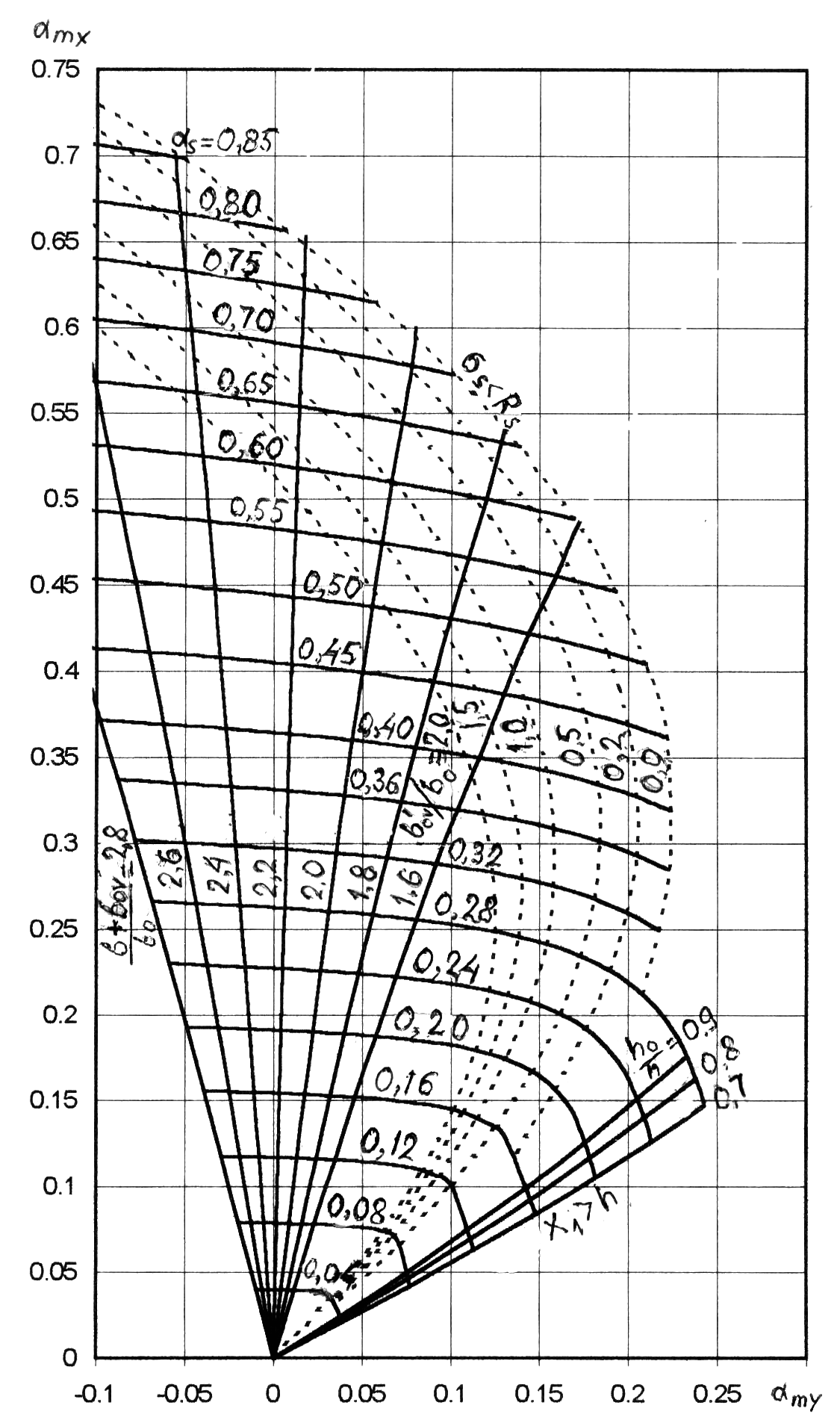
Черт.3.7. График несущей способности прямоугольного, таврового и г-образного сечений для элементов, работающих на косой изгиб

производится без учета косого изгиба, т.е. согласно пп.3.22 и 3.26 на действие момента М = М_х.

Требуемая площадь растянутой арматуры при условии ее работы с полным расчетным сопротивлением определяется по формуле

, (3.42)

где A_ov – см. формулу (3.36).

Центр тяжести фактически принятой растянутой арматуры должен отстоять от растянутой грани не дальше, чем принятый в расчете центр тяжести. В противном случае расчет повторяют, принимая новый центр тяжести сечения растянутой арматуры.

Условием работы растянутой арматуры с полным сопротивлением является выполнение условия (3.40).

При арматуре класса А400 и ниже условие (3.40) всегда выполняется, если значение _s на графике 3.7 находится внутри области, ограниченной осями координат, и кривой, отвечающей параметру .

Если условие (3.40) не выполняется, следует поставить (увеличить) сжатую арматуру, либо повысить класс бетона, либо увеличить размеры сечения (особенно наиболее сжатого свеса полки).

Значения _s на графике не должны находиться между осью _my и кривой, соответствующей параметру h₀ / h. В противном случае х₁ становится более h , и расчет тогда следует производить согласно пп. 3.72-3.76.

Примеры расчета

Пример 10. Дано: железобетонный прогон кровли с уклоном 1:4 (ctg=4); сечение и расположение арматуры – по черт. 3.8; бетон класса В25 (R_b=14,5МПа); растянутая арматура класса А400 (R_s=355МПа); A_s = 763 мм² (318); = 0,0; изгибающий момент в вертикальной плоскостиМ = 82,6 кН^.м.

Требуется проверить прочность сечения.

Р а с ч е т. Из черт. 3.8 следует:

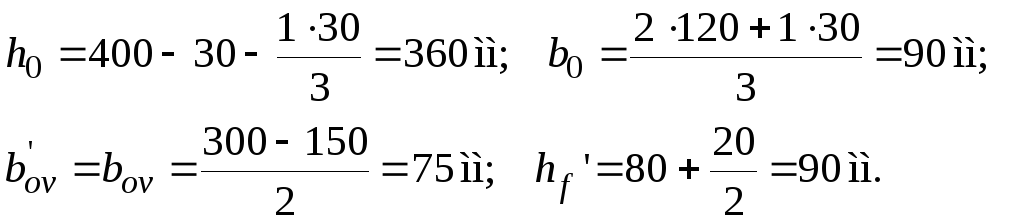
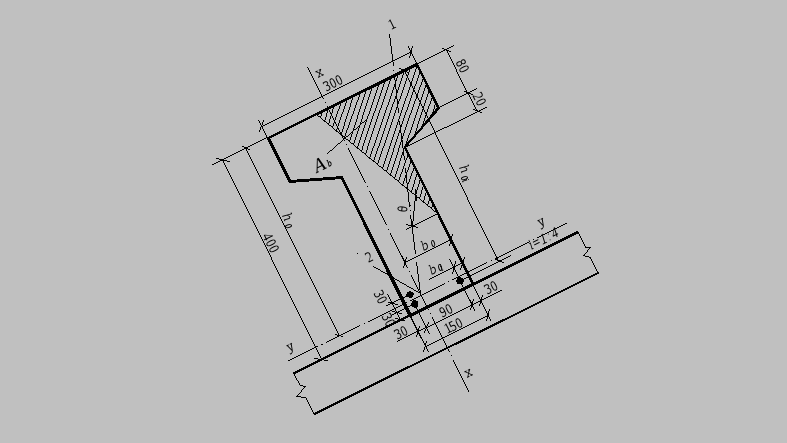
Черт.3.8 к примеру расчета 10

1-плоскость действия изгибающего момента; 2-центр тяжести сечения растянутой арматуры

По формуле (3.37) определим площадь сжатой зоны бетона A_b:

мм².

Площадь наиболее сжатого свеса полки и статические моменты этой площади относительно х и у соответственно равны:

А_ov= = 75 ^. 90 =6750 мм²;

S_ov,y = A_ov(b₀ + b/2)=6750(90 + 75/2) = 86,06 ^. 10⁴ мм³;

S_ov,x= A_ov(h₀ - /2) = 6750(360 – 90/2) = 212,6 ^. 10⁴ мм³.

Так как A_b > A_ov, расчет продолжаем как для таврового сечения.

A_web = A_b – A _ov = 18680 – 6750 = 11930 мм².

Определим по формуле (3.38) размер сжатой зоны х₁. Для этого вычисляем

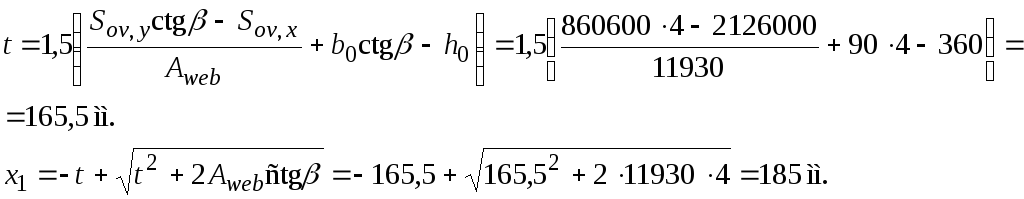
Проверим условие (3.39):

мм < x₁ = 185 мм,

cледовательно, расчет продолжаем по формулам косого изгиба.

Проверим условие (3.40) для наименее растянутого стержня. Из черт. 3.8 имеем b_0i= 30 мм, h_0i = 400 – 30 = 370 мм;

(см. табл. 3.2).

Условие (3.40) не соблюдается. Расчет повторим, заменяя в формуле (3.37) значение R_s для наименее растянутого стержня напряжением _s, определенным по формуле (3.41), и корректируя значения h₀ и b₀.

МПа =

=0,945 R_s.

Поскольку все стержни одинакового диаметра, новые значения A_b,b₀ и h₀ будут равны:

Аналогично определим значения S_ov,y, S_ov,x, A_web и x₁:

S_ov,y = 6750(91,1 + 75/2 = 86,8 ^. 10⁴ мм³;

S_ov,x = 6750(359,8 – 90/2) = 212,5 ^. 10⁴ мм³;

A_web = 18338 – 6750 = 11588 мм²;

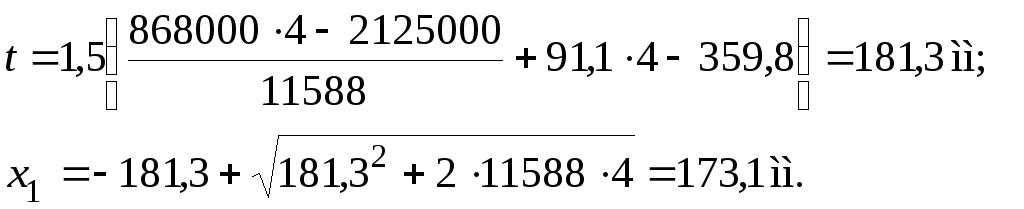
Проверяем прочность сечения из условия (3.35), принимая S_sx =0 и кН^.м:

R_b[A_web(h₀ – x₁/3) +S_ov,x] = 14,5[11588(359,8 – 173,1/3) + 212,5 ^. 10⁴] =

=81,57 ^. 10⁶ Н^.мм> M_x = 80,1 ^.10⁶ Н^.мм,

т.е. прочность сечения обеспечена.

Пример 11. По данным примера 10 необходимо подобрать площадь растянутой арматуры при моменте в вертикальной плоскости М = 64 кН^.м.

Р а с ч е т. Составляющие изгибающего момента в плоскости осей у и х равны:

кН^.м;

M_x = M_y сtg = 15,52 ^. 4 = 62,1 кН^.м.

Определим необходимое количество арматуры согласно п. 3.28.

Принимая значения R_b, h₀, S_ov,x и S_ov,y из примера 10 при S_sy = S_sx= 0 находим значения _mx и _my:

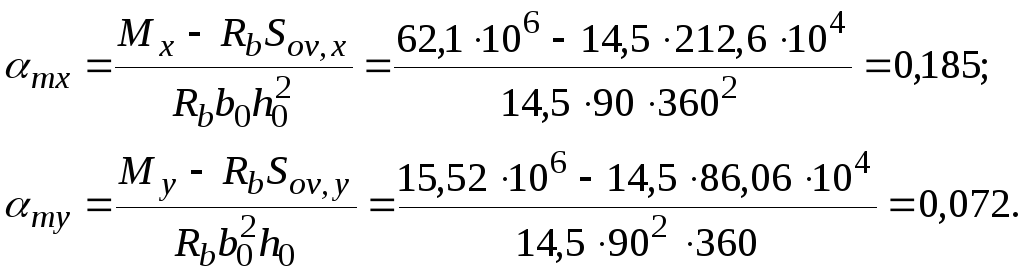
Так как _mx> 0, расчет продолжаем для таврового сечения.

Поскольку точка с координатами _mx = 0,185 и _my = 0,072 на графике черт. 3.7 находится по правую сторону от кривой, отвечающей параметру , и по левую сторону от кривой, отвечающей параметру, расчет продолжаем с учетом косого изгиба и полного расчетного сопротивления арматуры, т.е. условие (3.40) выполнено.

На графике координатам _mx = 0,185 и _my = 0,072 соответствует значение _s = 0,20. Тогда согласно формуле (3.42) площадь сечения растянутой арматуры будет равна

A_s = (_sb₀h₀ + A_ov)R_b/R_s = (0,2 ^. 90 ^. 360 + 6750)14,5/355 = 540,4 мм².

Принимаем стержни 316 (A_s = 603 мм²) и располагаем их, как показано на черт. 3.8.