Порядок выполнения работы

1. Собрать электрическую схему установки (см. рис. 15.1 и 15.4).

2. Установить анодное напряжение В по вольтметру ИП.

3. Изменяя ток в соленоиде от минимального (начального) значения до максимального через 0,1 А при постоянном анодном напряжении, снять сбросовую характеристику, т.е. зависимость анодного тока от тока в соленоиде. Значения анодного тока, определяемые по прибору РА, и значения тока в соленоиде определяемые по показаниям амперметра ИП, занести в табл. 15.1.

4. Повторить пп. 2 и 3 при двух других значениях анодного напряжения (больших 50 В). Результаты измерений занести в табл. 15.1.

Т а б л и ц а 15.1

5. Для каждого значения анодного напряжения построить сбросовую характеристику, откладывая по оси ординат значения анодного тока, а по оси абсцисс - значения тока в соленоиде. Для нахождения критического значения тока в соленоиде провести до взаимного пересечения касательную к точке перегиба сбросовой характеристики (на участке ее спада) и прямую, соответствующую изменению минимальных значений анодного тока (как показано на рис. 15.5). Занести полученные значенияв табл. 15.2.

Т а б л и ц а 15.2

е/m

Рис. 15.4

Рис. 15.5

6. Для каждого критического значения тока в соленоиде рассчитать по формуле (15.10) индукцию магнитного поля. Величины 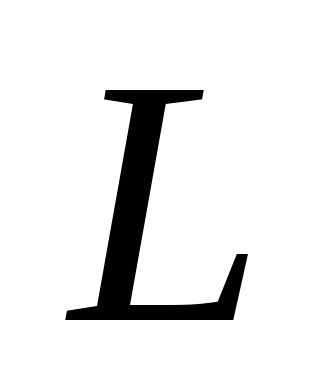,D, N, r_a и r_к принять равными: =167 мм,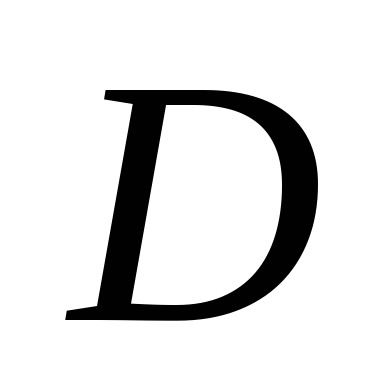=62 мм,N =2108, r_a = 6 мм, r_к = 0,3 м.

7. Вычислить по формуле (15.9) для каждого значения критического поля в соленоиде и определить ее среднее значение.

8. Вычислить погрешность полученной величины .

Контрольные вопросы

1. В чем суть метода магнетрона для определения отношения ?

2. Влияет ли на величину изменение направления тока в соленоиде на противоположное?

3. Зависит ли величина от величины анодного напряжения?

4. Рассмотреть движение электрона в однородном магнитном поле в двух случаях: а) скорость электрона ; б) скорость электронанаправлена под угломк полю.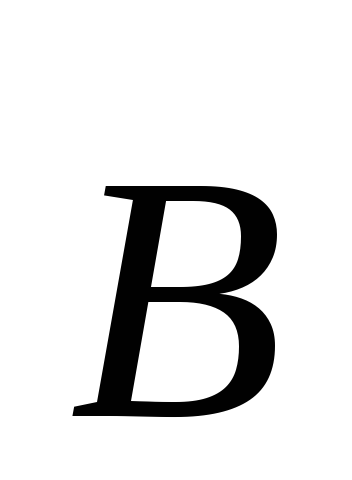

Библиогр.: [1,4,5].

Лабораторная работа № 16

Изучение магнитного поля соленоида

с помощью датчика Холла

Цель работы – познакомиться с холловским методом измерения индукции магнитного поля.

Краткие сведения из теории

В пространстве, окружающем проводники с током или движущиеся заряды, возникает магнитное поле, которое можно обнаружить по воздействию его на другой проводник с током или на магнитную стрелку. Магнитное поле в каждой точке пространства количественно может быть описано с помощью вектора напряженности или вектора индукциимагнитного поля. В вакууме векторыисвязаны соотношением

(16.1)

где – магнитная постоянная.

Для вычисления напряженности и индукции магнитного поля используют закон Био – Савара – Лапласа, согласно которому элементарная напряженность магнитного поля , создаваемая элементом проводникас силой токав некоторой точке пространства на расстоянии, определяется выражением

(16.2)

Для нахождения результирующей напряженности, создаваемой проводником конечных размеров, надо воспользоваться принципом суперпозиции магнитных полей и найти векторную сумму элементарных напряженностей :

(16.3)

В пределе сумма записывается в виде интеграла по контуру проводника с током. Применим формулу (16.3) для вычисления напряженности магнитного поля на оси соленоида. Каждый виток соленоида – это круговой ток, поэтому первоначально вычислим напряженность поля на оси кругового витка с током (рис. 16.1). При сложении составляющих магнитного поля перпендикулярных осиОА, они компенсируют друг друга вследствие симметрии контура. Поэтому результирующая напряженность магнитного поля в точке А направлена вдоль оси кругового тока и равна по модулю:

; (16.4)

. (16.5)

В (16.5) учтено, что векторы и взаимно перпендикулярны. Подставив (16.5) в (16.4) и учитывая, что величиныJ, ипостоянны, получим

(16.6)

Перейдем теперь к вычислению поля соленоида, изображенного на рис. 16.2. Пусть на единицу длины соленоида приходится п витков, тогда на участке dz будет ndz витков, которые в точке 0 соленоида согласно (16.6) создадут напряженность

(16.7)

На рис. 16.3 отдельно изображены элемент dz, радиус-вектор и углы и . Из геометрических построений рис. 16.2 и 16.3 следует:

. (16.8)

Рис. 16.2

Рис. 16.3

Подставляем (16.8) в (16.7) и интегрируем в пределах от до :

(16.9)

В случае бесконечного соленоида

(16.10)