Задание 2. Исследование фазовых кривых

Для наблюдения на экране фазовой кривой на вертикально отклоняющие пластины осциллографа подают напряжение с обкладок конденсатора, а на горизонтально отклоняющие пластины – напряжение с клемм магазина сопротивлений, пропорциональное току. Таким образом, на экране осциллографа изображается зависимость напряжения на обкладках конденсатора от тока I в контуре.

1. Включить осциллограф. Получить на экране фазовую кривую (см. рис. 20.4).

2. Установить картину в центре экрана.

3. Вращая ручку магазина сопротивлений, получить фазовые кривые при различных сопротивлениях.

4. Измерить значения напряжения, разделенные периодом колебаний, т.е. расстояния от центра фазовой кривой до точки пересечения витков спирали с осью напряжения и вычислить логарифмический декремент затухания:

Аналогичным образом вычислить логарифмический декремент по значениям силы тока I, измеренным через период колебаний:

Измерения выполнить по всем виткам фазовой кривой. Результат записать в табл. 20.2.

Т а б л и ц а 20.2

Rм	R=Rк+Rм	U10	U20	U30	λ	I10	I20	I30	λ

5. Повторить измерения п. 4 при значениях сопротивления магазина 100, 200, 300, 400, 500, 600 0м.

6. Зарисовать фазовую кривую при апериодическом разряде конденсатора.

7. Рассчитать погрешность определения :

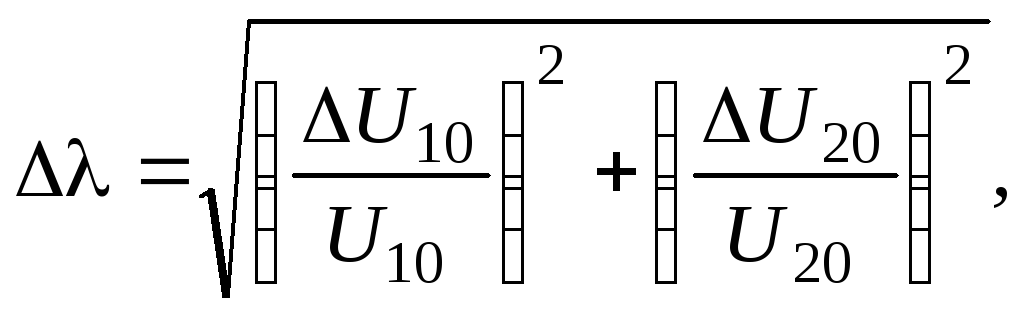
где – погрешность измеренияна экране.

Контрольные вопросы

1. Что такое колебательный контур, и как в нем возникают колебания?

2. Что такое логарифмический декремент затухания?

3. Что представляет собой апериодический разряд в контуре, и при каких условиях он происходит?

4. Что такое фазовая плоскость и фазовая кривая?

5. Какова форма фазовой кривой: а) при незатухающих колебаниях; б) при затухающих колебаниях; в) при апериодическом разряде?

Библиогр.: [1, 2, 11].

Лабораторная работа №21 Изучение вынужденных колебаний в колебательном контуре

Цель работы – изучить зависимость силы тока в колебательном контуре от частоты источника ЭДС, включенного в контур, и измерить резонансную частоту контура.

Краткие сведения из теории

Рассмотрим процессы, протекающие в колебательном контуре, подключенном к источнику, ЭДС которого изменяется по гармоническому закону:

(21.1)

где – напряжение на конденсаторе емкостьюС; I – ток в контуре.

П

Рис. 21.1

олагаем, что мгновенные значения токов и напряжений удовлетворяют законам, установленным для цепей постоянного тока. Такие токи называют квазистационарными. В любой момент времени сумма падений напряжения на элементах цепи равна ЭДС (рис. 21.1):

. (21.2)

Падение напряжения на катушке индуктивностью L

(21.3)

ток в катушке и в контуре

(21.4)

Подстановка (21.3) и (21.4) в (21.2) дает

(21.5)

Разделим это уравнение на LC и введем обозначения:

Обозначая дифференцирование по времени точкой, получим дифференциальное уравнение

(21.6)

Его решение дает закон изменения напряжения на конденсаторе с течением времени и равно сумме общего решения однородного уравнения (21.7) и частного решения неоднородного уравнения (21.6):

(21.7)

Однородное уравнение (21.7) имеет решение

(21.8)

являющееся уравнением затухающих колебаний (см. лабораторную работу №19). Затухание определяется членом За времяамплитуда колебаний уменьшится ве раз. Затухание в колебательном контуре связано с превращением анергии колебаний в джоулево тепло на сопротивлении . При составляющей решения (21.6) (она отражает переходный процесс, определенный начальными условиями и параметрами контура) обычно пренебрегают, так как она становится весьма малой по сравнению с частным решением вышеупомянутого уравнения. Последнее можно представить в следующем виде:

, (21.9)

где иопределяются путем подстановки (21.9) в (21.6). В результате получаются следующие равенства:

(21.10)

(21.11)

Таким образом, установившиеся колебания в цепи происходят с частотой и сдвигом по фазепричем амплитуда и фаза напряжения на конденсаторе зависят от соотношения частоты источника ЭДСи частоты.

Ток в контуре

где . Амплитуда тока в контуре также зависит от соотношения частоти

(21.12)

График зависимости отпредставлен на рис. 21.2.

Из графика видно, что амплитуда силы тока резко возрастает при приближении циклической частоты источника ЭДС к частоте. Это явление называется резонансом, а кривые – резонансными кривыми. Величина максимума зависит от: при(кривая3); при увеличении максимальное значениеуменьшается (кривые2 и 1), определяет разность фаз колебаний тока в контуре и внешней ЭДС:

(21.13)

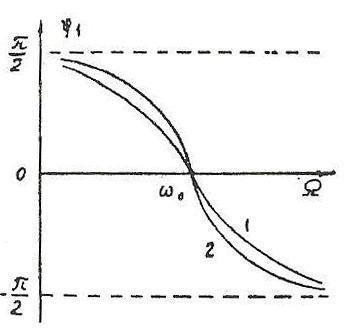
Рис. 21.2 Рис. 21.3

График зависимости от частоты представлен на рис. 21.3. Кривые 1 и 2 соответствуют разным значениям . Прии. Величинагденазывается добротностью колебательного контура. Добротность контура связана с остротой резонансных кривых. Найдем ширину резонансной кривой (рис. 21.4) приИз формулы (21.12) следует, что максимальное значение силы тока

,

а

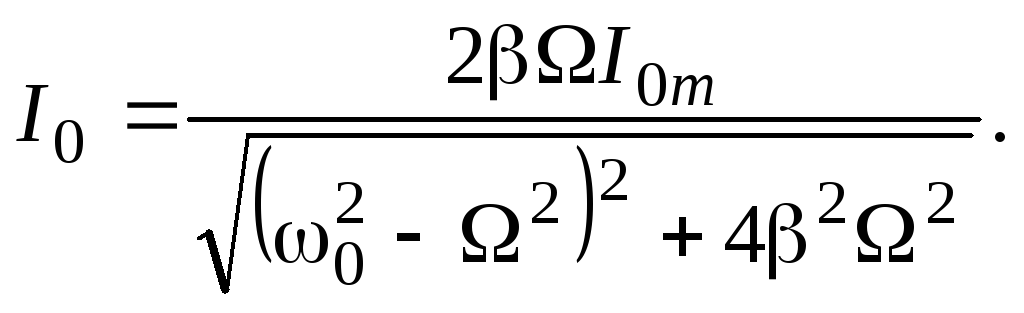(21.14)

При из (21.14) следует равенство

(21.15)

Выражение (21.15) можно преобразовать к виду или. В последнем равенстве (полученном при) величина(обозначена на рис. 21.4), и вблизи резонансной частоты можно положить. Отсюдаи

(21.16)

Рис. 21.4

При малом затухании и. Тогда

(21.16а)

т.е. относительная ширина резонансной кривой численно равна обратной величине добротности контура.

Таким образом, в этом случае добротность может быть рассчитана по формуле

(21.16б)