24 Особенности симметричных и ассиметрич. Систем шифрования данных
По назначению использ. ключа. криптогр. системы дел. на:
1) симметричн. В прям. и обратн. преобраз. (зашифр./ расшифр.) используется одинак. ключ. Ключ является тайным. Алгоритм известен.
Например пусть используется симметричный блочный алгоритм, длина блока 4 символа. Алгоритм преобразования основывается на вычислении по mod 2, расшифрование тоже.
М = 10101100
К = 0101 (тайная информация) Т.к. длина блока 4, то К тоже 4.
Зашифрование:
Сообщение М делим на блоки в соотв. С принятой длиной m1 = 1010, m2 = 1100.
C = f (алгоритм, К, М) – шифртекст (шифрограмма), справедливо для любой криптограф. системы.
При использовании блочного алгоритма шифрования текста С = с1…сl
В нашем случае С= с1с2
с1 = m1 + К = 1010+0101=1111 (+ это сложение по mod 2).
с2 = m2 + К = 1100+0101=1001
С = 11111001 такой шифртекст по открытым каналам поступает к получателю.
Обратное преобразование (расшифрование):
M’ = f (C, K, алгоритм)
M’ = m1’m2’
m1’ = c1 + K = 1111+0101=1010= m1
m2’ = c2 + K = 1001+0101=1100= m2
M’ = 10101100 = M
В реальн. системах помимо вычислит. операций исп-ся множествен. подстановки и перестановки. Наи> известн. и 1 из стандартизован. — стандарт. DES, принят в США и позднее исп-ся во всем мире. Длина ключа = 64 bit из кот. 54 вычислительных, 8 — биты чётности (CRC). Особ-ти этой системы: 1) хранение/ обмен ключами; 2) «+» сравнит-но не > длина ключа; вычисл. производ-ся быстрее, т.к. не > длина ключа; 3) «-» при < длине ключа проще его найти хотя бы методом простого перебора.
2) асимметр. Системы предполагают, что при прям. и обратн. преобраз. исп-ся различн. ключи, взаимосвязан. м-у собой по известн. законам. Известный метод RSA.
Криптографическая система шифрования данных RSA (1978 г.) является одной из первых практически реализованных идей Диффи и Хеллмана. RSA предполагает, что каждый пользователь независимо от других пользователей генерирует свои собственные ключи (тайный и публичный): тайный известен только пользователям, публичный – общедоступен.
В
RSA
n
представляет собой составное число
,
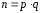числаp
и q –
большие целые простые (примерно одного
порядка), n –
открытое число, p
и q –
тайные.
Задача злоумышленника – разложить n (известное) на простые сомножители.
Система предполаг., что кажд. пользователь может независ. создать свой ключ.
Математической основой системы является теорема:
Для
целых чисел e
и d,
удовлетворяющих соотношению e*d
mod
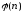=1,
где
1)
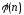(ф-ция Эйлера) иM
(сообщение) должны быть взаимно простыми;
2) должны быть взаимно простыми пары чисел e и n, d и n;
выполняется равенство (M^e mod n) ^d mod n = M.
Процедура генерации (создания) ключа:
1. Выбрать сопоставимые по величине 2 простых числа p и q.
2.
Вычислить
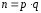(n является
открытым числом).
3.
Вычислить функцию Эйлера [определяет
количество целых положительных чисел,
меньших n
и взаимно простых с n;
n>1;
если n
– простое число, то
;
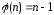если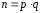
,
гдеp
и q –
простые числа, то
]:
(
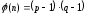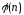является
закрытым числом).
4.
Случайным образом выбирается число e
(или d),
которое должно быть взаимно простым с
.
5. Вычисляется мультипликативное инверсное значение к величине, определенной в п. 4 в соответствии со следующими формулами:
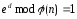
Если
в п. 4 выбрано e,
то в п. 5 используют соотношение:
.
Принято считать, что пара (e,n) – открытый ключ пользователя, а число d – закрытый ключ (d,n).
Пример1: 1. Пусть p = 3, q = 7.
2.
Тогда
.
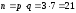3.
Вычисляем
.
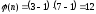4. Выбираем e = 17 (взаимно простое с 12).
5.
Решаем уравнение
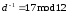или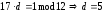
.
Открытый ключ: (17,21); закрытый: (5) или (5,21).
А отправляет сообщение В. Используются ключи получателя В и при зашифровании и при расшифровании. e и n – общедоступны и находятся на специализированных сайтах.
Действия
А:
1.
Создание шифр-текста:
.
Если
М поделено на блоки одинаковой длины
(m1,
m2,
…, mL),
то С = с1,
с2,
…, сL,
где
.
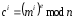2. Отправка на адрес В шифр-текста С.
Действия В: 1. Получение: С = с1, с2, …, сL.
2.
Расшифрование:
В использует соответствующий тайный ключ d.
Если
сообщение разделено на блоки:
.
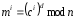Пример2: Открытый ключ: (17,21); закрытый: (5,21). Предполагается, что сообщение М состоит из 5 символов.
Сообщение М делится на блоки одинаковой длины по одному символу.
Пусть М = 12345 и m1 = 01, m2 = 02, …, m5 = 05.
Процедура зашифрования:
,
,
,
,
.
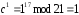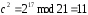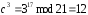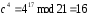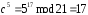Шифр-текст: С = 01 11 12 16 17.
Процедура расшифрования:
,
,
,
,
.
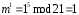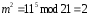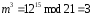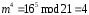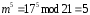Имеем: М = 12345.