Ксилометрический способ применим также и при определении объема сеянцев, листьев, семян, хвои, корней и т. п., для чего необходимо использовать ксилометр с небольшой площадью поперечного сечения.
Гидростатический, или весовой, способ. Так как вес 1 л или 1 дм3
воды при t = 4°C равен одному килограмму, то разность весов тела в воздухе и при погружении в воду, выраженная в килограммах, составит его объем в
дм3. Если взвешивание производилось в тоннах, то разность весов даст объем в м3.
Для весового способа определения объема используются гидростатические весы. Чтобы погрузить древесину в воду, к ней прикрепляют груз (металлический стержень), вес которого устанавливают предварительно. Древесину с грузом взвешивают в воздухе и в воде: разность этих весов, уменьшенная на вес груза, составит объем древесины в дм3. Для наглядного представления, приведем цифровой пример (табл. 6).
Таблица 6
Вес древесины
Показатели |
|
Вес в кг |
|
древесины с гру- |
груза |
древесины |
|
|
зом |
||
|
|
|
|
Вес в воздухе Р |
32,1 |
7,5 |
24,6 |
Вес в воде р |
1,5 |
6,5 |
прибавка 5 |
Потеря веса Р–р |
30,6 |
1,0 |
29,6 |
Следовательно, объем древесины V=Р – р = 29,6 дм3 = 0,0296 м3. Гидростатический способ определения объема древесины в принципе
есть не что иное, как определение удельного веса древесины.
Если известен удельный вес частей дерева, то объем может быть определен по формуле:
P = vδ ; откуда δ = UP или v = Pδ ,
следовательно, объем получается делением веса (Р) на удельный вес(δ) древесины. Но удельный вес древесины – непостоянная величина, зависящая от многих факторов, поэтому, пользуясь даже средними величинами δ, объем древесины по этому способу определяется неточно.
В табл. 13 приводятся удельные веса древесины отдельных пород в зависимости от влажности.
Пример: вес партии воздушно-сухих сосновых дров составил 1,3 тонны. Объем древесины по формуле v = Pδ составит v = l,3 м:0,52 = 2,5 м3.
При определении объема большой партии однородной древесины в целях уточнения результатов прибегают к использованию способа выборки (пробы), объем которой и определяется ксилометрическим способом.
Таблица 7
|
|
Удельный вес древесины, тонна/м3 |
|
||
|
Породы |
Свежесрубленная |
Воздушно-сухая |
||
|
колебания |
средняя |
колебания |
средняя |
|
|
|
||||
Дуб |
|
0,93–1,28 |
1,11 |
0,69–1,03 |
0,76 |
Ясень |
0,70–1,14 |
0,92 |
0,57–0,94 |
0,75 |
|
Береза |
0,80–1,09 |
0,95 |
0,51–0,77 |
0,65 |
|
Сосна обыкно- |
0,38–1,03 |
0,70 |
0,31–0,74 |
0,52 |
|
венная |
|||||
|
|
|
|
||
Лиственница |
0,52–1,00 |
0,81 |
0,44–0,80 |
0,60 |
|
Ель |
0,40–1,07 |
0,74 |
0,35–0,60 |
0,45 |
|
Липа |
0,61–0,87 |
0,74 |
0,32–0,59 |
0,45 |
|
Осина |
0,61–0,99 |
0,80 |
0,43–0,56 |
0,51 |
Объем всей партии v определяется из пропорции: Vv = Pp , откуда V = v ×pP .
Пример: общий вес Р = 1200 кг, вес пробы р = 50 кг. Объем пробы v = 0,1 м3, общий объем древесины:
V = 0,1×1200 = 2,4 м3.
50
Чтобы удельный вес древесины не смешивать с удельным весом вещества, образующего древесину, его принято называть объемным весом. Таким образом, разделив вес древесины Р на объемный вес δ, получаем объем взвешенной древесины V.
Вопрос объемного веса древесины главнейших древесных пород подвергался многочисленным исследованиям, результаты которых обобщены в ГОСТ 3243-46 на дрова для отопления, сухой перегонки и углежжения (табл. 14).
Приемка и учет по весу дров, согласно табл. 8, допускается только в отношении воздушно-сухих дров, причем весовой единицей в таких случаях служит m (1000 кг).
Таблица 8
Удельный вес древесины
|
|
|
|
|
|
Вес плотного м3 здоровой древесины без гнили в кг |
|||
Породы |
при влажности |
при влажности |
в процентах к |
|
весу древесины |
||||
|
25–20% |
50–33% |
||
|
сосны |
|||
|
|
|
||
Граб |
820 |
970 |
156 |
|
Дуб, ясень, |
730 |
860 |
139 |
|
клен |
||||
|
|
|
||
Лиственница |
700 |
820 |
133 |
|
Бук |
680 |
800 |
130 |
|
Береза |
670 |
790 |
128 |
|
Ильм или вяз |
670 |
790 |
128 |
|
Ольха |
540 |
650 |
103 |
|
Сосна |
525 |
625 |
100 |
|
Осина или липа |
500 |
600 |
95 |
|
Ель |
470 |
560 |
90 |
|
Кедр сибир- |
460 |
550 |
88 |
|
ский |
||||
|
|
|
||
Пихта кавказ- |
460 |
550 |
88 |
|
ская |
||||
|
|
|
||
Пихта сибир- |
410 |
490 |
78 |
|
ская |
||||
|
|
|
2.2 Форма древесного ствола. Видовые числа и коэффициенты формы
Форма древесного ствола является наиболее важным объектом исследования в лесной таксации, так как при определенном соотношении диаметра и высоты она обуславливает объем ствола, а также его использование при оценке запаса древостоя.
В зависимости от биологических и экологических свойств древесных пород, возраста дерева, внутренних и внешних условий роста и развития дерева, форма ствола подвержена изменениям.
Научные исследования в области лесной таксации выдвинули ряд методов и гипотез, из которых необходимо отметить следующие (В. К. Захаров (1961, 1967); Н. П. Анучин, (1982):
а) приравнивание формы древесных стволов и частей их к форме правильных стереометрических тел вращения, полных и усеченных;
б) использование законов механики и физики для объяснения формы древесного ствола;
в) непосредственные исследования вида «образующей» древесного ствола с установлением математических уравнений и моделей в виде сплайфункций;
г) характеризовать форму древесного ствола отношениями диаметра на относительных высотах (¼ Н; ½ Н, ¾ Н) и при основании дерева к диаметру на высоте 1,3 м, названных коэффициентами формы gn (предложение А. Шиффеля).
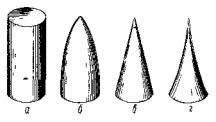
Симметричное строение древесного ствола на вертикальных и поперечных разрезах логически приводит к возможности приравнивания их к форме правильных стереометрических – полных и усеченных тел вращения (рис. 30). Если не учитывать корневых наплывов древесного ствола, то его форму с некоторым допущением можно приравнять к форме параболоида 2- го порядка или же к форме кубического параболоида; вершину древесного ствола с тем же допущением можно рассматривать как конус; комлевую часть с корневыми наплывами – как усеченный нейлоид; наконец, большая средняя часть ствола по форме значительно приближается к форме усеченного параболоида, а на отдельных коротких секциях близка к форме цилиндра.
Рис. 36. Формы правильных тел вращения:
а) цилиндр; б) параболоид; в) конус; г) нейлоид
Эти положения хотя и широко используются в теории и практике лесной таксации, но тем не менее не разрешают проблемы формирования древесного ствола и ни в коем случае, не в состоянии отразить индивидуальные особенности формы отдельных древесных стволов.
Использование законов механики и физики для объяснения формы древесного ствола нашло отражение в исследованиях Метцгера, П. Д. Козицына, Гогенадля и др.
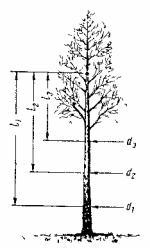
Рис. 37. Зависимость диаметров стволов от расстояния до точки приложения изгибающей силы ветра
По гипотезе Метцгера (1898) и П. Д. Козицына (1909) формирование древесного ствола происходит согласно законам строительной механики, и дерево должно противостоять опрокидывающей силе ветра, направленной на точку приложения силы в центре кроны. Отсюда, по заключению Метцгера, кубы диаметров стволов, замеренных на различном расстоянии от точки приложения силы, должны быть пропорциональны расстоянию до точки приложения опрокидывающей силы (рис. 37):
d13 : d23 : d33 : : dn3 = l1 : l2 : l3 : : ln
П. Д. Козицын находя предложение Метцгера применимым лишь для безъядерных древесных стволов, уточнил показатели степени диаметров для ядровых пород, заменив третью степень степенью 4,5, т. е. принял следующие соотношения:
d14,5 : d24,5 : d34,5 : : dn3 = l1 : l2 : l3 : : ln
Сопоставление данных, полученных по приведенным соотношениям, с фактическим обмером показало, что во многих случаях получаются совпадения размеров, но полного согласования не бывает.
Гогенадль в отличие от Метцгера и П. Д. Козицына высказал предположение, что главным фактором, обусловливающим форму стволов, является их собственный вес и вес кроны, а не изгибающая сила ветра, т. е. ствол должен быть телом равного сопротивления раздавливанию своим весом. На основе такого заключения Гогенадль пришел к выводу, что образующая дре-
весного ствола должна быть логарифмической кривой и выражена в общем виде равенствам:
d 2 = Ae f (x) ,
где А – постоянный коэффициент, различный для отдельных пород; е
– основание Неперовых логарифмов (2,71828); f(x) – функция расстояния от вершины ствола до искомого диаметра.
Так как кривая древесного ствола имеет два перегиба (в верхней и особенно в нижней части), то поэтому она не укладывается в логарифмическую кривую и лишь в средней части напоминает ее.
Жаккард, Гуттенберг и другие исследователи утверждали, что живой организм – дерево, нельзя приравнивать к простому брусу, находящемуся под влиянием сил только внешнего воздействия, что на формирование древесного ствола, помимо механических факторов, оказывают влияние анатомическое строение, физиологические процессы и т. д.
В рассматриваемых гипотезах на первый план выдвигаются лишь отдельные факторы и в комплексе они не рассматриваются, что делает эти гипотезы односторонними, и они не могут быть научной основой для общих способов определения объемов стволов.
Иное направление имеют исследования Д. И. Менделеева, И. Г. Белоновского , Хойера и других; они поставили перед собой задачу установить вид «образующей» древесного ствола и выразить ее соответствующими математическими уравнениями, не исследуя факторы, под влиянием которых происходит формирование древесного ствола.
При этом они исходили из общей зависимости между диаметром ствола d и его высотой Н, выражаемой уравнением общего вида:
у= f(x).
Д.И. Менделеев (1899) и И. Г. Беленовский (1917) предложили использовать для характеристики «образующей» древесных стволов наиболее простую форму этой функции в виде уравнения второго порядка и кубической пара-
болы.
Y = А + Вх + Сх2,
Y = А + Вх + Cx2 + Dx3,
где А, В, С, D – некоторые коэффициенты; х – расстояние от шейки корня до рассматриваемого сечения. Но уравнение второго порядка не дало удовлетворительных результатов, так как образующая ствола имеет S-образный характер. Лучшие результаты были получены при использовании уравнения третьей степени.
В частности, Д. И. Менделеев использовал параболу третьей степени для определения объемов древесных стволов при изучении лесосырьевой базы металлургической промышленности Урала (1899).
К. Вимменауэр (1918), учитывая влияние корневых наплывов и конусовидной вершины на форму образующей ствола, использовал уравнение четвертой степени:
Y = А + Вх + Сх2 + Dх3 + Ех4
где А, В, С, D, E – коэффициенты, имеющие особую величину для каждого ствола, получаемые путем решения нескольких (n) уравнений с n неизвестными.
Ряд авторов (Хойер, Гогенадль и др.) предложили выражать вид образующей древесного ствола при помощи уравнения логарифмической кривой.
В качестве общей формулы для характеристики формы древесного ствола шведский исследователь Хойер предложил следующее соотношение между D и H:
d= C lgæ c + x ö ,
ç÷
D è c ø
где D – диаметр ствола на высоте 1,3 м, d – диаметр ствола на расстоянии х от вершины, выраженный в процентах от всей высоты ствола Н, С и с – некоторые коэффициенты в зависимости от формы ствола, выраженной через коэффициент формы:
d 1
q2 = d 2 .
1,3
Для стволов осины соотношение Хойера примет вид:
d= 2,21gæ 49,6 + x ö
ç÷
D è 49,6 ø
|
|
|
d0 |
|
d 1 |
|
|
|
d 1 |
|
|
|
d 3 |
|
q |
0 |
= |
; q = |
4 |
; q |
2 |
= |
2 |
; q |
3 |
= |
4 |
, |
|
|
|
1 |
d1,3 |
|
|
d1,3 |
|
|
d1,3 |
|
||||
|
|
|
d1,3 |
|
|
|
|
|
|
|
||||
где d0; d1; d2, d3 – диаметры соответственно при основании ствола, на ¼ высоты, ½ высоты и ¾ высоты.
Таким образом, он обратил внимание на изучение сбега ствола по относительным высотам, что позволило уяснить индивидуальную форму древесных стволов и степень ее изменения в зависимости от отдельных факторов.
Основной недостаток предложения А. Шиффеля заключет в том, что коэффициенты формы хотя и дают, общее представление о форме древесных стволов, но, находясь в зависимости от высоты стволов, искажают представление о действительной их форме. Например, для Н = 2,6 м, q2 = l, а для
стволов c высотой меньше 2,6 м q2 получается больше единицы.
Из сделанного обзора методов изучения формы древесных стволов можно видеть, что эта проблема не получила до сего времени окончательного разрешения и требует дальнейших исследований.
Чтобы исключить влияние высоты дерева и его диаметра на высоте 1,3 м на характеристику формы стволов, В. К. Захаровым была разработана оригинальная методика, заключающаяся в следующем: древесный ствол делится на десять одинаковых по длине секций, равных 0,1 Н; измеряется диаметр ствола в коре и без коры, начиная от шейки корня, а затем в конце каж-