Лабораторная работа № 1 Эмпирические зависимости. Метод наименьших квадратов.

1. Теоретические сведения

При исследовании многочисленных физических, химических, технологических и других процессов очень часто сталкиваются со следующей задачей: в итоге опыта получен ряд значений переменных и, требуется по полученным данным найти аналитическое выражение зависимости междуи. Такая зависимость называетсяэмпирической.

Пусть заданы результаты наблюдений

					…
					…

(1)

и нужно получить такую эмпирическую зависимость

, (2)

где ─ параметры, чтобы значенияв точках, мало отличались от опытных данных

Задача определения эмпирической зависимости состоит из двух этапов:

1. определение вида функциональной зависимости (выбор класса функций, которому должна принадлежать искомая функция ;

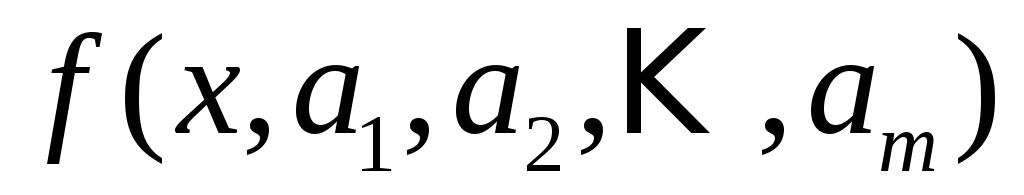2. определение параметров эмпирической зависимости. Определение вида зависимости может быть произведено на основе теоретических представлений о характере изучаемой зависимости или из геометрических соображений. На плоскости 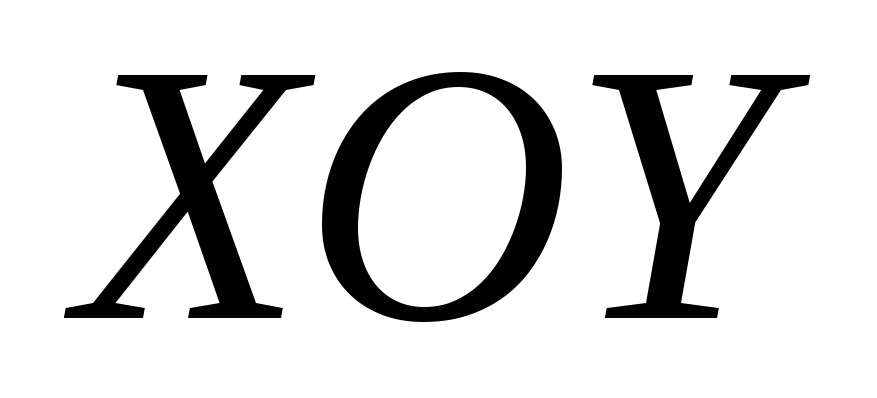строят точки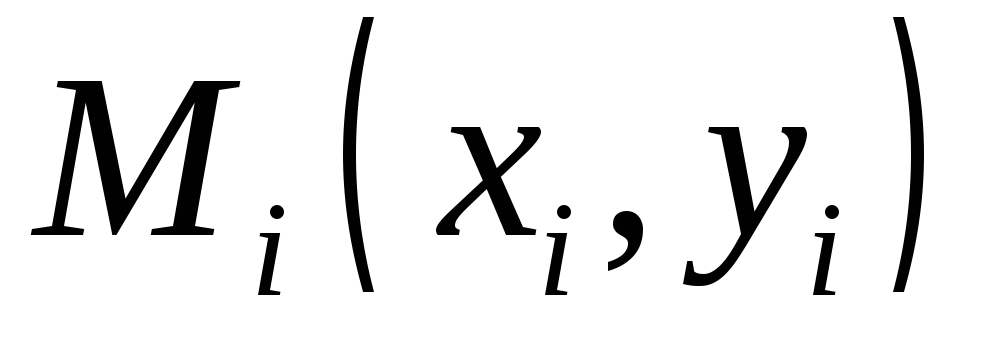,и по характеру их расположения выбирают вид функциональной зависимости. Например, расположение экспериментальных точек может навести на мысль о линейной, или квадратичной, или экспоненциальной или другой зависимости. Однако общего метода для нахождения наилучшего типа эмпирической зависимости, соответствующей опытным данным, указать нельзя.

После того как определен класс, которому должна принадлежать искомая эмпирическая зависимость, встает вопрос о нахождения конкретных значений параметров .

Одним из основных методов нахождения параметров эмпирической зависимости является метод наименьших квадратов. Этот метод не решает вопроса о выборе общего вида аналитической функции, а дает возможность при заданном типе аналитической функции подобрать наиболее вероятные значения для ее параметров.

Сущность метода наименьших квадратов состоит в том, что параметры выбираются из условия минимума суммы квадратов уклонений

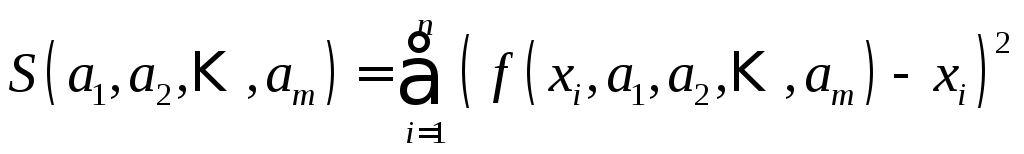(3)

Если рассматривать как непрерывную функцию её параметров, то в точке минимума её частные производные должны равняться нулю, т.е. искомые значения параметров должны удовлетворять системе уравнений

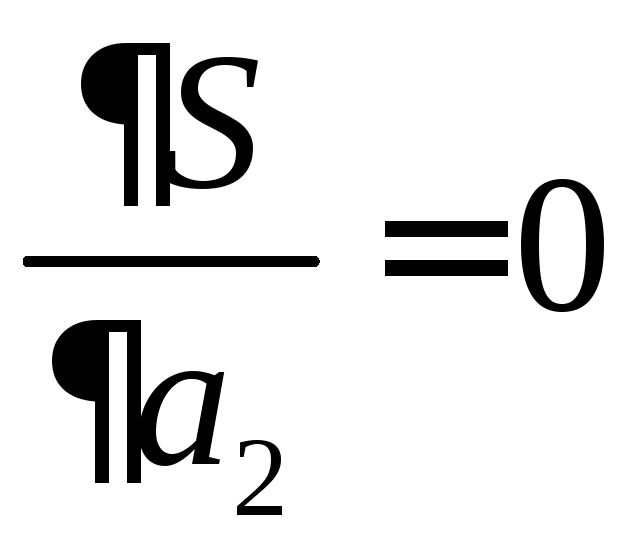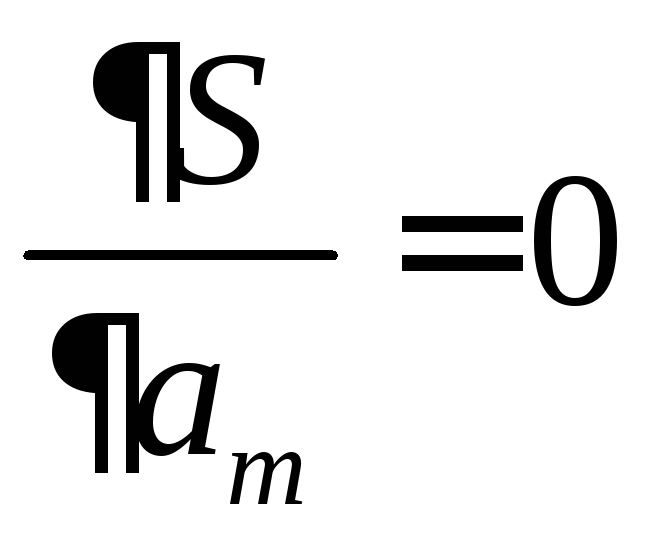, , … ,(4)

Известно, что если в качестве функции берется многочлен, то функцияимеет одну точку экстремума, в которой достигается минимум. Следовательно, в этом случае искомые значенияпредставляют собой решение системы (4). В этом случае

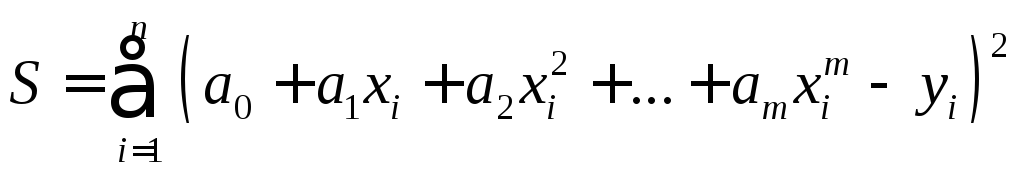
а систему (4) можно преобразовать к виду

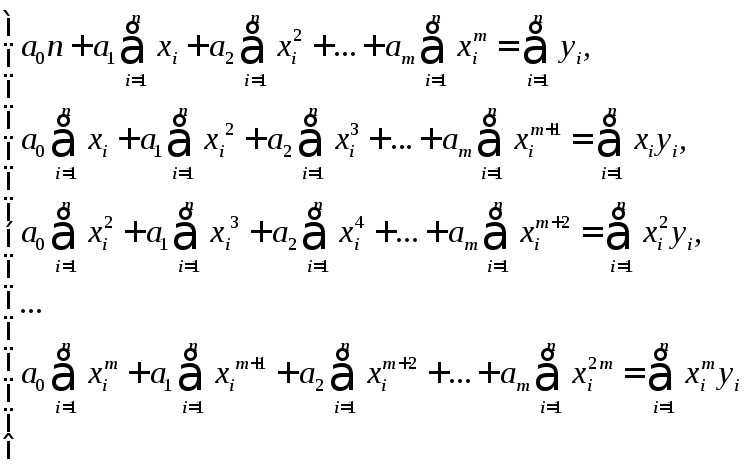(5)

Полученная система решается любым известным методом (Гаусса, Крамера, матричным) или с помощью стандартных программ на компьютере.

Отметим два частных случая наиболее часто встречающихся на практике — случаи линейной и квадратичной зависимости от. Еслизависит отлинейно, то система (5) примет вид

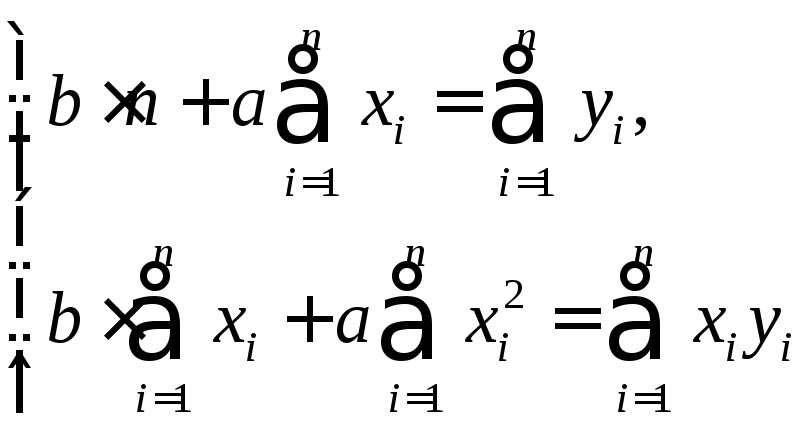(6)

Чтобы получить систему (6), нужно в системе (5) положить .

В случае квадратичной зависимости система (5) преобразуется к виду

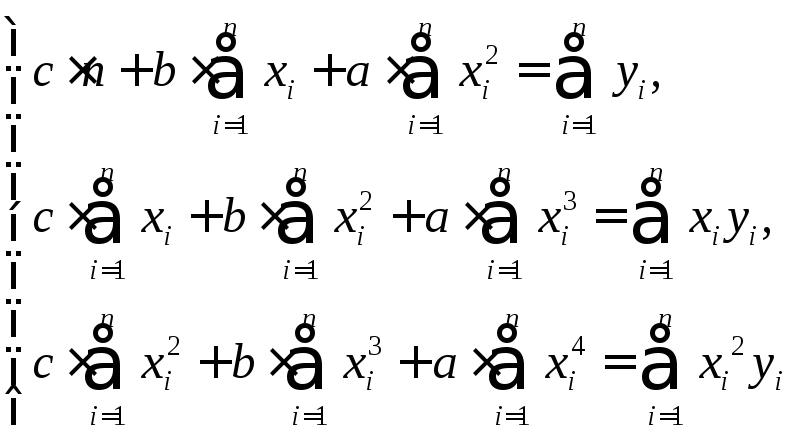(7)

Для этого в системе (5) нужно положить .

Метод наименьших квадратов обладает тем преимуществом, что если сумма квадратов уклонений мала, то сами эти уклонения также малы по абсолютной величине. Кроме того, этот метод допускает веское обоснование с вероятностной точки зрения. Недостатком метода наименьших квадратов является громоздкость вычислений. Поэтому к нему прибегают обычно при обработке наблюдений высокой точности, когда нужно получить также весьма точные значения параметров. Заметим, что в этом случае промежуточные вычисления нужно проводить с достаточным количеством десятичных знаков, так как в противном случае искомые коэффициенты могут иметь мало верных знаков.

2. Примеры решения задач.

Задание 1. Найти эмпирическую зависимость времени валки дерева от его диаметра, по результатам испытаний, приведенных в таблице

d, cм	24	26	28	30	32	34	36	38	40	42
t, c	49	53	54	56	61	62	65	69	72	76

Решение.

Обозначим и. На плоскостипостроим точки,

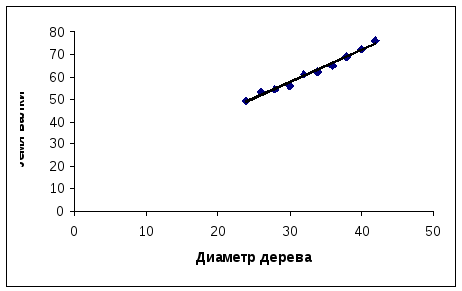
Рис. 1. Точечная диаграмма

Из точечной диаграммы (рис.1) видно, что точки расположены в близи некоторой прямой, поэтому можно считать, что зависимостьотбудет линейной, т.е. имеет вид. Для вычисления коэффициентов системы (6) составим таблицу:

Таблица 1

	xi	yi	xi2	xiyi
1	24	49	576	1176
2	26	53	676	1378
3	28	54	784	1512
4	30	56	900	1680
5	32	61	1024	1952
6	34	62	1156	2108
7	36	65	1296	2340
8	38	69	1444	2622
9	40	72	1600	2880
10	42	76	1764	3192
∑	330	617	11220	20840

Система (6) для нашего примера имеет вид:

Из нее находим коэффициенты и:,.

Искомая эмпирическая функция будет . На рис.1 построим график полученной прямой. Точечная диаграмма и график эмпирической зависимости подтверждает их соответствие.

Решение при помощи Excel.

Нахождение эмпирических формул методом наименьших квадратов можно осуществлять в среде Excel, используя:

• функции СТЕПЕНЬ, ПРОИЗВЕД, СУММ, СУММКВ, СУММПРОИЗВ,

• формулы массива МОБР, МУМНОЖ,

• графический анализ с помощью Линий тренда.

Рассмотрим на конкретных примерах, как работают эти функции.

1. Внесите данные задачи в ячейки B4:B13 и C4:C13.

2. Вычислите , введя в ячейкуD4 формулу

=B4*B4

и затем скопировав ее в ячейки D5:D13 (направив указатель мыши на черный квадрат в правом нижнем углу ячейки, чтобы он принял вид черного крестика, и протащив в ячейку D5 и т.д.).

Аналогично найдите произведения и результат запишите в ячейкахE4:E13.

Эти же результаты можно получить, используя функции СТЕПЕНЬ и ПРОИЗВЕД в категории Математические Мастера функций.

3. Найдите сумму значений в ячейках B4:B13 и результат запишите в ячейку B14. Для этого выделим соответствующие ячейки и нажмем пиктограмму суммирование на Панели инструментов. Для суммирования элементов массива можно воспользоваться функциями СУММ, СУММКВ, СУММПРОИЗВ в категории Математические Мастера функций.

3. Система (6) для нашего примера имеет вид:

Обозначим − матрица системы,− столбец свободных членов,− столбец неизвестных. Систему решите матричным методом по формуле:, выполнив действия, записанные ниже.

• В ячейках L3:M4 запишите матрицу А.

• Найдите обратную матрицу 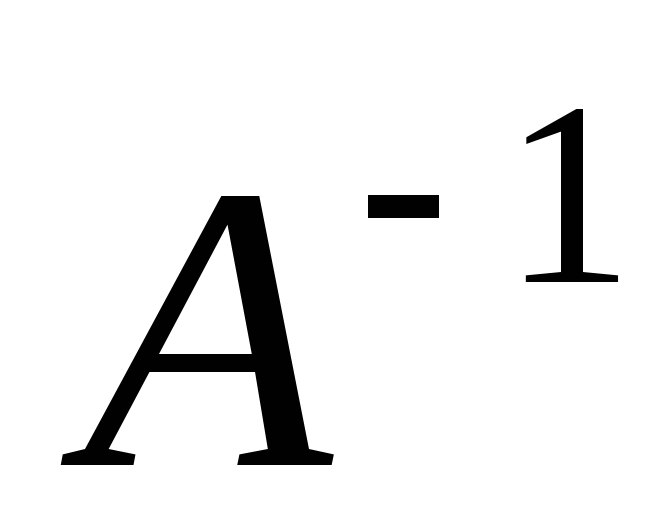. Для этого выделите область соответствующего размера диапазонL6:M7 для записи обратной матрицы. Вызовите формулу массива

→Математические → МОБР → ОК.

Задайте адреса матрицы А L3:M4 и нажмите Ctrl+Shift+Enter для выполнения действия.

• В ячейках M9:M10 запишите столбец свободных членов B.

• Умножьте матрицу 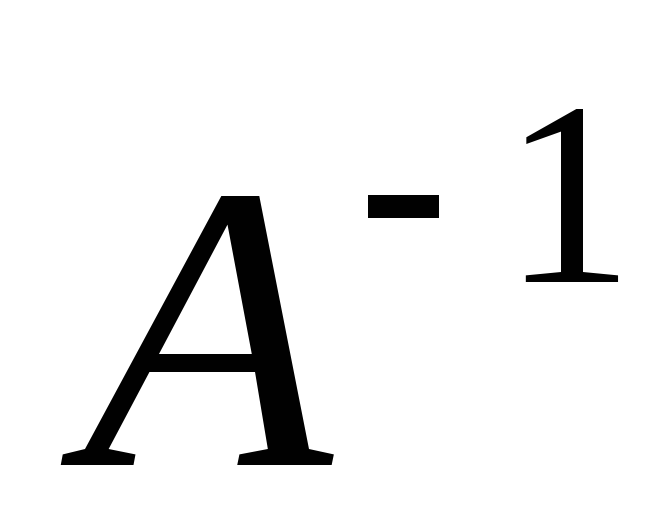на В и результат запишите в ячейкахM12:M13. Для этого выделите диапазон ячеек M12:M13. Вызовите формулу массива

→Математические → МУМНОЖ → ОК.

Задайте адреса перемножаемых матриц L6:M7 и M9:M10 и нажмите Ctrl+Shift+Enter для выполнения действия.

Таким образом, искомая эмпирическая функция имеет вид .

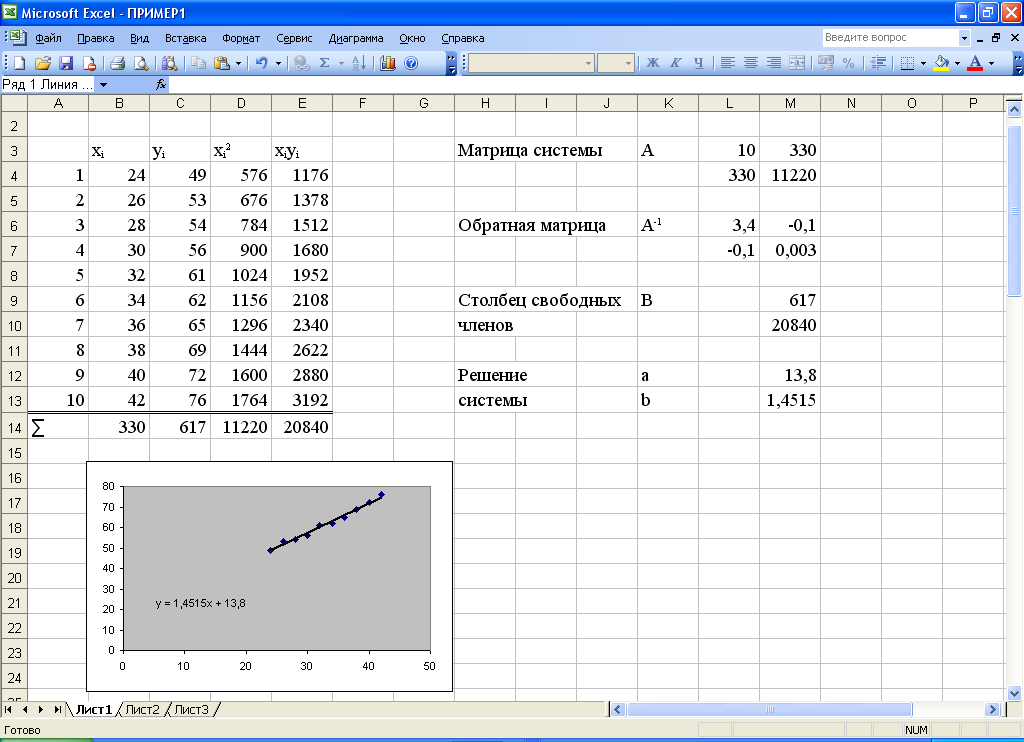
Рис.2. Рабочий лист 1

4. Постройте точечную диаграмму зависимости t от d. используя Мастер диаграмм, который вызывается с помощью команды Вставка → Диаграмма или при нажатии соответствующей кнопки на панели инструментов.

• Выделите данные, которые будут включены в диаграмму, т.е. ячейки B4:C13.

• Выберите команду Вставка → Диаграмма (можно щелкнуть кнопку Мастер диаграмм на панели инструментов).

• На первом шаге работы Мастера диаграмм выберите Тип диаграммы вариант Точечная и щелкните Далее. Можно пропустить остальные шаги и сразу нажать кнопку Готово. На экране появится встроенный график. При необходимости его можно перетащить в более удобное место, зацепив мышью за край области диаграммы.

• Добавьте к исходной точечной диаграмме линию тренда. Для этого используйте команду меню Диаграмма → Добавить линию тренда, которая появляется, если диаграмма выделена.

• В окне Линия тренда во вкладке Тип и выберите шаблон кривой. В нашем случае Линейная . Во вкладкеПараметры поставьте флажок: Показывать уравнение на диаграмме и нажимите ОК.

На диаграмме появится линия тренда и ее уравнение (рис 2).

Задание 2. Установить вид эмпирической зависимости y от x и методом наименьших квадратов найти ее параметры для следующих значений и:

	0,78	1,56	2,34	3,12	3,81
	2,50	1,20	1,12	2,25	4,28

Решение. На плоскости построим точки,.

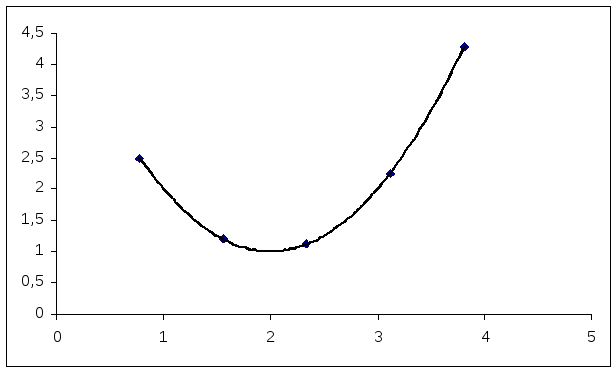
Рис. 3. Точечная диаграмма

Из точечной диаграммы (рис.3) видно, что точки расположены в близи некоторой параболы, поэтому можно считать, что зависимостьотбудет квадратичной, т.е. имеет вид. Для вычисления коэффициентов системы (7) составим таблицу:

0,78 0,6084 0,4746 0,3702 2,50 1,9500 1,5210 1,56 2,4336 3,7964 5,9224 1,20 1,8720 2,9203 2,34 5,4756 12,8129 29,9822 1,12 2,6208 6,1327 3,12 9,7344 30,3713 94,7585 2,25 7,0200 21,9024 3,81 14,5161 55,3063 210,7172 4,28 16,3068 62,1289

11,61 32,7681 102,7615 341,7505 11,35 29,7696 94,6053

Система (7) для нашего примера имеет вид:

Решая её, например, по формулам Крамера, находим, что ,,. Следовательно, зависимостьотимеет вид:

.

Решение при помощи Excel. Все исходные, промежуточные данные и результаты решения изображены на рабочем листе2 (рис.4).

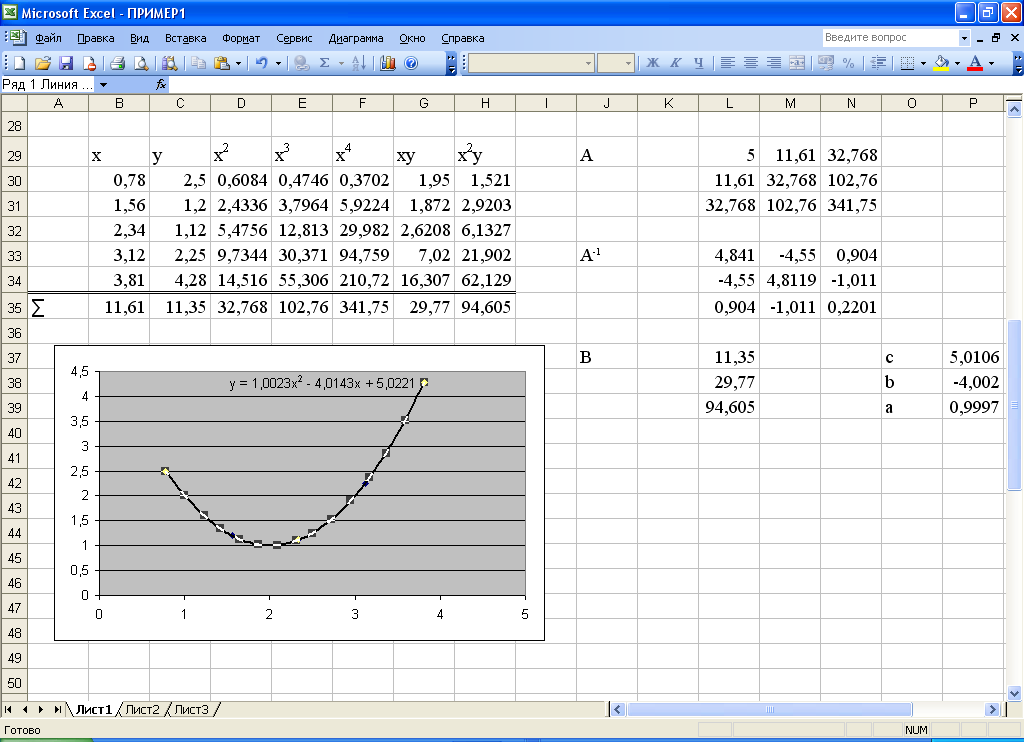
Рис.4. Рабочий лист 2

Система (6) для нашего примера принимает вид:

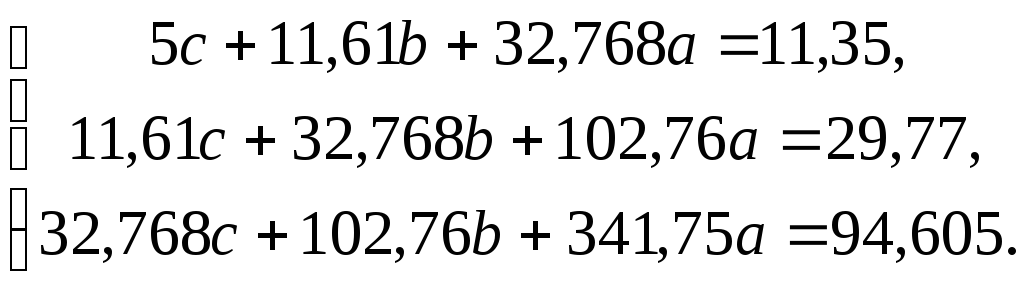
Следовательно, зависимость отимеет вид:

.