Решение

Пусть на множестве задано бинарное отношение эквивалентности. По определению эквивалентности оно должно быть рефлексивным, симметричным и транзитивным. Бинарное отношение на называется рефлексивным, если , пара принадлежит отношению . Это значит, что соответствующий граф имеет в каждой вершине петлю.

Бинарное отношение называется симметричным, если из того, что следует, что . Это значит, что граф симметричного отношения должен быть симметричным (т.е. пара дуг и – составляет ребро графа, соединяющее вершины и (или и )).

Бинарное отношение называется транзитивным, если из того, что и следует, что . Значит, если в соответствующем графе есть ребра, соединяющие вершины и , и , то обязательно есть ребро, соединяющее и .

Известно, что задание на множестве бинарного отношения эквивалентности равносильно разбиению множества на попарно непересекающиеся классы, так что в один класс попадают все элементы, эквивалентные между собой.

Таким образом, граф отношения эквивалентности распадается на компоненты связности. Каждая компонента связности соответствует одному из классов; при этом все вершины каждой компоненты попарно соединены ребрами, и каждая вершина имеет петлю. Например, граф

Задает отношение эквивалентности на множестве:

,

которое разбивает это множество на классы: , , .

Бинарное отношение задает отношение частичного порядка (не строгого), если оно рефлексивно, антисимметрично и транзитивно. Отношение называется антисимметричным, если из того, что граф антисимметричного отношения из двух дуг , следует, что . Это значит, что граф антисимметричного отношения из двух дуг и содержит не более одной. Другими словами, если и граф содержит, например, дугу , то он не содержит дуги .

Значит, граф антисимметричного отношения ориентирован, он содержит только дуги, но не ребра.

Н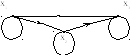 апример, задает линейный порядок на множестве . Граф этого отношения

И ногда граф частичного порядка упрощают. Опускают петли и считают, что , если существует ориентированный путь из в . Тогда граф того же отношения можно изобразить так

Элемент частного упорядоченного множества является минимальным, если не существует дуги, исходящей из . Элемент называется максимальным, если не существует дуги, заходящей в .

Элемент называется наименьшим, если для всякой вершины существует дуга, исходящая из и заходящая в .

Наименьший элемент является минимальным, но минимальный может и не быть наименьшим. Минимальных элементов может быть несколько, наименьших один. Например у графа

Минимальных элементов – два, максимальных – два, наименьшего или наибольшего – нет.

У графа

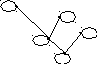
Наибольших элементов – нет, максимальных – три, наименьший – один, он же минимальный.

Задачи для самостоятельного решения.

1. Доказать, что ребро графа тогда и только тогда является перешейком, когда не существует цикла, содержащего данное ребро.

2. Доказать, что на любом связном графе с вершинами нечетной степени имеется семейство из цепей, которые в совокупности содержат все ребра графа по одному разу.

Указание: добавить ребер, соединяющих вершины нечетной степени так, чтобы в полученном графе степени всех вершин были четны и к полученному графу применить теорему Эйлера.

3. Доказать, что в полном ориентированном графе всегда найдется ориентированная элементарная цепь, проходящая через все его вершины (граф называется полным, если любые две его вершины соединены другой).

4. Чему равно число ребер полного графа с вершинами? Ответ: .

5. Д оказать, что графы, изображенные на рис.3 попарно не изоморфны между собой.

6. Д оказать, что графы, изображенные на рис.4 не изоморфны.

7. Построить граф по матрице смежности.

(а) (б) (в)