Плоские графы. Эйлерова характеристика плоскости. Некоторые алгоритмические задачи теории графов

Теоретические вопросы

1. Определение плоской реализации графа.

2. Какой граф называется плоским?

3. Что называется наложением одной плоской реализации графа на другую?

4. Определение эйлеровой характеристики плоского связного графа.

5. Теорема Эйлера.

6. Определение связного графа.

7. Почему эйлерову характеристику плоского связного графа называют эйлеровой характеристикой плоскости?

8. Какие графы не являются плоскими? Почему? Приведите примеры графов, не имеющих плоской реализации.

9. Сформулировать теорему Понтрягина-Куратовского.

10. Существуют ли поверхности, эйлерова характеристика которых отлична от эйлеровой характеристики плоскости?

Решение задач

№1. Показать, что данный граф является плоским:

Решение

Изобразим тот же граф следующим образом:

Действительно, каждый из этих графов может быть задан одним и тем же множеством вершин и ребер: , .

№2. Показать, что данный граф не является плоским.

Р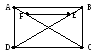ешение

Покажем, что этот граф изоморфен графу, который, как известно, не является плоским. Действительно, группы вершин и

в каждом из этих графов не соединены ребрами внутри группы и каждая из вершин одной группы соединена ребрами с каждой вершиной другой группы.

Одновременно мы видим, что если в данном графе удалить одно из ребер, например, , то полученный граф будет плоским.

Замечание. Числовая характеристика, одинаковая для всех изоморфных графов, называется инвариантом графа. Инвариантами графа являются, например, количество вершин и ребер, степени вершин, количество ребер в циклах и т.д. Не известно никакого набора инвариантов, определяющих граф с точностью до изоморфизма.

№3. Найти все графы с шестью вершинами, не являющиеся плоскими.

Решение

Используя теорему Понтрягина-Куратовского можно сделать вывод, что всякий такой граф либо изоморфен графу с шестью вершинами предыдущей задачи, либо получается из него добавлением ребер.

Либо это может быть полный граф с пятью вершинами с добавленной к нему изолированной вершиной и все графы, которые можно получить из него добавлением ребер. Например

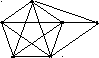
№4. Проверить формулу Эйлера для графа квадратной мозаики, составленного из квадратов.

Решение

Число вершин – . Подсчитаем число ребер. На каждой вертикальной полосе имеем ребер, вертикальных полос – , таким образом всего на мозаике имеем вертикальных ребер и столько же горизонтальных, значит .

Число плоских областей (число малых квадратов и бесконечная область плоскости). Поэтому .

№5. Доказать, что эйлерова характеристика связного плоского графа равна двум индукцией по числу ребер графа.

Решение

Возьмем граф с одной изолированной вершиной , тогда , , , . Итак, для связного графа с числом ребер нуль утверждение верно.

Пусть утверждение уже доказано для всех связных плоских графов с ребрами. Добавим еще одно ребро. Если добавляемое ребро соединяет уже существующие вершины, то

, , и .

Если добавляемое ребро соединяет существующую вершину с новой, то , , и .

Утверждение доказано.

№6. Доказать, что для связного плоского графа при имеет место соотношение .

Доказательство

Каждая грань ограничена, по крайней мере, тремя ребрами, каждое ребро ограничивает не более двух граней, отсюда , имеем , отсюда

или .

Замечание. Доказанное соотношение является необходимым условием для связного плоского графа. Это условие не является достаточным. Например, для полного графа с пятью вершинами, не являющимся плоским, имеем , , откуда , т.е. этот граф не может быть плоским.

Однако для графа с шестью вершинами, не являющегося плоским имеем , , откуда ,. Этот результат получается потому, что существует плоский граф с шестью вершинами и девятью ребрами. Граф с шестью вершинами, который не имеет плоской реализации имеет длину любого цикла не менее четырех ребер, поэтому для этого графа имеем оценку числа ребер: , что приводит к тривиальному неравенству.

Эйлер вывел свою формулу, исследуя выпуклые многогранники. Действительно, развертка многогранника – это плоский граф. Эти вопросы – пример чисто математических вопросов в теории графов.

В теории графов имеется большое количество алгоритмических задач. С некоторыми из них мы уже встречались. Например, задача о построении эйлерова цикла. Известно, что если степени всех вершин графа четны, то существует эйлеров цикл.

Как построить его? Оказывается, достаточно выполнить следующие условия.

Алгоритм построения эйлерова цикла.

1. Выбрать произвольно некоторую вершину .

2. Выбрать произвольно некоторое ребро , инцидентное , и присвоить ему номер 1 (назовем это ребро пройденным).

3. Каждое пройденное ребро вычеркивать и присваивать ему номер, на единицу больший номера предыдущего вычеркнутого ребра.

4. Находясь в вершине , не выбирать ребра, соединяющие 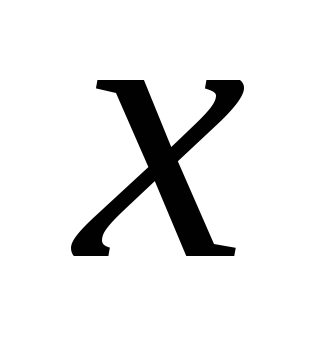с , если только есть возможность выбора.

5. Находясь в вершине , не выбирать ребра, которые являются "перешейком" (при удалении которого граф, образованный не зачеркнутыми ребрами, распадается на две компоненты связности, имеющие хотя бы по одному ребру).

6. После того, как в графе будут занумерованы все ребра, цикл, образованный занумерованными ребрами будет эйлеровым.

Обоснование этого алгоритма несложно. Невозможность выполнить предписание алгоритма может возникнуть только в вершине , если попасть в нее, по крайней мере, во второй раз. В отличие от других вершин, степень этой вершины остается четной при попадании в нее в -й раз . Если эта степень равна нулю, алгоритм перестает работать. В этом случае по правилу 3 любое ребро может войти не более одного раза, в силу правил 4 и 5 – пройдены все ребра.

№7. Найти эйлеровы циклы в графах: