Основные понятия и определения теории графов. Теорема Эйлера (о существовании эйлеровых циклов)

Теоретические вопросы

1. Дать определение графа, вершин, дуг.

2. Приведите примеры графа.

3. Дать определение петли и ребра.

4. Определение симметрического графа.

5. Определение пути и контура, цепи и цикла.

6. Простые и элементарные пути и цели.

7. Дать определение суграфа, подграфа и части графа.

8. Дать определение сильно связного и связного графов, компоненты связности.

9. Определение тупика и перешейка.

10. Полустепени исхода и захода. Степень вершины, степень вершины симметрического графа.

11. Определение матрицы смежности графа. Почему матрица смежности симметрического графа будет симметрической (т.е. )?

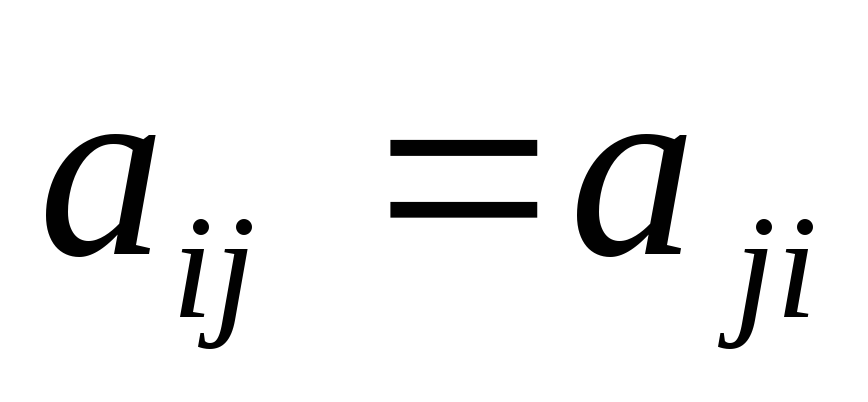12. Определение изоморфизма графов.

13. Задача о кенигсбергских мостах.

14. Теорема Эйлера (о существовании эйлеровых циклов в симметрическом связном графе).

15. Задача о четырех красках.

16. Головоломка Гамильтона (о существовании элементарного (гамильтонова) цикла на правильном додекаэдре).

Решение задач

№1. Доказать, что для связного графа число ребер равно полу сумме степеней всех его вершин.

Доказательство

Докажем предложение индукцией по числу ребер связного графа. Связный граф с одним ребром имеет вид (1) или (2).

С умма степеней вершин каждого из этих графов равна 2. Предположим, что доказываемое предложение верно для всех связных графов, содержащих ребро, и рассмотрим граф с ребрами.

Удалим в этом графе произвольное ребро, получим граф с тем же числом вершин и с ребром. По предложению индукции сумма степеней всех вершин полученного графа равна .

Добавим к полученному графу удаленное ребро, тогда сумма степеней всех вершин графа увеличится на 2 (если удаленное ребро – петля, то она увеличивает сумму степеней инцидентной ей вершины на 2, если ребро не является петлей, то оно инцидентно двум вершинам и, значит, увеличивает степень каждой из них на 1). Таким образом, сумма степеней всех вершин связного графа с ребрами равна . Предложение доказано.

№2. Доказать, что для того, чтобы на связном графе имелась цепь , содержащая все его ребра по одному разу, необходимо и достаточно, чтобы вершины и были единственными вершинами нечетной степени графа.

Доказательство

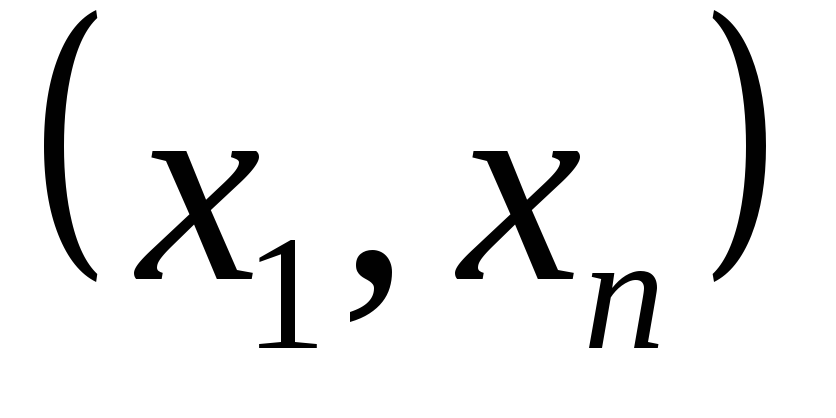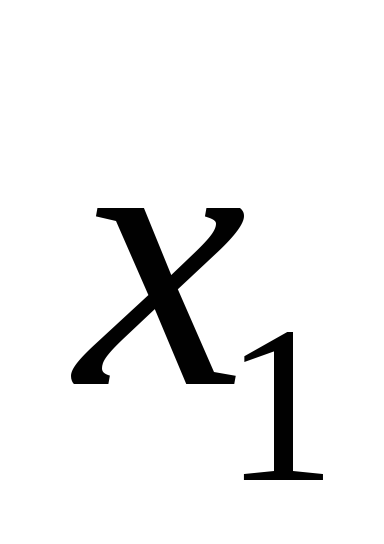1. Пусть – цепь, содержащая все ребра графа по одному разу. Добавим к данному графу ребро . Тогда получим эйлеров цикл (т.к. он содержит все ребра полученного графа по одному разу). Но по теореме Эйлера на связном графе существует эйлеров цикл тогда и только тогда, когда степени все его вершин четны. Таким образом, в частности, степени вершин и – четны. 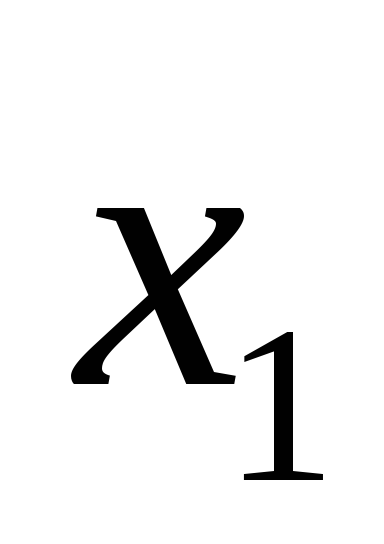Удалим теперь из полученного графа добавленное ребро , получим исходный граф, в котором степени вершин и 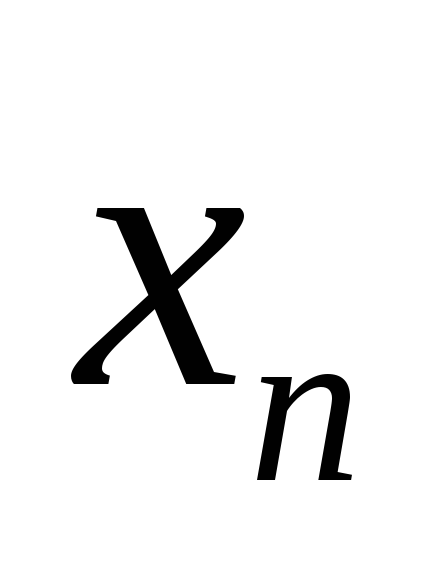будут нечетны, а степени остальных вершин – четны.

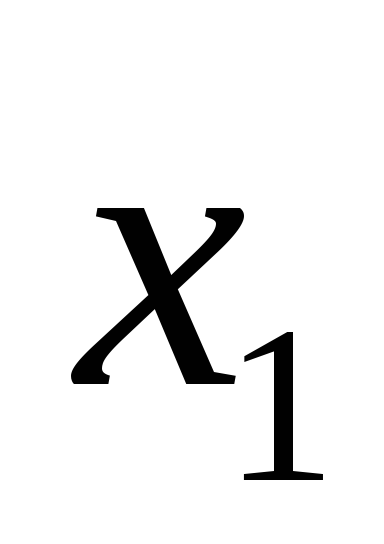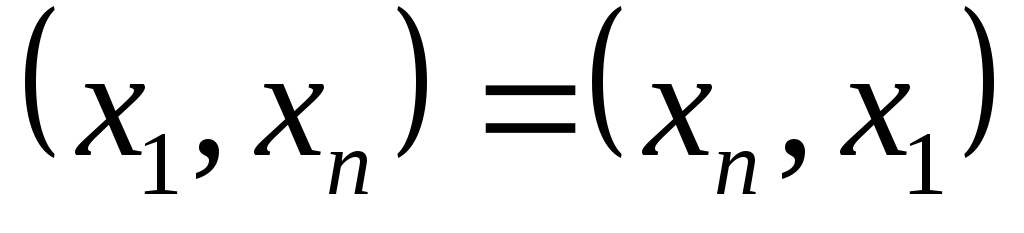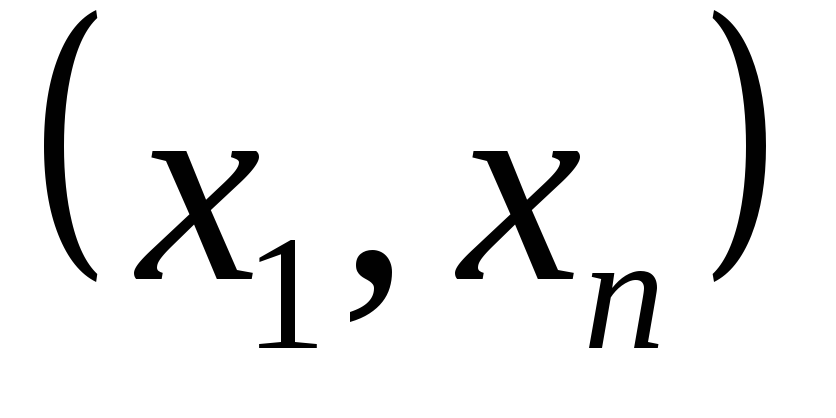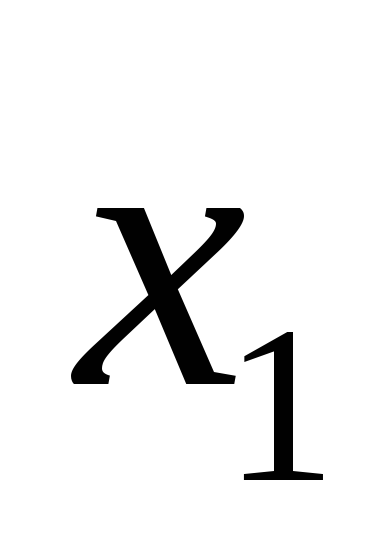2. Пусть теперь дан связный граф, у которого единственные вершины нечетной степени – это и . Рассмотрим граф, полученный из данного добавлением ребра . Тогда в полученном графе степени всех вершин четны; по теореме Эйлера в полученном графе существует эйлеров цикл. Удалим теперь добавленное ранее ребро , получим исходный граф, в котором имеется цепь, соединяющая вершины и 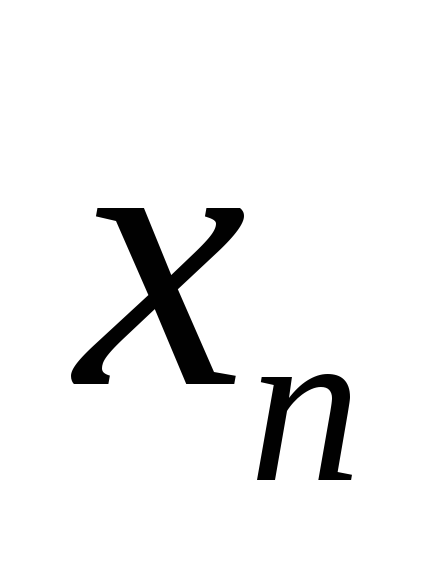. Предложение доказано.

№3. Доказать, что дерево с вершинами имеет ребер.

Доказательство

Докажем предположение индукцией по числу ребер графа. По определению, дерево – связный граф без циклов (в частности, без петель).

Поэтому дерево, содержащее одно ребро, может иметь только две вершины, инцидентные данному ребру. Будем считать, что доказываемое предположение выполнено для всех деревьев, содержащих ребер (такое дерево имеет по предположению индукции вершины). Рассмотрим произвольное дерево с ребрами. Такой граф обязан иметь тупик (т.е. вершину степени ). Удалив тупик вместе с вершиной степени , мы получим граф с ребрами и вершиной. Значит, граф с ребрами имеет на единицу больше ребер и вершин.

Предположение доказано.

Замечание. Можно было бы доказать это предположение индукции по числу вершин. Так как дерево не имеет циклов, то каждое новое ребро добавляет новую вершину (если соединить в дереве любые две старые вершины, то получим цикл).

№4. Доказать, что графы, изображенные на рис.1 изоморфны.

Рис. 1.