§2. Примитивно рекурсивные функции.

Операции над числовыми функции назовем операторами. В этом параграфе мы определим ряд операторов, обладающих тем свойством, что, применяя их к функциям, вычислимым в интуитивном смысле, мы получим функции, также вычислимые в интуитивном смысле.

Частичные функции, которые можно получить при помощи этих операторов из простейших функций , ,, называютсячастично рекурсивными.

Основная гипотеза Черча состоит в том, что класс частично рекурсивных функций совпадает с классом функций, допускающих машинное или алгоритмическое вычисление.

Суперпозиция частичных функций.

Пусть заданы n частичных функций от одного и того же числа m переменных, определенных на множестве Х со значениями во множестве Y, и пусть на множестве Y определена частичная функция f от n переменных со значениями во множестве Z. Введем частичную функцию g от m переменных на множестве X со значениями во множестве Z, полагая по определению, что выполняется равенство: для произвольных переменных .

Говорят, что функция g получается операцией суперпозиции или подстановки из функций . Оператор подстановки будем далее обозначать символом . В качестве множеств X, Y, Z далее всюду будет браться множество натуральных чисел N.

Например, значение терма не определено, а значение терма, где- символы простейших функций, определенных в предыдущем параграфе.

Оператор примитивной рекурсии.

Пусть заданы числовые частичные функции: n-местная g и (n+2)–местная функция h. Тогда (n+1)–местная частичная функция f получается из функций g и h примитивной рекурсией, если для всех натуральных значений имеем следующие соотношения:

,

.

(Напомним, что N = 0, 1, 2, 3, …, поэтому это определение верно и для случая, когда ).

Например, одноместная частичная функция f получена примитивной рекурсией из постоянной одноместной функции, равной числу а и двуместной частичной функции h, если

,

.

Теорема 1: Для любых частичных n–местной функции g и (n+2)–местной функции h (n=0,1,2,…) существует одна и только одна частичная (n+1)–местная функция f, получаемая из g и h примитивной рекурсией.

Доказательство: Действительно, если функция f существует, то по определению последовательно находим:

,

,

……………………………………

,

и поэтому f определена однозначно. Из этих соотношений видно, что если для некоторых значениенеопределенное, то и для всехзначениябудут также неопределенные.

Если функции g и h заданы, то приведенные равенства можно принять за определение функции f. Теорема доказана.

Из доказательства предыдущей теоремы видно, что если мы каким-то образом «умеем» находить значения функций g и h, то значения функции f можно вычислить при помощи процедуры механического характера. Для нахождения значения достаточно последовательно найти числа:

,

,

,

…………………,

.

Полученное на (m+1)-м «шаге» число и будет искомым значением функцииf в точке .

Изложенный процесс вычисления будет продолжаться неограниченно только в том случае, когда неограниченным окажется процесс вычисления одного из выражений , ,…,, т.е. когда хотя бы одно из этих выражений будет иметь неопределенное значение. В этом случае и значениебудет неопределенным.

Определение: Пусть задана система G каких-то частичных функций. Частичная функция f называется примитивно рекурсивной относительно G, если f можно получить из функций системы G и простейших функций конечным числом операций подстановки и примитивной рекурсии.

Функция f называется просто примитивно рекурсивной, если ее можно получить конечным числом операций подстановки и примитивной рекурсии, исходя лишь из простейших функций .

Операции подстановки и примитивной рекурсии, применяемые к всюду определенным функциям, дают в результате снова всюду определенные функции. Поэтому, в частности, все примитивно рекурсивные функции всюду определены.

Из определения также следует, что примитивно рекурсивные функции будут примитивно рекурсивны относительно любой системы функций.

Наконец, из определения также следует, что операции подстановки и примитивной рекурсии, примененные к частичным функциям, примитивно рекурсивным относительно какой-нибудь системы функций G, дают в результате снова функции, примитивно рекурсивные относительно G.

Согласно определению одноместные функции и многоместные функции примитивно рекурсивны.

Для n-местной функции имеем представлениеи поэтому- примитивно рекурсивна.

Произвольная n-местная постоянная функции допускает представление в виде терма , записанного при помощи символов примитивно рекурсивных функций и предметных переменных.

Двуместная функция удовлетворяет соотношениям:

,

.

Следовательно, функция возникает из примитивно рекурсивных функций,операцией примитивной рекурсии и поэтому функцияпримитивно рекурсивна.

Двуместная функция xy удовлетворяет примитивной рекурсии:

,

с начальными примитивно рекурсивными функциями

,

поэтому функция xy примитивно рекурсивна.

Рассмотрим функцию , причем будем считать, что. Соотношения, представляют собой рекурсивную схему с начальными примитивно рекурсивными функциями. Поэтому функциятакже примитивно рекурсивна.

В математическом анализе иногда встречается функция (сигнум или знак числа х), равная (+1) для положительных вещественных чисел х, (-1) - для отрицательных х, и 0 для чисел . Мы рассмотрим эту функцию для натуральных значенийх. По определению:

Введем противоположную функцию:

Эта функция совпадает с разностью . Функциииудовлетворяют примитивным рекурсивным схемам:

Поэтому они примитивно рекурсивны.

В области натуральных чисел разность естественно считать частичной двуместной функцией от переменных, определённой лишь для, т. к. отрицательные числа не входят в рассматриваемую область. Но примитивно рекурсивные функции всюду определённые. Поэтому вместо обычной разности вводят усеченную разность, определяемую следующим образом:

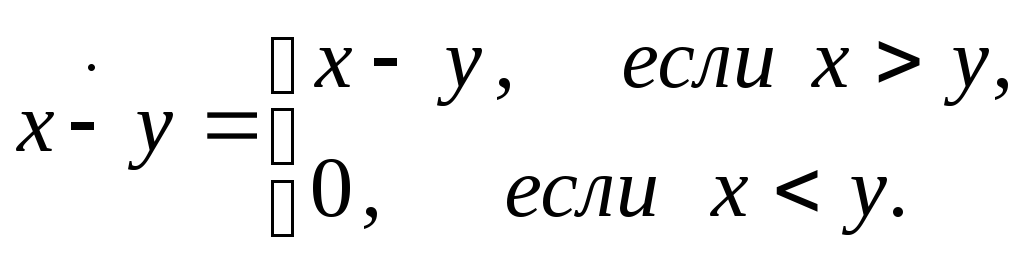
В отличие от обычной разности усеченная разность в области натуральных чисел всюду определена. Функция удовлетворяет примитивно рекурсивной схеме:

с примитивно рекурсивными начальными функциями и. Поэтому функцияпримитивно рекурсивна. С другой стороны, из определения усечённой разности следует, что для любыхимеем:

.

Это означает, что двуместная функция получается примитивной рекурсией из функцийи . Обе последние функции примитивно рекурсивны. Поэтому и функция примитивно рекурсивна.

Наконец из примитивной рекурсивности функций ивытекает примитивная рекурсивность функции. Можно доказать примитивную рекурсивность ряда арифметических и других числовых функций.