Лекция № 5. Множества и подмножества

1. Задание множеств

Если объект является элементом множества, то говорят, чтопринадлежит. Обозначение. В противном случае говорят, чтоне принадлежит. Обозначение.

Множество, не содержащее элементов, называется пустым. Обозначение: .

Чтобы задать множество, нужно указать, какие элементы ему принадлежат. Это можно сделать различными способами.

• Перечислением элементов: .

• Характеристическим предикатом: .

• Порождающей процедурой: .

При задании множеств перечислением обозначения элементов обычно заключают в фигурные скобки и разделяют запятыми. Характеристический предикат (от латинского praedicatum) – это некоторое условие, выраженное в форме логического утверждения, возвращающего логическое значение. Если для данного элемента условие выполнено, то он принадлежит определяемому множеству, в противном случае – не принадлежит. Порождающая процедура – это процедура, которая, будучи запущенной, порождает некоторые объекты, являющиеся элементами определяемого множества.

Пример 5.1. ;

;

.

2. Парадокс Рассела

Задание множеств характеристическим предикатом может приводить к противоречиям. Например, все рассмотренные в примерах множества не содержат себя в качестве элемента. Рассмотрим множество всех множеств, не содержащих себя в качестве элемента: .

Если множество существует, то мы должны иметь возможность ответить на следующий вопрос:? Пусть, тогда. Пусть, тогда. Получается неустранимое логическое противоречие, которое известно какпарадокс Рассела. Существует три способа избежать этого парадокса.

1. Ограничить используемые характеристические предикаты видом

где – известное, заведомо существующее множество (универсум). Обычно при этом используют обозначение. Дляуниверсум не указан, а потомумножеством не является.

2. Теория типов. Объекты имеют тип 0, множества имеют тип 1, множества множеств – тип 2 и т.д. не имеет типа и множеством не является.

3. Характеристический предикат задан в виде вычислимой функции (алгоритма). Способ вычисления значения предикатане задан, а потомумножеством не является.

Последний из перечисленных способов лежит в основе так называемого конструктивизма – направления в математике, в рамках которого рассматриваются только такие объекты, для которых известны процедуры (алгоритмы) их порождения. В конструктивной математике исключаются из рассмотрения некоторые понятия и методы классической математики, чреватые возможными парадоксами.

3. Сравнение множеств

Множество содержится в множестве, если каждый элементесть элемент. Записывается это следующим способом:. В этом случаеназываетсяподмножеством . Еслии, тоназываетсясобственным подмножеством .

Мощность множества обозначается как. Для конечных множеств мощность – это число элементов. Например,, но. Если, то множестваиназываютсяравномощными.

Иногда в литературе вместо мощности множества используется другой равнозначный ему термин: кардинальное число множества (от латинского cardinalis – главный). Этот термин был введен Георгом Кантором.

4. Операции над множествами

Обычно рассматриваются следующие операции над множествами:

• Объединение: .

• Пересечение: .

• Разность: .

• Симметрическая разность:

.

• Дополнение: .

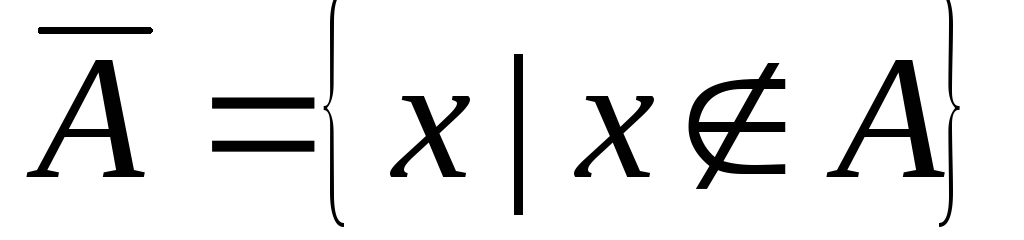Операция дополнения подразумевает некоторый универсум:

.

• Декартово произведение множеств:

.

Декартово произведение двух множеств иесть множество всех упорядоченных пар (x, y), где и.

Пример 5.2. Пусть ,. Тогда

, ,,.

На рис. 5.1 приведены диаграммы Эйлера, иллюстрирующие операции над множествами. Сами исходные множества изображаются геометрическими фигурами (бесконечные множества точек на плоскости), результат выделяется с помощью штриховки.

Рис. 5.1. Диаграммы Эйлера

5. Свойства операций над множествами

Пусть задан универсум . Тогдавыполняются следующие свойства.

1. Инволютивность:

;

2. Идемпотентность:

, ;

3. Коммутативность:

, ;

4. Ассоциативность:

, ;

5. Дистрибутивность:

, ;

6. Поглощение:

, ;

7. Свойство нуля:

, ;

8. Свойство единицы:

, ;

9. Законы де Моргана:

, ;

10. Свойства дополнения:

, ;

11. Выражение для разности:

.

6. Булеан

Множество всех подмножеств множества называетсябулеаном.

Теорема 5.1. Множество из n элементов имеет подмножеств.

Доказательство: Эту теорему можно доказать разными способами (так же, как и многие другие теоремы). Мы докажем ее, используя бинарные представления чисел. Предположим, что мы имеем множество из трех элементов . Каждое подмножество этого множества зашифруем с помощью бинарного кода. Этот код будет состоять из трех бит (по количеству членов исходного множества). Если в рассматриваемом подмножестве присутствует элемент , первому биту кода присваиваем значение единицы, в противном случае – нуля. Если в подмножестве присутствует элемент , второму биту присваиваем значение единицы, в противном случае – нуля. Если в подмножестве присутствует элемент , третьему биту присваиваем значение единицы, в противном случае – нуля. Рассматривая все возможные подмножества исходного множества , включая пустое множество , получим следующий результат.

Как можно видеть, подмножества множества соответствуют восьми числам: 0, 1, …, 7. Мы рассмотрели все бинарные комбинации в пределах трех бит. Как известно, количество таких комбинаций равно .

Применяя данный метод к множеству из четырех элементов, получим количество подмножеств: . Для множества из пяти элементов: . Обобщая эти результаты, приходим к выводу, что множество из n элементов имеет подмножеств.

7. Проблема континуума

Кантор был первым, кто стал рассматривать мощности (кардинальные числа) бесконечных множеств. Мощность счетного множества он обозначил древнееврейской буквой «алеф» с нулевым индексом: . Мощность множества действительных чисел, называемую такжемощностью континуума, обозначил как: . Известно, что кардинальное числобольше кардинального числа. В начале 80-х годов 19 века Кантор высказал гипотезу о том, что ближайшей следующей замощностью является мощность континуума. Обобщенная континуум-гипотеза гласит, что для любого множествапервая мощность, превосходящая мощность этого множества, есть мощность множества всех подмножеств множества. Таким образом,,, …