Случайный выбор из конечного множества

Простейшим и наиболее общим типом распределений, необходимым для практики, является распределение целочисленных случайных величин. Чтобы получить случайное целое число x между 0 и k-1 требуется выполнить одно присваивание x=ku, где 0u<1 является выходом датчика равномерно распределенных на [0; 1) случайных величин.

В более общем случае требуется приписать различным целым числам разные веса. Пусть значение x=x₁ должно получаться с вероятностью p₁ , x=x₂ с вероятностью p₂, ..., x =x_k с вероятностью p_k, где p₁+p₂+...+p_k=1. Можно выработать равномерно распределенное на [0; 1) число U и принять

(15)

Общие методы для непрерывных распределений

Пусть необходимо получить случайную последовательность, имеющую функцию распределения F(x). Если F(x) непрерывна и строго возрастает (так что F(x₁)<F(x₂), если x₁<x₂ ), она принимает все значения между 0 и 1, и существует обратная функция F^-1(u), такая, что если 0<u<1, то u=F(x) тогда когда x=F^-1(u).

Общий способ вычисления случайной величины X с непрерывной строго возрастающей функцией распределения F(x) заключается в том, что полагают

x=F^-1(u). (16)

Поэтому задача сводится к одной из проблем численного анализа для определения хороших методов вычисления F^-1(u) с требующейся точностью.

Однако существует ряд важных рациональных приемов, пригодных для ускорения этого общего метода. Например, если X₁ и X₂ - независимые случайные величины с функциями распределения F₁(x) и F₂(x), то

• max(X₁, X₂) имеет распределение F₁(x)F₂(x),

• min(X₁, X₂) имеет распределение F₁(x)+F₂(x)–F₁(x)F₂(x).

Равномерное распределение

Равномерное распределение на полуинтервале [a; b) определяется соотношением

x=a+(b–a)*u. (17)

Нормальное распределение

Нормальное распределение со средним значением, равным 0, и стандартным отклонением, равным 1 можно моделировать с помощью следующего алгоритма:

1. Выработать два независимых случайных числа u₁ и u₂, равномерно распределенных на [0; 1). Установить v₁=2u₁–1 и v₂=2u₂–1.

2. Присвоить S=v₁²+v₂².

3. Если S≥1, то вернуться к шагу 1.

4. Две независимые нормально распределенные случайные величины x₁ и x₂ получаются из выражений:

. (18)

Другой способ получения нормально распределенной величины X с параметрами 0 и 1 основан на центральной предельной теореме:

x=(u₁+u₂+ ... +u₁₂)–6, (19)

где u₁, u₂, ..., u₁₂ – независимые равномерно распределенные на [0; 1) случайные величины. Недостатком метода является то, что за пределами =2 ( - среднее,  - стандартное отклонение) имеет место сильное расхождение характеристик этого генератора с желаемыми.

Чтобы получить нормально распределенную случайную величину y с параметрами  и ² следует применить преобразование y=+x к нормально распределенной случайной величине x с параметрами =0 и =1.

Экспоненциальное распределение

Для получения экспоненциально распределенной случайной величины x со средним , которое представляет собой время между двумя очередными событиями, следует использовать следующее преобразование (в программах следует избегать случай u=0)

x=-*ln u. (20)

Распределение Пуассона

Оно характеризует число реализаций в единицу времени событий, каждое из которых может произойти в любой момент. Для реализации этого распределения можно использовать следующий алгоритм.

1. Присвоить p=e^-, N=0, q=1.

2. Выработать случайное число u, равномерно распределенное на [0; 1).

3. Присвоить q=qu.

4. Если q≥p, то N=N+1 и вернуться на шаг 2. В противном случае N - искомое случайное число.

9. Универсальные и эмпирические тесты для анализа случайных последовательностей.

Универальные тесты

Критерий χ2. Предположим, что все возможные результаты испытаний разделены на k категорий. Проводится n независимых испытаний (исход каждого испытания не влияет на исход остальных). Пусть p_s - вероятность того, что результат испытания попадет в категорию s, и пусть Y_s – число испытаний, которые действительно попали в категорию s. Сформируем статистику: (3)

Формулу (3) можно преобразовать к виду, более удобному для вычислений: 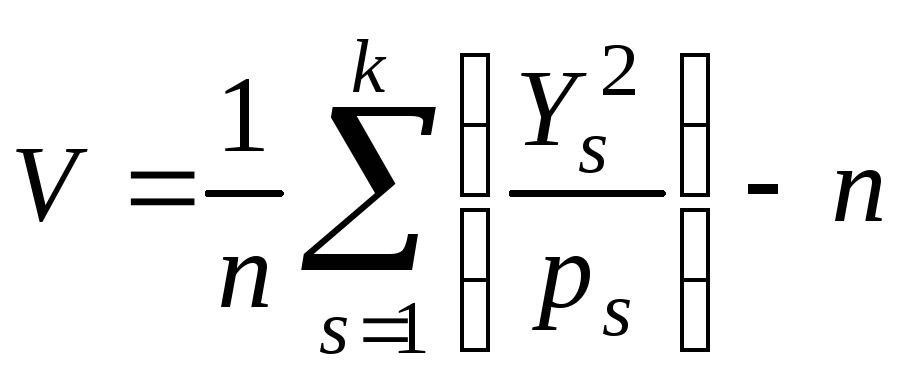(4)

Затем V сравнивается с числом из таблицы для распределения ² при количестве степеней свободы =k–1. Если V меньше значения, соответствующего p=0.99, или больше значения, соответствующего p=0.01, то результаты бракуются как недостаточно случайные. Если p лежит между 0.99 и 0.95 или между 0.05 и 0.01, то результаты считаются "подозрительными". При значениях p, заключенных между 0.95 и 0.90 или 0.10 и 0.05, результаты "слегка подозрительны".

Часто с помощью критерия ² проверяют по крайней мере три разные части исследуемого ряда чисел. Если не менее двух раз из трех результаты оказываются подозрительными, числа отбрасываются как недостаточно случайные. Возникает вопрос о длине n последовательности случайных чисел, которую необходимо выбрать для данного теста. Теоретические расчеты показывают, что достоверные оценки получаются в том случае, когда в каждую из категорий попали не менее 5 испытаний, т.е. выполняется условие Y_s > 4, s=1..k.

Критерий Колмогорова–Смирнова (КС–критерий). Критерий ² применяется в тех случаях, когда результаты испытаний разделяются на конечное число k категорий. Однако часто случайные величины могут принимать бесконечно много значений. В теории вероятностей и математической статистике непрерывные случайные величины описываются с помощью функции распределения: F(x)=p{Xx} (5)

Используя значения x₁, x₂, ..., x_n случайной величины X, можно построить эмпирическую функцию распределения (6)

где .

При увеличении n функции F_n(x) должны все более точно аппроксимировать F(x). КС-критерий можно использовать в тех случаях, когда F(x) не имеет скачков, и он должен указать, насколько маловероятны большие расхождения между F_n(x) и F(x). Для этого используются следующие статистики:

(7)

K_n⁺ показывает, каково максимальное отклонение для случая F_n>F, а K_n^- для F_n<F. Множитель нормирует статистики (7) таким образом, чтобы стандартное отклонение не зависело от n. Далее, как и в случае критерия ², сравнивают значения (7) с табличными и определяют, имеют ли они высокую или низкую значимость.

Формулы (7) не годятся для машинных расчетов, так как требуется отыскать максимальное среди бесконечного множества чисел. Однако, учитывая, что F(x) неубывающая функция, а F_n(x) имеет конечное число скачков, можно определить статистики (7) с помощью следующего алгоритма.

1. Определяются выборочные значения x₁, x₂, ... , x_n.

2. Значения x_i располагаются в порядке возрастания так, чтобы x₁x₂...x_n.

3. Статистики (7) вычисляются по следующим формулам: (8)

Смешанный критерий (КС–критерий и Критерий χ2)

KС-критерием можно пользоваться в сочетании с критерием ², чтобы получить лучшую процедуру отбраковки датчиков, чем правило «два подозрительных из трех проверок». Пусть с помощью критерия ² были независимо обработаны 20 разных участков случайной последовательности, в результате чего были получены значения V₁, V₂, ..., V₂₀. По этим значениям строится эмпирическая функция F₂₀(x) и сравнивается с теоретической функцией распределения, которую можно получить из таблиц распределения ². После определения статистик K₂₀⁺ и K₂₀^- формируется окончательное суждение об исходе проверки последовательности с помощью КС-критерия. В результате часто удается выявить как локальные, так и глобальные отклонения от заданного закона распределения.