
shpory po fany
.docx
№26
Опр:
Пусть
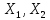 – линейные простр-ва над одним и тем же
полем К. Отображ А:
– линейные простр-ва над одним и тем же
полем К. Отображ А: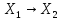 наз. линейным
оператором,
если:
наз. линейным
оператором,
если:
1)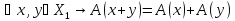 ;
;
2)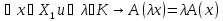 .
.
Если
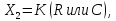 то оператор наз. функционалом
то оператор наз. функционалом
Примеры:
1)Ax=x,
X=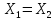 ◄условия 1) и 2) опр-ия очевидны►
◄условия 1) и 2) опр-ия очевидны►
2)Ax=0,x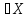 =
= ◄условия 1) и 2) опр-ия очевидны►
◄условия 1) и 2) опр-ия очевидны►
3)Рассм. f: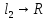 ,
f(x)=
,
f(x)= ,
где x=(
,
где x=(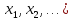 ,
,
f(x+y)=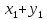 +
+ =f(x)+f(y)
и f(
=f(x)+f(y)
и f(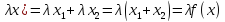
Замечание:
Линейная ф-ция y=kx+b
не является линейным оператором, если
b .
.
Опр: Функционал
f:X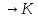 (X
– нормир-ое) наз. огранич., если он
линейный и
(X
– нормир-ое) наз. огранич., если он
линейный и
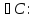 |f(x)|
|f(x)|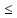 C||x||
C||x||
Пример:
f: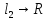 ,
f(x)=
,
f(x)=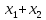 ,
|f(x)|=|
,
|f(x)|=|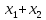 |
|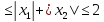 ||x||,
C=2,
||x||=
||x||,
C=2,
||x||=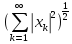
Теорема: Следующие 4 условия равносильны:
1)А: (
(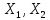 - нормир-ые) ограничены
- нормир-ые) ограничены
2)А непрер-ен в т.О
3)А непрер-ен на
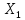 ,
т.е в каждой точке из
,
т.е в каждой точке из
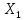
4)А равномерно
непрер-ен, т.е.
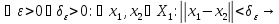 ||A
||A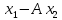 ||<
||<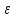
◄Из 4)=>3)=>2)
очевидно. Докажем, что из 1)=>4), т.к.
А-огранич. => ,
то || A
,
то || A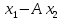 ||=
||= .
Положим
.
Положим
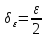
2)=>1) Пусть А –
непрер в т.О, т.е.
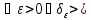 0:
0: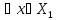 :
||x-0||<
:
||x-0||<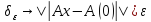
A(0)=A(x-x)=Ax-Ax=0
В силу опред-ия для
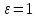
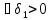 :
:
:
: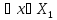 :
||x||<
:
||x||<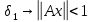 .
Пусть
.
Пусть
 ,
,
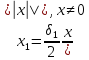 ,
тогда ||
,
тогда ||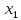 ||=||
||=|| ||=
||=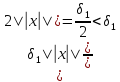 =>||A
=>||A ||<1
или ||A(
||<1
или ||A(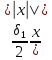 )||=
)||= <1;
||Ax||<
<1;
||Ax||<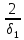 ||x||►
||x||►
№27
Опр:
Пусть А – огранич. оператор из
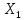 в
в
 (А:
(А: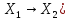
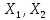 – нормир-ые, число ||A||
наз. нормой
оператора А,
если:
– нормир-ые, число ||A||
наз. нормой
оператора А,
если:
1)||Ax||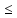 ||A||||x||,
||A||||x||,
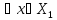
2) :
||A
:
||A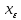 ||>(||A||-
||>(||A||-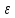 )||
)||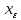 ||,
т.е. ||A||
- наименьшая из констант в нер-ве
огранич-ти.
||,
т.е. ||A||
- наименьшая из констант в нер-ве
огранич-ти.
Теорема: Норма огранич. оператора А может быть вычислена по любой из след-их формул:
1)||A||=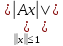
2)||A||=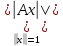
3)||A||=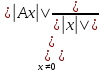
◄Пусть x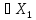 и ||x||
и ||x||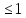 ,
тогда ||Ax||
,
тогда ||Ax||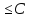 ||x||
||x||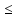 C,
по основной теореме из матана
C,
по основной теореме из матана
 ||A||=
||A||=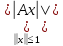 =||A||.
Проверим 1) условие точной верхней грани:
1)||Ax||
=||A||.
Проверим 1) условие точной верхней грани:
1)||Ax||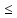 ||A||||x||
||A||||x||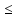 ||A||;
2)
||A||;
2)
 ,
||A
,
||A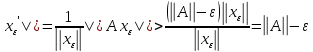 => рав-во 1) доказано. Рав-во 2) следует
из док-ва рав-ва 1). Фор-ла 3) следует из
рав-ва {||Ax||
| ||x||=1}={
=> рав-во 1) доказано. Рав-во 2) следует
из док-ва рав-ва 1). Фор-ла 3) следует из
рав-ва {||Ax||
| ||x||=1}={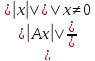 },
т.к.
},
т.к.
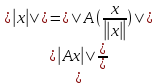 ►
►
Пример:
А:
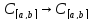 ,
(Ax)(t)=(
,
(Ax)(t)=(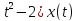 ,
[a,b]=[0,1],
||Ax||=
,
[a,b]=[0,1],
||Ax||=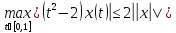
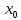 (t)
(t) ,
на [0,1], ||
,
на [0,1], ||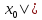 =1
||A
=1
||A ||=2||
||=2||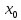 ||
||Ax||
||
||Ax||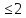 ||x||.
||x||.
Замечание: При нахождении нормы в нер-ве огранич-ти пытаются найти наименьшую константу по возможности и элемент на котором оно превращается в рав-во, тогда эта константа и будет нормой оператора.
№28
Пусть L(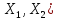 – простр-во лин-ых огранич. операторов
из
– простр-во лин-ых огранич. операторов
из
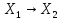 .
Определим в простр-ве L(
.
Определим в простр-ве L(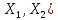 операции сложения и умножения на элементы
из К слева. Пусть А,В
операции сложения и умножения на элементы
из К слева. Пусть А,В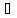 L(
L(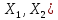 ,
(A+B)(x)=Ax+Bx,x
,
(A+B)(x)=Ax+Bx,x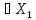 ,
(λA)x=λAx,λ
,
(λA)x=λAx,λ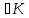 (К
– поле над которым определены
(К
– поле над которым определены
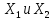 )
)
||(A+B)x||=||Ax+Bx|| ||Ax||+||Bx||
||Ax||+||Bx||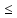 ||A||||x||+||B||||x||=(||A||+||B||)||x||
=> A+В
– ограничены, т.е. (A+B)
||A||||x||+||B||||x||=(||A||+||B||)||x||
=> A+В
– ограничены, т.е. (A+B)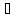 L(
L(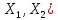 .
Аналогично проверяется, что λA
.
Аналогично проверяется, что λA L(
L( .
Аксиомы лин-го простр-ва будут выполн-ся
в силу опред-ия суммы и произведения
элементов из К операторов и из линейности
.
Аксиомы лин-го простр-ва будут выполн-ся
в силу опред-ия суммы и произведения
элементов из К операторов и из линейности
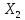 .
Итак L(
.
Итак L(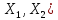 – линейное простр-во. Док-ем, что оно
является нормир-ым простр-ом с нормой
– нормой оператора. Норму А
– линейное простр-во. Док-ем, что оно
является нормир-ым простр-ом с нормой
– нормой оператора. Норму А L(
L(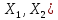 ,
||A||=
,
||A||=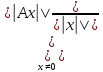 .
Проверим выполнение аксиомы для данной
фор-лы: 1)Пусть ||A||=0
=>
.
Проверим выполнение аксиомы для данной
фор-лы: 1)Пусть ||A||=0
=>
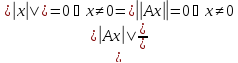 =>Ax=0
=>Ax=0
 => A
– нулевой оператор (А=0); 2)||λA||=
=> A
– нулевой оператор (А=0); 2)||λA||=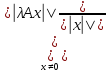 =|λ|||A||.
В силу опр-ия нормы оператора и
подчеркнутого нер-ва L(
=|λ|||A||.
В силу опр-ия нормы оператора и
подчеркнутого нер-ва L(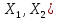 - нормированное простр-во, а => и метрич.
- нормированное простр-во, а => и метрич.
Теорема: Если
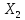 - банохово, то L(
- банохово, то L(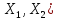 - банохово.
- банохово.
№29
Пусть
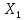 - нормир-ое простр-во. Обозначим Х*=L(X,K)
– мн-во линейных функционалов K=R
или K=ℂ
и наз. сопряж-ым
оператором.
- нормир-ое простр-во. Обозначим Х*=L(X,K)
– мн-во линейных функционалов K=R
или K=ℂ
и наз. сопряж-ым
оператором.
Из теоремы(Если
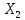 - банахово, то L(
- банахово, то L( – банахово) следует, что Х* - банахово.
Пусть A:
– банахово) следует, что Х* - банахово.
Пусть A: B:
B: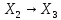 ,
тогда определим оператор (BA)(x)=B(Ax),
BA:
,
тогда определим оператор (BA)(x)=B(Ax),
BA:
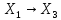 .
Покажем, что если А и В огранич., то ВА –
огранич. ||(BA)x||=||B(Ax)||
.
Покажем, что если А и В огранич., то ВА –
огранич. ||(BA)x||=||B(Ax)|| ||B||||Ax||
||B||||Ax||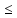 ||B||
||A||
||x||.
||B||
||A||
||x||.
Опр:
Пусть А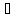 L(
L(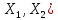 ,
f
,
f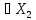 *,
тогда определен (fA)(x)=f(Ax),x
*,
тогда определен (fA)(x)=f(Ax),x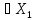 ,
fA:
,
fA: ,
т.е. fA
,
т.е. fA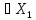 *
тем самым определен оператор А*:
*
тем самым определен оператор А*: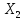 *
*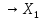 *
по фор-ле А*(f)=fA
(линейность ВА следует из опред-ия
(BA)(x+y)=B(A(x+y))=B(Ax+Ay)=B(Ax)+B(Ay)=(BA)x+(BA)y
*
по фор-ле А*(f)=fA
(линейность ВА следует из опред-ия
(BA)(x+y)=B(A(x+y))=B(Ax+Ay)=B(Ax)+B(Ay)=(BA)x+(BA)y
A* - сопряженный оператору А, Х* - сопряженное простр-во Х.
Утв:
Если А лин-но огранич. оператор из
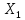 в
в
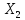 ,
то А* линейно огранич. оператор из
,
то А* линейно огранич. оператор из
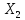 *
в
*
в
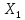 *
и ||A*||
*
и ||A*||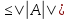 .
.
◄A*f=fA,A*(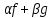 )=(
)=(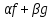 )A.Пусть
х
)A.Пусть
х A*(
A*(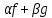 )(x)=(
)(x)=(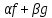 )(Ax)
=(
)(Ax)
=(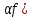 (Ax)+(
(Ax)+(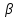 g)(Ax)=
g)(Ax)=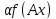 +
+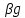 (Ax)=
(Ax)=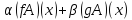 =
=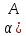 *f)(x)+
*f)(x)+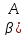 *g)(x)
=(
*g)(x)
=(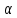 A*f+
A*f+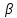 A*g)(x)
=> линейный оператор. Докажем огранич:
||A*f||=||fA||
A*g)(x)
=> линейный оператор. Докажем огранич:
||A*f||=||fA||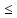 ||A||||f||=>||A*||
||A||||f||=>||A*||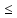 ||A||►
||A||►
Свой-ва сопряженных операторов:
1)(A+B)*=A*+B*
2)( A)*=
A)*=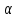 A*
A*
3)(AB)*=B*A*
Эти свой-ва док-ся только исходя из опр. сопряженного оператора, также как линейного сопряженного оператора в утверждении.
№30
Теорема(Банаха-Штейнгауза):
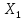 - банахово простра-во,
- банахово простра-во,
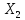 нормир-ое простра-во, М⊂L(
нормир-ое простра-во, М⊂L( и
и
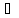 x
x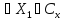 :
||Ax||
:
||Ax||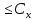
 .
Тогда
.
Тогда
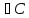 :
||A||
:
||A|| C
C
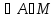 .
.
Следствие:
Если послед-ть {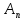 },
},
 L(
L(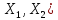 ,
,
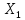 – банахово,
сильно сходится к оператору А, то А
– банахово,
сильно сходится к оператору А, то А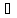 L(
L(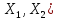 .
.
◄Возьмем М={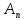 |n
|n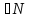 }⊂
L(
}⊂
L(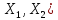 ,
||
,
||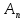 x|||
x|||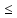 ||A||
||x||.
Т.к.
||A||
||x||.
Т.к.
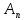 сходится сильно к А, то ||
сходится сильно к А, то ||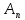 x-Ax||
x-Ax|| 0
при n
0
при n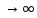 .Для
.Для
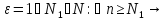 ||
||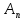 x-Ax||<1,тогда
||
x-Ax||<1,тогда
||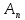 x||
x||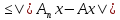 +||Ax||
+||Ax|| ||Ax||+1,n
||Ax||+1,n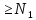 .
.
 ,
||
,
||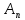 x||
x||
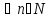 .
По теореме(равномерной огранич)
.
По теореме(равномерной огранич)
 :
||
:
||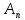 x||
x||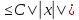 (1). Т.к. ||x||=
(1). Т.к. ||x||=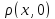 и под знаком расстояния можно перейти
к пределу(см. следствие сжимающих
отображ), то переходя к пределу в нер-ве
(1), получим ||Ax||
и под знаком расстояния можно перейти
к пределу(см. следствие сжимающих
отображ), то переходя к пределу в нер-ве
(1), получим ||Ax||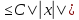 ►
►
Второй принцип функц-го анализа – теорема Ханна-Банаха « о продолжении однородновыпуклого функционала.
№31
Опр:
Пусть А: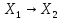 - линейный оператор (
- линейный оператор (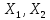 - линейные простр-ва). В:
- линейные простр-ва). В: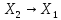 наз. правым(левым)
обратным к
оператору А, если АВ=
наз. правым(левым)
обратным к
оператору А, если АВ= (BA=
(BA=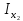 ),
где
),
где
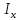 - тождественный оператор в Х:
- тождественный оператор в Х:
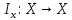 по фор-ле
по фор-ле
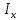 x=x.
Если В является праым(левым) обратным
оператором к А, о он наз. обратным к А и
обознач.
x=x.
Если В является праым(левым) обратным
оператором к А, о он наз. обратным к А и
обознач.
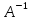
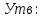 Если А:
Если А:
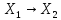 - линейный оператор и
- линейный оператор и
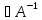 ,
то
,
то
 - линейный оператор.
- линейный оператор.
◄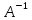 :
: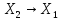 .
Пусть
.
Пусть
 .
Положим
.
Положим
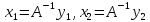 ,
A
,
A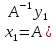 )=(A
)=(A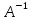 )
)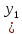 )
=
)
=
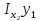 =
=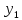 ,
A
,
A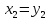 .
.
 =
=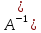 A
A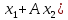 =
=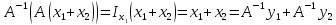 ,
,
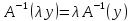 ►
►
Теорема(Банаха об
обратном операторе):
Пусть
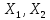 - банаховы простр-ва, А:
- банаховы простр-ва, А: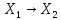 - огранич. оператор и А – биекция. Тогда
- огранич. оператор и А – биекция. Тогда
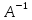 и он ограничен.
и он ограничен.
№32
Понятие спектра
обобщает понятие собственных значений
матрицы. Пусть А:Х Х,
Х – банахово простр-во. Рассм. Ax=λx,λ
Х,
Х – банахово простр-во. Рассм. Ax=λx,λ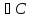 .
Если это урав-ие при некотором
.
Если это урав-ие при некотором
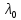 имеет ненулевое решение
имеет ненулевое решение
 ,
то
,
то
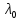 будем наз. собственным
значением
оператора А, а
будем наз. собственным
значением
оператора А, а
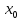 - соответств-им ему собственным
век-ом(А
- соответств-им ему собственным
век-ом(А ).
Если λ – собственное значение оператора
А, то оператор (A-λI)
не имеет обратного, т.е.
).
Если λ – собственное значение оператора
А, то оператор (A-λI)
не имеет обратного, т.е.
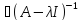 ,
т.к. 2 различных элемента
,
т.к. 2 различных элемента
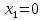 и
и
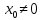 переходят в нуль при таком отображении.
переходят в нуль при таком отображении.
Опр:
λ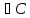 наз. резольвектной точкой оператора А,
если
наз. резольвектной точкой оператора А,
если
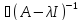 и он ограничен.
и он ограничен.
Мн-во всех резольвектных
точек опер-ра А будем обознач.
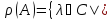 λ – резоль-ой точкой}, а спектром
опер-ра А будем наз.
λ – резоль-ой точкой}, а спектром
опер-ра А будем наз.
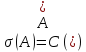 .
Заметим, что собств-ые знач. опер-ра А
являются точками спектра и мн-во всех
собственных значений наз. дискретным
спектром
опер-ра А и обозн.
.
Заметим, что собств-ые знач. опер-ра А
являются точками спектра и мн-во всех
собственных значений наз. дискретным
спектром
опер-ра А и обозн.
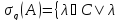 – собств. знач. опера-ра А}, оставшуюся
часть спектра наз. непрерывным
спектром и
обознач.
– собств. знач. опера-ра А}, оставшуюся
часть спектра наз. непрерывным
спектром и
обознач.
 .
.
Теорема:
Если А: Х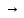 Х
– огранич. оператор, Х – Банахово
простр-во, то
Х
– огранич. оператор, Х – Банахово
простр-во, то
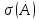 - компактное мн-во, т.е. спектр – замкнутое
и ограниченное мн-во в
- компактное мн-во, т.е. спектр – замкнутое
и ограниченное мн-во в
 и
и
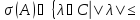 ||A||}.
||A||}.
№33
Опр: Пусть
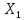 и
и
 - нормир-ые простр-ва А:
- нормир-ые простр-ва А: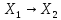 наз. компактным(вполне непрер-ым), если
наз. компактным(вполне непрер-ым), если
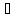 огранич-го мн-ва в
огранич-го мн-ва в
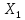 переводим в предкомпактное мн-во в
переводим в предкомпактное мн-во в
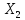 ,
или
,
или
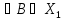 :
В – огранич., А(В) – предкомпактное.
:
В – огранич., А(В) – предкомпактное.
Теорема 1: Для того, чтобы А: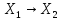 был компактным
был компактным  огранич. послед-ть {
огранич. послед-ть {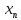 },
},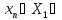 подпослед-ть {
подпослед-ть { }:
{
}:
{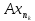 }
фундаментальна.
}
фундаментальна.
◄(=>) Пусть А –
компактно,
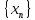 – огранич., {A
– огранич., {A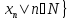 – предкомпактно =>
– предкомпактно =>
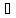 {
{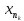 }:{
}:{ }
– фундам-на(из того, что {
}
– фундам-на(из того, что { }
– предкомпактно).
}
– предкомпактно).
(<=) Пусть В –
огранич. и {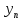 }:
}: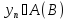 .
По опр. образа А(В)={Ax|x
.
По опр. образа А(В)={Ax|x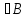 }=>
}=>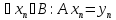 .
Т.к.
.
Т.к.
В – огранич., то {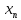 }
– огранич и по условию теоремы
}
– огранич и по условию теоремы
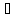 {
{ }:{
}:{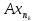 }
фундаментальна или {
}
фундаментальна или {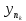 }
– фунд-ная подспослед-ть, где
}
– фунд-ная подспослед-ть, где
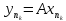 .
Тогда по опр. А(В) – предкомпактно.►
.
Тогда по опр. А(В) – предкомпактно.►
Теорема 2:
А: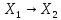 компактен
когда А(В[0,1]) – предкомп-но, где В[0,1] –
единич. шар в
компактен
когда А(В[0,1]) – предкомп-но, где В[0,1] –
единич. шар в
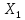
◄(=>)Если А –
компактен,то из компак-ти => A(B[0,1])
– предком-но, где
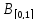 - огранич. мн-во
- огранич. мн-во
(<=) Пусть В –
огранич. мн-во. По опр.
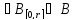 .
C
другой стороны
.
C
другой стороны
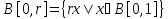 ,
т.к. x=
,
т.к. x=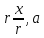 ||
||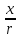 ||=
||= ||x||
||x||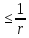 r=1,
A(B)⊂A(B[0,r]).►
r=1,
A(B)⊂A(B[0,r]).►
№34
Примеры:
1)А:
 ,
,

Ax=(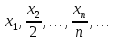 )
)
В силу теор-ы(А: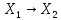 компактенкогда
А(В[0,1]) – предкомп-но,где В[0,1] – единич.
шар в
компактенкогда
А(В[0,1]) – предкомп-но,где В[0,1] – единич.
шар в
 )
необход. Док-ть, что А(В[0,1]) – предкомпактно.
В[0,1]={x
)
необход. Док-ть, что А(В[0,1]) – предкомпактно.
В[0,1]={x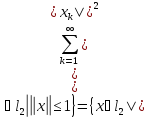 }
}
a) Пусть x [0,1].
Рассм. ||Ax||=
[0,1].
Рассм. ||Ax||= ,
||x||=
,
||x||=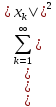
б)
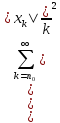 .
Оператор А – компактен.
.
Оператор А – компактен.
2)А: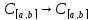 ,
(Ax)(t)=
,
(Ax)(t)= ,
где
,
где
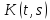 – непрер-на на [a,b]x[a,b]
– непрер-на на [a,b]x[a,b]
a)||Ax||=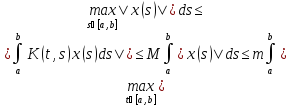 M(b-a),
M(b-a),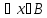 [0,1]
[0,1]
б) По теор. Кантора
для ф-ции нескольких переменных из
непрер-ти Л(ебы) на компакте К следует
её равном-ая непрер-ть на нем, т.е.
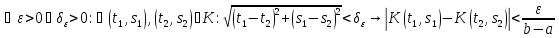 .
|(Ax)(
.
|(Ax)(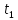 )-(Ax)(
)-(Ax)(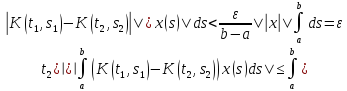 при
|
при
| .
.
Свой-ва компактных опер-ов:
1)Тождественный оператор компактен когда он действует в конечномерном прострав-ве.
2)Предел послед-ти компактных операторов сходящейся по норме, компактен.
3)Если А - компактное,
а В – огранич., то АВ и ВА компактный
опер-ор: (А: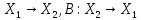 )
)
4)Если А – компактный оператор, то он не может иметь ограниченного обратного, т.е. нуль – точка спектра компактного оператора.
◄Предположим
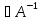 - огранич., по свой-ву 3)А
- огранич., по свой-ву 3)А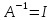 – компактный, что противоречит свой-ву
1) то, что нуль – принадлежит спектру.►
– компактный, что противоречит свой-ву
1) то, что нуль – принадлежит спектру.►
5)Если А - компактный опер-ор, то А* - компактный(А* сопряженный к А).
№35
Опр:
Пусть Х – лин. простр-во над полем К.
Будем говорить, что на Х определено
скалярное произведение, если
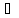 x,y
x,y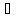 X
поставлено в соотве-ие (x,y)
X
поставлено в соотве-ие (x,y)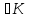 так, что при этом выполнены след. аксиомы:
так, что при этом выполнены след. аксиомы:
1)(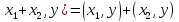 и (λx,y)=
и (λx,y)=
 x,y
x,y ,
,
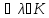 (линейность
по 1-ой координате)
(линейность
по 1-ой координате)
2)(x,y)= (эрмитовость)
(эрмитовость)
3)(x,x)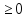 ,
(х,х)=0 =>x=0
,
(х,х)=0 =>x=0
Примеры:
1)X=R,
(x,y)=x y◄аксиомы
очевидны►
y◄аксиомы
очевидны►
2)Х=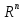 ,
(x,y)=
,
(x,y)=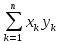 ,
x=(
,
x=(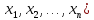 и y=(
и y=(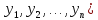 ◄аксиомы очевидны►
◄аксиомы очевидны►
3)Х=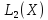 ,
(x,y)=
,
(x,y)=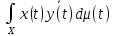 ◄3)свой-во
скалярного произв-ия=>из свой-в интег-ла
Лебега►
◄3)свой-во
скалярного произв-ия=>из свой-в интег-ла
Лебега►
4)Х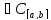 .
Скалярное произв-ие из примера 3) можно
ввести и в
.
Скалярное произв-ие из примера 3) можно
ввести и в
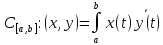 dt.
dt.
Опр: Линейное(векторное) простр-во с введенным на нем скалярным произв-ем наз. предгильбертовым простр-ом.
Утв 2(нер-во
Коши-Буняковского):
Пусть Н – предгильбертово простр-во,
тогда справ-во нер-во |(x,y)|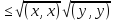
◄(x+λy,x+λy)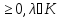 ,
(x+λy,x+λy)=
(x+λy,x)+
,
(x+λy,x+λy)=
(x+λy,x)+ ,
λ:
(x+λy,y)=0,
т.е. (x,y)+λ(y,y)=0
или λ= -
,
λ:
(x+λy,y)=0,
т.е. (x,y)+λ(y,y)=0
или λ= -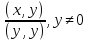 .
При таком λ, (x+λy,x)
.
При таком λ, (x+λy,x)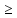 0,
(x,x)+λ(y,x)
0,
(x,x)+λ(y,x)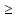 0
или (x,x)
–
0
или (x,x)
–
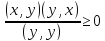 =>(x,y)(y,x)
=>(x,y)(y,x)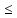 (x,x)(y,y).
По аксиоме 2) (x,y)(y,x)
(x,x)(y,y).
По аксиоме 2) (x,y)(y,x)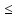 (x,x)(y,y),
(x,y)
(x,x)(y,y),
(x,y)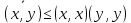 ,
,
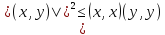 ,
откуда и следует требуемое нер-во.►
,
откуда и следует требуемое нер-во.►
Утв 3(тождество
параллелогр-ма): Пусть Н-предгильбертово
простр-во,
 справедливо тожд-во:
справедливо тожд-во:
 )◄должен
знать►
)◄должен
знать►
