
shpory po fany
.docx
 Пусть
(Х,
Пусть
(Х,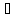 ,
, )
– простр-во с мерой, т.е. на -алгебре
)
– простр-во с мерой, т.е. на -алгебре
 подмнож-ве т. в Х определяется
подмнож-ве т. в Х определяется
 -аддитивная
мера. Обозначим через
-аддитивная
мера. Обозначим через
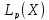 -множ-во
измеримых на множ-ве Х ф-ций, для которых
модуль в р интегрир. на Х,т.е.
-множ-во
измеримых на множ-ве Х ф-ций, для которых
модуль в р интегрир. на Х,т.е.
 ,
,
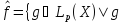 =f
п.в. на Х},
=f
п.в. на Х},
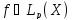 .
.
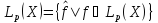 .
Положим p(
.
Положим p(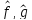 )=
)=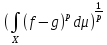 .
Проверим аксиомы метрики:
.
Проверим аксиомы метрики:
1) p(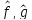 )=0
)=0
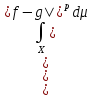
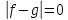 => f=g
п.в. Х
=> f=g
п.в. Х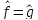 .
В дальнейшем крышечку писать не будем
, но из написанного будет ясно о классе
ф-ций.
.
В дальнейшем крышечку писать не будем
, но из написанного будет ясно о классе
ф-ций.
2)очевидно; 3)аксиома
(3) док-ся с помощью интегрир-ия нер-ва
Минковского: если g,f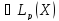 ,
1
,
1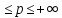 ,
то f+g
,
то f+g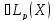 и
и
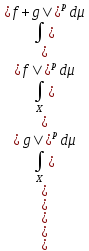 .
Который док-ся с помощью интегрир. нер-ва
Гельдера: Если p,q
.
Который док-ся с помощью интегрир. нер-ва
Гельдера: Если p,q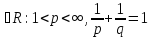 ,
f
,
f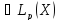 и q
и q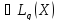 ,
то fg
,
то fg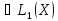 и
и
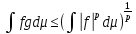 .
Тогда нер-во треугольника для p
сразу следует из интегрального нер-ва
Минковского как и в простр-ве
.
Тогда нер-во треугольника для p
сразу следует из интегрального нер-ва
Минковского как и в простр-ве
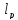 .
.
№15
Опр:
Послед-ть {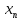 }
}
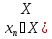 – метрич. простр-во) наз. сходящ-ся, если
– метрич. простр-во) наз. сходящ-ся, если
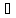 a
a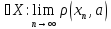 =0:
=0:
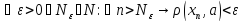 .
.
Опр:
{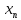 }
в метрич. простр-ве Х наз. фундамен-ой(послед.
Кантера), если
}
в метрич. простр-ве Х наз. фундамен-ой(послед.
Кантера), если
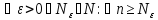 и m
и m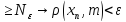 или
или
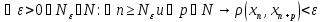
Утв: Всякая сходящаяся послед-ть в метрич. простр-ве Х является фундамен-ой.
◄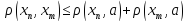 ►
►
Открытым(замкнутым)
шаром обознач.
B(a,r)(B[a;r])
с центром в т.А радиуса r
в метрич. простр-ве (X,p)
наз. B(a,r)={x |
|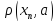 <r}
и
B[a,r]={x
<r}
и
B[a,r]={x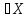 |
| r}
r}
Пример:
X=[0;+ ],
],
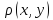 =|x-y|,
B[1,3]=[0;4],
B[0;3.5]=[0;3.5]⊂[0,4]
=|x-y|,
B[1,3]=[0;4],
B[0;3.5]=[0;3.5]⊂[0,4]
Опр:
Множ-во А⊂Х(Х-метрич.
простр-во) наз открытым,
если
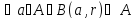 .
.
Утв: Открытый шар является открытым множ-ом.
Опр: Множ-во А⊂Х наз. замкнутым, если Х/А-открыто.
Утв: Следующие утв. Эквивалентны:
1)А-замкнуто(т.е. Х/А – открыто)
2)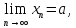
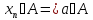
3)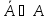
4)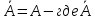 - замыкание множ-ва А, т.е А – множ-во
всех точек прикосновений для А, b
- замыкание множ-ва А, т.е А – множ-во
всех точек прикосновений для А, b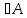 является точкой приложения для А, если
является точкой приложения для А, если
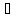 B(b,r)
(r>0)
B(b,r)
B(b,r)
(r>0)
B(b,r)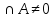 ).
).
№16
Опр:
Отображ. f:
(X, )
)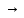 (У,
(У,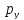 )
наз. непрер. в т.
)
наз. непрер. в т.
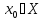 ,
если
,
если
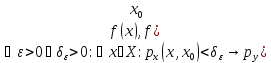 ))<
))<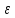
Теорема 1:
f-непрер.
в т.
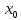
когда
когда
 {
{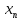 },
},
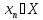 :
:
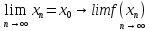 =
=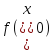 .
.
Следствие:
f-непрер-на
в т.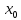
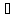 {
{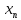 }:
}:
 ,
,
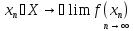
◄=> из теоремы 1
<= Пусть {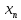 }:
}:
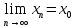 .
Тогда
.
Тогда
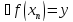 .
Рассм. послед-ть {
.
Рассм. послед-ть {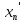 }:
}:
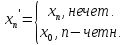 =>
=>
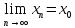 ,
тогда
,
тогда
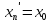 ,
тогда и
,
тогда и
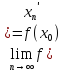 ►
►
№17
Опр: Метрическое простр-во Х наз. полным, если любая фундаментальная послед-ть в Х сходится.
Примеры:
1)R=X
– полное(критерий Коши); 2) – полное; 3)ℂ
- полное; 4)Q=X,
– полное; 3)ℂ
- полное; 4)Q=X,
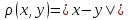 ,
,
 =
=
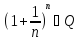 .
Она фундаментальна(сходится в R)
.
Она фундаментальна(сходится в R)
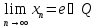 – неполное
– неполное
Теорема:
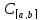 - полное простр-во.
- полное простр-во.
◄Пусть
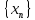 – фундаментальная послед-ть в
– фундаментальная послед-ть в
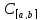 ,
т.е.
,
т.е.
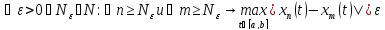 (1).Нам нужно док-ть, что
(1).Нам нужно док-ть, что
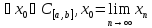 ,т.е.
,т.е.
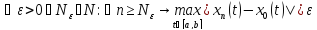 .
.
Утв 1: Последнее
нер-во равносильно условию
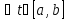 |
|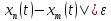 (2). Зафиксируем t
из отрезка [a,b],
тогда числовая после-ть {
(2). Зафиксируем t
из отрезка [a,b],
тогда числовая после-ть {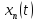 }-
фундаментальна и в силу полноты R
сход-ся, т.е.
}-
фундаментальна и в силу полноты R
сход-ся, т.е.
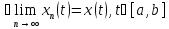 .
Докажем, что получ-ая ф-ция и будет
пределом {
.
Докажем, что получ-ая ф-ция и будет
пределом {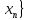 в
в
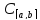 .
Переходя к пределу в (2) при фиксир-ом t
и n,
получим справедливость нерав-ва |
.
Переходя к пределу в (2) при фиксир-ом t
и n,
получим справедливость нерав-ва |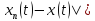 <
<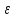 ,
,
 .
Полагая
.
Полагая
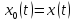 ,
получим, что
,
получим, что
 |
|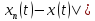 <
<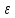 .
Полученное нер-во означает также, что
{
.
Полученное нер-во означает также, что
{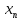 }
равномерно сход-ся на [a,b],
т.к. ф-ции непрерывные.
}
равномерно сход-ся на [a,b],
т.к. ф-ции непрерывные.
И в силу свой-в
равномерно сходящейся после-ти её предел
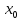 является непрер-ой ф-цией.►
является непрер-ой ф-цией.►
№18
Теорема:
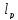 - полное простр-во.
- полное простр-во.
◄Пусть {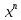 }
– фундаментальная после-ть в
}
– фундаментальная после-ть в
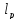 ,
т.е.
,
т.е.
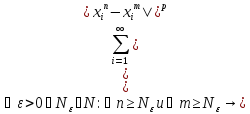 <
<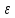 =>
=>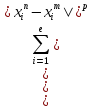 <
<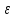 (3).
(3).
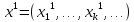

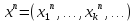
В силу нер-ва
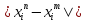 <
<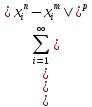
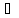 фиксиро-го i
фиксиро-го i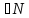 {
{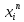 }
будет фунд-ой => сходящ. =>
}
будет фунд-ой => сходящ. =>
 ,
x=
,
x=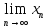 ,
если
,
если
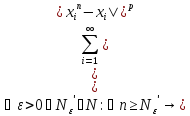 <
<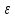 .
Фиксируя в (3) e,i,n
и переходя к пределу при m
.
Фиксируя в (3) e,i,n
и переходя к пределу при m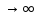 получим, что сумма
получим, что сумма
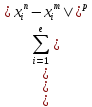 <
<
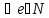 .
Переходя к пределу при e
.
Переходя к пределу при e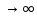 ,
получим
,
получим
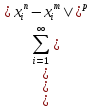 <
<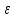 .
Осталось показать, что х
.
Осталось показать, что х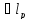 ,
,
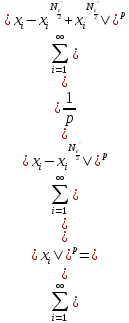 +
+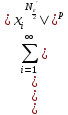 <
<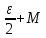 ,
т.к.
,
т.к.
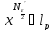 => x
=> x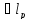 ►
►
Теорема:
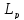 (X)
– полное простр-во.
(X)
– полное простр-во.
№19
Опр:
Отображ. f
из метрич. простр-ва Х(f:X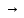 X)
наз. сжимающим,
если
X)
наз. сжимающим,
если
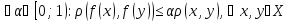
Утв: Любое сжимающее отображение непрерывно(т.е. непрер-но на Х)
◄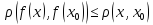 из последнего нер-ва
и т.
из последнего нер-ва
и т.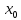 следует непрер-ть.►
следует непрер-ть.►
Опр:
Пусть f:X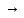 X
X
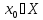 наз. неподвижной
точкой отображ. f,
если f(
наз. неподвижной
точкой отображ. f,
если f(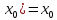 .
.
Теорема(принцип
сжимающих отображений):
Пусть Х-полное метрич. простр-во. Всякое
сжимающее отображ. f:X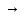 X
имеет и единственную неподвижную точку.
X
имеет и единственную неподвижную точку.
◄ f:X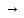 X
X
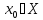 .
Положим
.
Положим
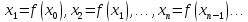 докажем, что {
докажем, что {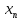 }
является фундам-ной. Введем обознач.
}
является фундам-ной. Введем обознач.
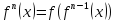 ,
тогда
,
тогда
 (где
n>m)
(где
n>m)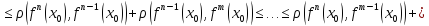
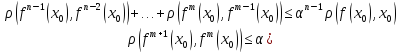 +…+
+…+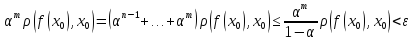 при m
при m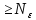 – фунд-ть доказана. Послед-ть {
– фунд-ть доказана. Послед-ть {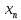 }
фунд-на в силу полноты мн-ва Х. Докажем,
что х-неподвижная точка отображ. f.
В силу опред-ия
}
фунд-на в силу полноты мн-ва Х. Докажем,
что х-неподвижная точка отображ. f.
В силу опред-ия
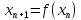 ,
переходя к пределу в послед-нем рав-ве
и пользуясь непрер-тью х, т.е. х –
неподвижная точка отображ. f.
Осталось док-ть, что х – единств-ая
неподвижная точка. Пусть x,y
– две неподвижные точки x=f(x)
и y=f(y),
,
переходя к пределу в послед-нем рав-ве
и пользуясь непрер-тью х, т.е. х –
неподвижная точка отображ. f.
Осталось док-ть, что х – единств-ая
неподвижная точка. Пусть x,y
– две неподвижные точки x=f(x)
и y=f(y),
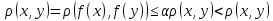 .
Последнее нер-во противоречиво, если
.
Последнее нер-во противоречиво, если
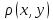 >0.►
>0.►
Следствие:
В условиях теоремы справедливо нер-во
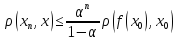 .
.
◄Из док-ва теоремы
следует, что
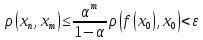 .
Док-ем, что отображ. F:
X
.
Док-ем, что отображ. F:
X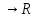 по фор-ле F(x)=
по фор-ле F(x)=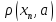 ,
a
,
a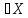 – фиксир., |
– фиксир., |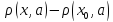 |
|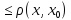 ,
-
,
-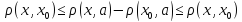 ,
,
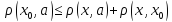 .
Полагая
.
Полагая
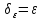 получим непрер-ть =>
получим непрер-ть =>
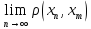 =
=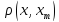 ►
►
№20
Урав-ие вида
x(t)=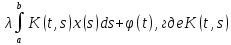 -непрер-ая
на [a,b]x[a,b],
-непрер-ая
на [a,b]x[a,b],
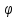 - непрер-ая на [a,b],
K
и
- непрер-ая на [a,b],
K
и
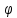 – известные ф-ции, х- неизвестная ф-ция.
наз. урав-ем
Фритгольма 2 рода.
– известные ф-ции, х- неизвестная ф-ция.
наз. урав-ем
Фритгольма 2 рода.
Пусть F(x(t))=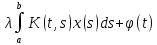 ,
F:
,
F: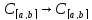 ,
,
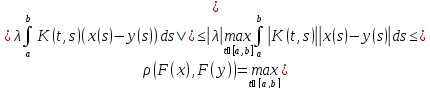 Пусть
M=
Пусть
M=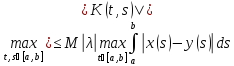 =M
=M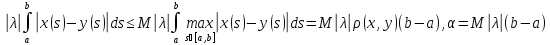 ,
отсюда видно, что отображение F
будет сжимающим при условии, что
,
отсюда видно, что отображение F
будет сжимающим при условии, что
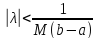 .
.
№21
Опр: Метрич. прост-во (Х, )
наз. компактным, если у всякой
послед-ти
)
наз. компактным, если у всякой
послед-ти
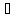 сходящ. подпослед-ть.
сходящ. подпослед-ть.
Утв: Всякое компактное простр-во является полным.
◄{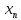 }
– фундам-я, то
}
– фундам-я, то
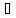 {
{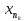 }-сходящ.
к х,
}-сходящ.
к х,
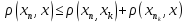 (
(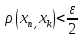 из фунд-ти, а
из фунд-ти, а
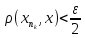 из
из
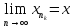 )►
)►
Замечание: Обратное неверно.
Опр:
Метрич. простр-во (Х,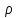 )
наз. предкомпактным, если у любой
послед-ти
)
наз. предкомпактным, если у любой
послед-ти
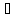 фундам-ая подпослед-ть.
фундам-ая подпослед-ть.
Теорема: Для того, чтобы метрич. простр-во было компактным чтобы оно было предкомпактным и полным.
Опр: Множ-во М⊂Х
наз. компактным(предкомпактным),
если (М, )
– комп-но(предкомп-но), как метрич.
простр-во.
)
– комп-но(предкомп-но), как метрич.
простр-во.
Опр: Мн-во М в метрич. простр-ве наз. огранич., если оно содерж. в некотором шаре.
Теорема(Арцела-Асколи):
M⊂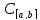 предкомп-но
1)M
– ограничено в
предкомп-но
1)M
– ограничено в
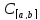 ,
т.е.
,
т.е.
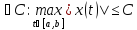 ;
2)M
– равностепенно-непрер-но, т.е.
;
2)M
– равностепенно-непрер-но, т.е.
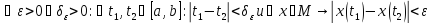
Теорема(критерий
предком-ти в
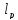 ):
M⊂
):
M⊂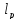 предком-но
когда: 1)M
– огранич., т.е.
предком-но
когда: 1)M
– огранич., т.е.
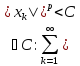 ,
,
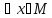 ;
2)
;
2) .
.
№22
Опр:
Пусть Х – метрич. простр-во M⊂X.
A⊂X
наз.
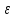 -сетью
для множ-ва М, если
-сетью
для множ-ва М, если
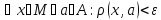 .
.
Пример:
X=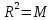 ,
A={(m,n)|m,n
,
A={(m,n)|m,n Z},
A=
Z},
A=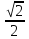 сеть для М.
сеть для М.
Утв:
Если множ-во огранич. в
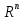 ,
то при
,
то при
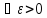 для него
для него
 конечная
конечная
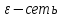 .
.
Опр:
Мн-во в метрич. простр-ве будем наз.
вполне огранич., если для него
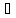 конечная
конечная
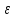 -сеть
для
-сеть
для
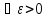 .
.
Утв: Если мн-во вполне ограничено, то оно ограничено.
◄Положим
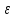 =1,
тогда
=1,
тогда
 - 1-сеть для огранич. М. Возьмем
- 1-сеть для огранич. М. Возьмем
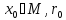 =
=
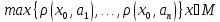 ,
,
 (
(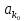 -расстояние
от а до x<1)
-расстояние
от а до x<1)
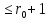 =>M⊂B[
=>M⊂B[ ,
,
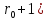 ►
►
Пример:
Рассм. простр-во
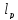 и мн-во точек {
и мн-во точек {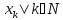 },
где
},
где
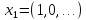
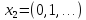
....................

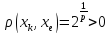 – это мн-во огранич.
Все точки мн-ва М={
– это мн-во огранич.
Все точки мн-ва М={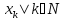 }⊂B[0;1].
Предположим М вполне огранич., т.е. для
}⊂B[0;1].
Предположим М вполне огранич., т.е. для
 найдется конечная
найдется конечная
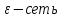 ,
тогда
,
тогда
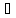 два элемента из М:
два элемента из М:
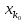 и
и
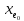 :
:
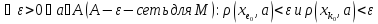 ,
тогда
,
тогда
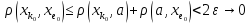 при
при
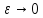 противоречие, => наше предположение
неверно.
противоречие, => наше предположение
неверно.
Теорема(Критерий Хаусдорфа): Для того, чтобы мн-во было предкомпак-ым чтобы оно было огранич.
◄=> Пусть
М-предкомпактно,
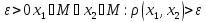 (т.к.
в противном случае {
(т.к.
в противном случае {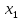 }
будет конечной
}
будет конечной
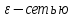 для М),
для М),
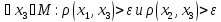 (т.к. в противном случае {
(т.к. в противном случае { }
-
}
-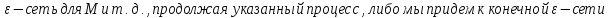 ,
либо получ. послед-ть {
,
либо получ. послед-ть {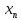 }:
}:
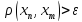 (n
(n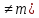 .
Но т.к. m
предкомпактно, то из {
.
Но т.к. m
предкомпактно, то из {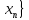 должна извлечься фунд-ая подпослед-ть,
чего быть не может
должна извлечься фунд-ая подпослед-ть,
чего быть не может
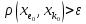 (e
(e ►
►
№23
Опр:
Непустое мн-во Х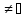 наз. линейным(векторным) простран-ом
над полем К(K=R
или ℂ),
если на этом мн-ве определены 2 операции:
сложение и умножение слева на элементы
из поля К(«+» и «*») так, что выполн.
следующ. условия:
наз. линейным(векторным) простран-ом
над полем К(K=R
или ℂ),
если на этом мн-ве определены 2 операции:
сложение и умножение слева на элементы
из поля К(«+» и «*») так, что выполн.
следующ. условия:
I. 1)x+(y+z)=(x+y)+z;
2)x+y=y+x;
3)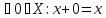
4)
(X – абелева группа по сложению).
II. 1)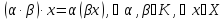
2)1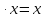 ,
,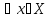
3)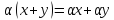 ,
,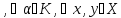
4)
Примеры лин-ых простр-в:
1)X=R, обычные операции сложения, умножения действит-ых чисел.
◄аксиомы I и II следуют из свой-в действит-ых чисел K=R►
2)X= ℂ, ◄аксиомы I и II следуют из комплексных чисел, K=R(или ℂ )►
3)X=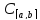 ,
(x+y)(t)=x(t)+y(t),
t
,
(x+y)(t)=x(t)+y(t),
t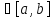 и (λx)(t)=λx(t),
t
и (λx)(t)=λx(t),
t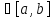
◄аксиомы для случая x+y=y+x следуют из опред-ия и свой-в действит-ых чисел►
4)X=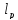 ,
x=(
,
x=(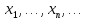 )
y=(
)
y=(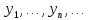 )
x+y=
)
x+y=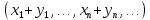 ,
λx=
,
λx=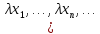 )
)
◄аксиомы следуют
из свой-в действит-ых чисел и опред-ий
операций над числами. То, что сумма 2-ух
элементов из
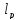 будет
будет
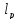 следует из нер-ва Минковского и см.
рассуждение при док-ве.►
следует из нер-ва Минковского и см.
рассуждение при док-ве.►
5)X=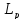 (X),
(X),
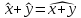 и λ
и λ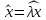
◄аксиомы следуют из опред-ия этих опреаций и свой-в действит-ых чисел►
№24
Опр:
Линейное простр-во Х над полем К наз.
нормированным простр-ом, если на Х
определено отображ. || ||:X
||:X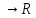 ,
так, что:
,
так, что:
1)||x||=0x=0
2)||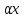 ||=|
||=|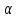 |||x||,
|||x||,
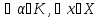
3)||x+y||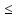 ||x||+||y||(нер-во
треуголь-ка)
||x||+||y||(нер-во
треуголь-ка)
Примеры:
1)X=R,||x||=|x|
2)X=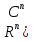 ),
||x||=
),
||x||=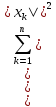
3)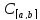 ,
||x||=
,
||x||=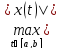
4)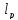 ,
||x||=
,
||x||=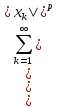
5)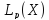 ,
||x||=
,
||x||=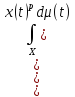
6)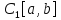 – небанахово, т.к. оно не полно.
– небанахово, т.к. оно не полно.
Свой-ва 1)и 2) очевидны. Нер-во треугольника для примера 1) – очевидно, для 2),4),5) оно превращается в соответствующее нер-во Минковского, а для 3) легко получается из опред-ия max=sup.
Утв:
Если Х-нормированное простр-во, то Х –
метрич. простр-во с метрикой
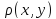 =||x-y||
=||x-y||
◄1)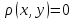 ||x-y||=0x=y
||x-y||=0x=y
2) =||x-y||=||(-1)(y-x)||=||y-x||
=||x-y||=||(-1)(y-x)||=||y-x||
3)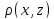 =||x-z||=|x-y+y-z||
=||x-z||=|x-y+y-z||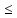 ||x-y||+||y-z||=
||x-y||+||y-z||=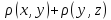 .
Нормир-ое простр-во явля-ся метрич.►
.
Нормир-ое простр-во явля-ся метрич.►
Т.о. все понятия в метрич-их простр-ах имеют смысл в нормир-ых простр-ах.
Опр:
Нормированное простр-во полное,
относительно расстояния
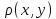 =||x-y||
наз. Банаховым
простр-ом.
=||x-y||
наз. Банаховым
простр-ом.
Опр:
Две нормы
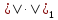 и
и
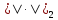 наз. эквивалентными,
если
наз. эквивалентными,
если
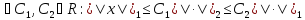 ,
,
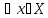 ,
,
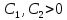
Замечание: Если две нормы эквивалентны, то в соответствующих нормир-ых простр-ах сходящиеся послед-ти одни и те же, компактные мн-ва одни и те же.
№25
Опр:
Пусть
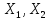 – линейные простр-ва над одним и тем же
полем К. Отображ А:
– линейные простр-ва над одним и тем же
полем К. Отображ А: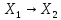 наз. линейным
оператором,
если:
наз. линейным
оператором,
если:
1)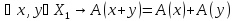 ;
;
2) .
.
Примеры:
1)Ax=x,
X=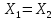 ◄условия 1) и 2) опр-ия очевидны►
◄условия 1) и 2) опр-ия очевидны►
2)Ax=0,x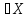 =
=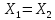 ◄условия 1) и 2) опр-ия очевидны►
◄условия 1) и 2) опр-ия очевидны►
3)Рассм. f: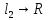 ,
f(x)=
,
f(x)=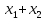 ,
где x=(
,
где x=( ,
,
f(x+y)=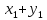 +
+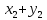 =f(x)+f(y)
и f(
=f(x)+f(y)
и f(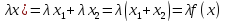
Замечание:
Линейная ф-ция y=kx+b
не является линейным оператором, если
b .
.
Опр:
Пусть
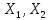 – нормиров-ые простр-ва. Линейный
оператор А:
– нормиров-ые простр-ва. Линейный
оператор А: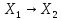 наз. огранич-ым, если
наз. огранич-ым, если
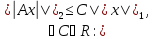
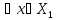 .
.
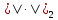 – норма в
– норма в
 и
и
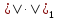 – норма в
– норма в
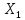 .
.
Примеры:
1)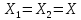 – нормир., Ax=x
||Ax||=||x||,
C=1
– нормир., Ax=x
||Ax||=||x||,
C=1
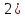 A:
A: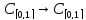 ,
(Ax)(t)=(
,
(Ax)(t)=(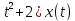
(A(x+y))(t)=( ,
аналогично проверяется 2-ое условие
линейности.
,
аналогично проверяется 2-ое условие
линейности.
||Ax||=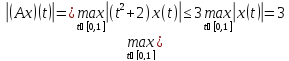 ||x||,
C=3.
||x||,
C=3.
