
shpory po fany
.docx№1 Системы множеств ( кольцо, полукольцо, алгебра, -алгебра и т.д.) Примеры.
Пусть Х-
произвольное мн-во (𝒫(х)-мн-во
всех подмн-в мн-ва Х) или
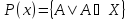
Опр. Система
 наз-ся кольцом ,если 1)
наз-ся кольцом ,если 1) ; 2)
; 2)

Примеры:
1)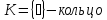 2)
2)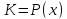
Опр.Симметрической
разностью мн-в А и В обознач.
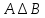 наз-ся мн-во
наз-ся мн-во
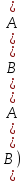
Утв.1(микро)Если
К-кольцо, то тогда
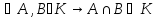 ◄
◄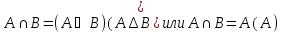 ►
►
Опр.
A=B,
если
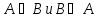
Утв.2
Если К-кольцо,
то
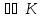 ◄
◄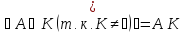 ►
►
Опр.
Сист.
 наз-ся полукольцом,
если 1)
наз-ся полукольцом,
если 1)
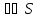 ;
2)
;
2)
 ;
3)
;
3)
Пример: Любое кольцо, явл. полукольцом. Это следует из утв.1,2 и опр. кольца.
Опр. Пусть А(письм)⊂𝒫(x). Кольцо К содержащее А(письм)наименьшее из всех колец сод. А(письм)наз-ся кольцом, порожд. К (А)(письм),т.е.К(А)⊂К, где К-произвольное кольцо содержащее К(А)(письм)-кольцо.
Теор1
К(А)(письм) и единств.
и единств.
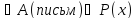 ◄
К(А)(письм)=
◄
К(А)(письм)=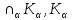 -кольцо,
-кольцо,
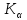
 (А)(письм)
►
(А)(письм)
►
Теор2Пусть
S-полукольцо,
тогда
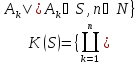
Опр
Кольцо K
наз-ся
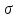 -кольцом,
если 1) К-кольцо 2)
-кольцом,
если 1) К-кольцо 2)

Опр
Сист. К наз-ся -кольцом,
если 1) К-кольцо 2)
Опр
Сист.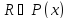 наз-ся алгеброй,
если 1) R-кольцо
2) X
наз-ся алгеброй,
если 1) R-кольцо
2) X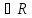
Опр
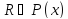 наз-ся
наз-ся
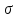 -алгеброй
, если 1)
-алгеброй
, если 1)
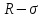 -кольцо
2) R-алгебра
-кольцо
2) R-алгебра
Опр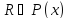 наз-ся
наз-ся
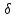 -алгеброй
, если 1)
-алгеброй
, если 1)
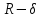 -кольцо
2) R-алгебра
-кольцо
2) R-алгебра
Утв
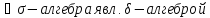 ◄Пусть R.
В силу опр. дост. док-ть, что R-
◄Пусть R.
В силу опр. дост. док-ть, что R-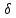 -кольцо.
-кольцо.
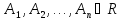 .
Y=
.
Y= .
.
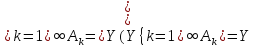
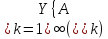 ,
т.к.R-
,
т.к.R-
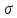 -кольцо
►
-кольцо
►
Прим:
-сист. интервалов
и их счётных объединений. Наименьшее
из -колец содержащих сист.
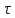 наз.
наз.
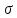 -алгеброй
борелевских мн-в.
[a,b)=
-алгеброй
борелевских мн-в.
[a,b)=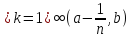
№2 Определение и свойства меры ( доказать любые 3 свойства меры ).
Опр
Пусть S-полукольцо.
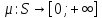 (не
равная тождественно +
(не
равная тождественно + ,т.е.
,т.е.
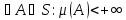 )
назовём мерой на S,
если она аддитивна
)
назовём мерой на S,
если она аддитивна
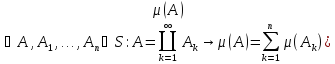 -наз-ся
мерой мн-ва А.
-наз-ся
мерой мн-ва А.
Опр
Мера
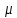 на S
наз-ся
на S
наз-ся
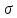 -аддитивной(или
счётно-аддит.), если
-аддитивной(или
счётно-аддит.), если
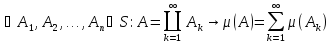
Опр
Пусть
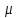 -мера
на полукольце S.
Мера
-мера
на полукольце S.
Мера
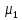 опред-ая на полукольце
опред-ая на полукольце
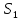 наз-ся продолжением
меры
наз-ся продолжением
меры
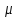 ,
если : 1) S⊂
,
если : 1) S⊂ 2)
2)

Теор
Пусть -мера на полукольце S,
тогда
 и единст. Продолжение
и единст. Продолжение
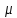 на К(S)◄
на К(S)◄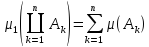 ►
►
Св-ва
меры: Пусть
-мера на полукольце S,
а
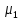 -её
продолжение на K(S).
-её
продолжение на K(S).
1)
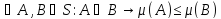 ◄B=A
◄B=A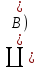 ;
;
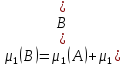 ►
►
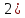 Пусть
Пусть
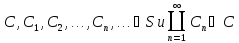 .
Тогда
.
Тогда
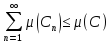 .
◄
.
◄ ;
;
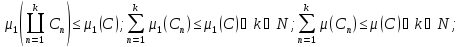 Переходя к пределу при
Переходя к пределу при
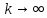 получим
требуемое нер-во►
получим
требуемое нер-во►
3)
Пусть
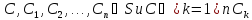 .
Тогда
.
Тогда
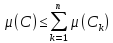 ◄
◄ ►
►
4)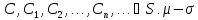 -аддитивна
⇔
(
-аддитивна
⇔
(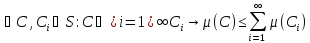 )
)
5)
Пусть
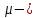 -аддит.
Мера на полукольце S
и
-аддит.
Мера на полукольце S
и
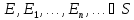 ,
причём
,
причём
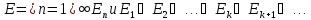 Тогда
Тогда
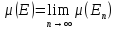
№3 Определение и свойства внешней меры
Опр Пусть
S-полукольцо и m- -аддитивная
мера на S(S
-аддитивная
мера на S(S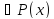 ).
).
Внешней
мерой мн-ва A⊂X
наз-ся точная нижняя грань
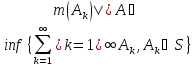 .
.
Если А можно
покрыть счётным объединением полукольца
и хотя бы одна из сумм
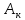 -конечна.
В противном случае, полагают внешнюю
меру мн-ва
-конечна.
В противном случае, полагают внешнюю
меру мн-ва
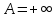
Св-ва меры:
1)
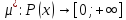
2) (счётная
полуаддит-ть)
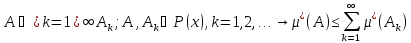
3) Если
A⊂B,
 ,
то
,
то
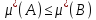 ◄А⊂В⊂
◄А⊂В⊂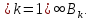 Покрытие мн-ва А не меньше, чем покрытие
мн-ва В, поэтому из опр. внешней меры
мн-ва А, точная нижняя грань берется
возможно по более широкому числовому
мн-ву►
Покрытие мн-ва А не меньше, чем покрытие
мн-ва В, поэтому из опр. внешней меры
мн-ва А, точная нижняя грань берется
возможно по более широкому числовому
мн-ву►
4)
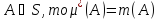 ◄Пусть А⊂
◄Пусть А⊂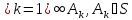 .
Т.к. m
.
Т.к. m
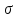 -аддитивна,
то m(A)
-аддитивна,
то m(A)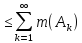 ►
►
№4 Лебеговское продолжение меры. Измеримые множества.
Опр Пусть
S-полукольцо и m-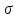 -аддитивная
мера на S(S
-аддитивная
мера на S(S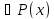 ).
).
Внешней
мерой мн-ва A⊂X
наз-ся точная нижняя грань
 .
.
Если А можно
покрыть счётным объединением полукольца
и хотя бы одна из сумм
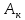 -конечна.
В противном случае, полагают внешнюю
меру мн-ва
-конечна.
В противном случае, полагают внешнюю
меру мн-ва
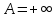
Опр
Мн-во
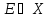 наз-ся измеримым
по Лебегу,
если
наз-ся измеримым
по Лебегу,
если
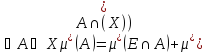 .
Обозначим мн-во всех измеримых мн-в по
Лебегу через
.
Обозначим мн-во всех измеримых мн-в по
Лебегу через
 -мн-во
всех измеримых по Лебегу мн-в.
-мн-во
всех измеримых по Лебегу мн-в.
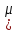 -Лебеговское
продолжение m.)
-Лебеговское
продолжение m.)

Теор(важная)
1)
M(готич)-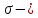 алгебра
2)
алгебра
2)
 -аддит.
мера на M(готич)
3)
-аддит.
мера на M(готич)
3)
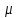 -продолжение
меры m
на M(готич).
Из пункта 3) следует, что S⊂
-продолжение
меры m
на M(готич).
Из пункта 3) следует, что S⊂ M(готич)
M(готич)
№5 Мера Лебега на прямой.
Опр
Пусть S-полукольцо.
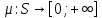 (не
равная тождественно +
(не
равная тождественно +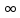 ,т.е.
,т.е.
 )
назовём мерой на S,
если она аддитивна
)
назовём мерой на S,
если она аддитивна
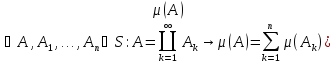 -наз-ся
мерой мн-ва А.
-наз-ся
мерой мн-ва А.
Опр
Мера
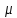 на S
наз-ся
на S
наз-ся
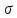 -аддитивной(или
счётно-аддит.), если
-аддитивной(или
счётно-аддит.), если
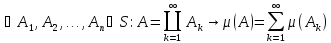
Прим(важный):
Пусть S={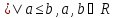 }.
Положим
}.
Положим
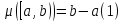 .Покажем,
что ф-ла (1) задаёт меру на S.
1)
.Покажем,
что ф-ла (1) задаёт меру на S.
1)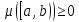 2) Пусть
2) Пусть
 .
Очевидно, что можно считать, что полуинт-лы
.
Очевидно, что можно считать, что полуинт-лы
![]()
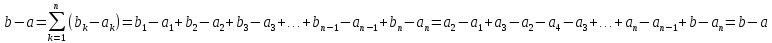 .
Итак, аддит-ть доказана. Меру, определяемую
ф-ой (1) наз-ют мерой
Лебега на прямой.
.
Итак, аддит-ть доказана. Меру, определяемую
ф-ой (1) наз-ют мерой
Лебега на прямой.
№6.Измеримые функции и их свойства.
Теор
Пусть ( )-пр-во
с мерой, где X-произвольное
мн-во.
)-пр-во
с мерой, где X-произвольное
мн-во.
 -алгебра
подмн-ва X
-алгебра
подмн-ва X
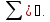
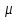 -полная
-аддитивная мера на
-полная
-аддитивная мера на

Опр
Действительнозначную
ф-ию
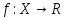 наз-ют измеримой
на мн-ве
наз-ют измеримой
на мн-ве
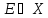 ,
если E-измеримо
(т.е.
,
если E-измеримо
(т.е.
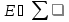 )
и
)
и
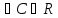 {
{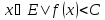 }-измеримо
}-измеримо
Утв
Композиция
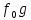 ,
т.е.
,
т.е.
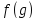 измерима, если
измерима, если
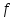 -непр.,
а
-непр.,
а
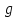 -измерима
-измерима
Теор1
Если
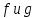 измеримы на Е, то
измеримы на Е, то
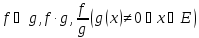 измеримы на Е и
измеримы на Е и
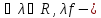 измерима
на Е. ◄???►
измерима
на Е. ◄???►
Теор2
Пусть { }
}
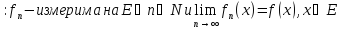 .
Тогда f
измерима на Е ◄???►
.
Тогда f
измерима на Е ◄???►
Опр
Мера
 -мера
на полукольце S
наз-ся полной
мерой, если
из того, что
-мера
на полукольце S
наз-ся полной
мерой, если
из того, что
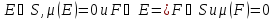
Утв Лебеговское продолжение меры- полная мера
Опр
Пусть Е-измеримое
мн-во. Будем говорить, что некот. св-во
Р(х),x выполняется
почти всюду
на Е, если мера мн-ва
выполняется
почти всюду
на Е, если мера мн-ва
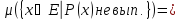 0
0
Опр Ф-ии равные почти всюду(п.в.) на Е наз-ся эквивалентными на Е
Утв
Эквивалентные
на Е ф-ии измеримы или неизмеримы
одновременно. Посл-ть
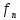 сх-ся п.в. на Е к f,
если
сх-ся п.в. на Е к f,
если

Утв Если посл-ть измеримых на Е ф-ий сх-ся п.в. на Е к f, то f-измерима
Теор.(Егорова):
Если
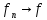 п.в. на Е (
п.в. на Е (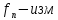 ),
то
),
то
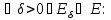 1)
1)
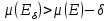 2)
2)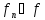 (на
(на
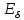 )
)
№7. Интеграл Лебега от неотрицательной функции и его свойства (доказать любые 3 свойства).
Опр f
измерима на E и неотриц.
(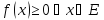 ).
Число
).
Число
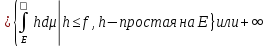 ,
если указанное мн-во неогр. Или один из
интегралов
,
если указанное мн-во неогр. Или один из
интегралов
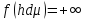 наз-ся интегралом от ф-ии f
по мн-ву Е
наз-ся интегралом от ф-ии f
по мн-ву Е
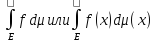
Св-ва:
1) Если
f=g
п.в. на Е, f,g-измеримы
на Е и неотриц-ны, тогда
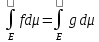
◄Это свой-во сначала док-ся простых ф-ций. Мн-ва, которые стоят в опр. интеграла для f и g одинаковые, поэтому sup у них тоже одинаковые►
2) Если f
и g –измеримы
и неотриц. На Е, причём
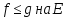 ,
то
,
то
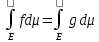 ◄Следует
из опр►
◄Следует
из опр►
3)
Если f
измерима и неотриц. на Е и k>0,
то
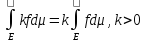
4)
Если f,g
–измеримы на
Е и неотриц, то
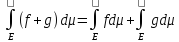
5)
Отображ.
 -аддит-ая
мера на
-аддит-ая
мера на
 ,
т.е. если
,
т.е. если
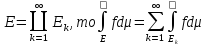
6)(Нер-во
Чебышева)
Пусть f
–неотриц.,
измерима на Е и
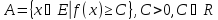 .
Тогда
.
Тогда
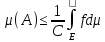 ◄Рассм.
хар-ую ф-цию мн-ва
◄Рассм.
хар-ую ф-цию мн-ва
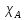 ,
тогда f
,
тогда f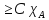 на Е. По свой-ву 2)
на Е. По свой-ву 2)
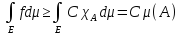 ►
►
7)
Пусть f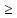 0
на Е и измерима
на Е. Тогда
0
на Е и измерима
на Е. Тогда
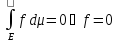 (п.в.
на Е)
(п.в.
на Е)
№8. Интеграл Лебега от произвольной измеримой функции и его свойства (доказать любые 3 из них).
Пусть
f-измерима на Е.
Рассм. ф-ии
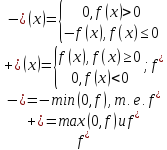 . Очевидно
. Очевидно
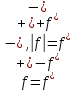
Опр Ф-ия
f наз-ся интегрируемой
на Е, если f измерима
на Е и
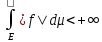 .
Очевидно, если f
интегрируема на Е, то
.
Очевидно, если f
интегрируема на Е, то
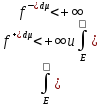
Опр Если
f-интегр-ема на Е,
то число
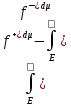 наз-ся интегралом Лебега от f
по мн-ву Е и обозн.
наз-ся интегралом Лебега от f
по мн-ву Е и обозн.
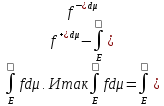
Св-ва:
1) Если ф-ии f и g-интегрируемы на Е и равны п.в. на Е, то интегралы их равны на Е.
2) Если
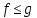 на Е, то
на Е, то
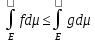 ◄Очевидно,
◄Очевидно,
 .Тогда
.Тогда
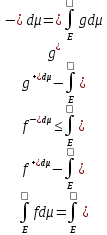 ►
►
3) Если f
и g интегрируемы на
Е, то
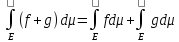
4) Если f
инт-ема на Е и
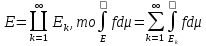
5)
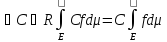
6)
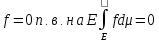 .
Обратное неверно :
.
Обратное неверно :
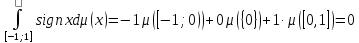
№9. Предельный переход под знаком интеграла Лебега (доказать одну из теорем о предельном переходе).
Теор(Лебега
о мажорированной сх-ти): Пусть {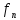 }
посл-ть интегр-емых на Е ф-ий:
}
посл-ть интегр-емых на Е ф-ий:
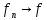 п.в. на Е и
п.в. на Е и
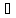 ф-ия -интегр-емая на Е : |
ф-ия -интегр-емая на Е : |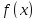 |
|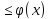 п.в. на Е. Тогда f
интегр-ема на Е и
п.в. на Е. Тогда f
интегр-ема на Е и
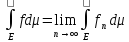
Теор(Бетто-Леви):
): Пусть {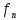 }-посл-ть
интегр. на Е ф-ий и
}-посл-ть
интегр. на Е ф-ий и
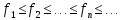 причём
причём
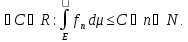 Тогда п.в. на Е
Тогда п.в. на Е
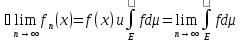
№10. Сравнение интеграла Лебега с интегралом Римана.
Теор.(сравн.
инт. Лебега с инт. Римана): Если ф-ия f
интегрируема по Риману на [a;b],
то f-
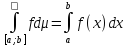
Теор.(связь несобст. инт-ла Римана и инт. Лебега): Для того, чтобы сущ-ал интеграл Лебега от ф-ии интегр-емой по Риману в несобственном смысле ⇔ чтобы несобст-ый инт-ал Римана абсол. сх-лся, при этом инт. Римана и Лебега совпадали.
№11
Утв 1: Пусть p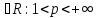 и q
и q ,
тогда
,
тогда
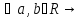 нер-во: ab
нер-во: ab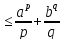 (1), a
(1), a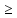 0
и b
0
и b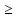 0
0
◄Пусть
 ,
0<x<+
,
0<x<+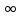 ,
,
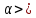 0,
0,
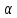 <1.
<1.
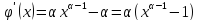
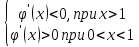 =>
x=1
– т. максимума =>
=>
x=1
– т. максимума =>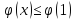
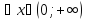 или
или
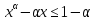 ,
,
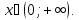
x=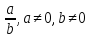 (при
a
и(или) b
= 0 нер-во очевидно),
(при
a
и(или) b
= 0 нер-во очевидно),
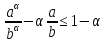
 b
b
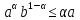 +
+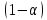 b,
b,
 ,
,
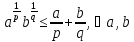 >0.
>0.
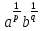 <
<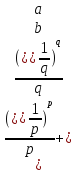 ,
,
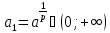 ,
если a
,
если a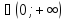 ,
,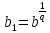 ►
►
№12
Утв 2(нер-во Гельдера): Пусть p,q :
:
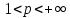 ,
,
 .
Тогда
.
Тогда
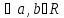 (т.е.
(т.е.
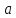 =
=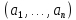 ,
b=
,
b=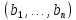 )
выполн. нер-во:
)
выполн. нер-во:
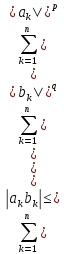 (2)
(2)
◄Шаг1:
Докажем, что нер-во (2) верно при условии,
что
 =1
(3).
=1
(3).
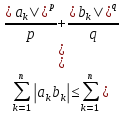 =
=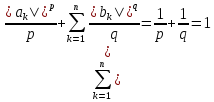 .
При условии (3) нер-во (2) доказано. Шаг2:
Заметим, что если нер-во (2) верно для a
и b,
то оно врено и для
.
При условии (3) нер-во (2) доказано. Шаг2:
Заметим, что если нер-во (2) верно для a
и b,
то оно врено и для
 =
= и
и
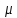 b=
b= .
Пусть теперь a и и такие,
что усл. (3) не выпол-ся. Положим
.
Пусть теперь a и и такие,
что усл. (3) не выпол-ся. Положим
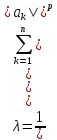 ,
,
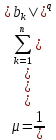 , тогда для
, тогда для
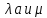 b
выполнено усл. (3) и => для них справедливо
рав-во (2) и оно примит вид:
b
выполнено усл. (3) и => для них справедливо
рав-во (2) и оно примит вид:
 ►
►
№13
Утв 3(нер-во
Минковского): Пусть
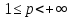 ,
p
,
p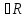 .
Тогда
.
Тогда
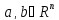 вып. нер-во
вып. нер-во
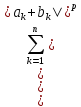
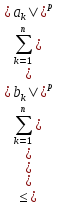 (4)
(4)
◄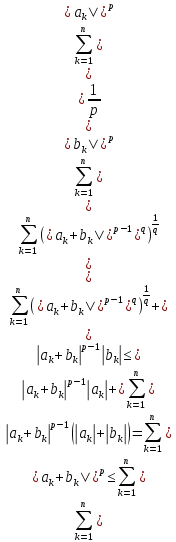 =
=
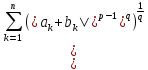 .
.
(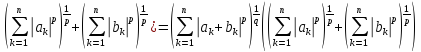 .
.
 (4*)
(4*)
Из (4*) и следует
требуемое нер-во, если разделить обе
части на
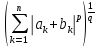 .
При р=1 мы не могли применить нер-во
Гельдера, но в этом случае нер-во
Минковского следует из нер-ва для модуля.
►
.
При р=1 мы не могли применить нер-во
Гельдера, но в этом случае нер-во
Минковского следует из нер-ва для модуля.
►
Следствие(нер-ва
Минковского): При условиях утв. 3
справедливо нер-во:
 (5).
(5).
Следствие получается
из нер-ва (4) переходя к пределу при n .
Обоснование этого предельного перехода
следует из свой-в пределов, опр. суммы
ряда и непрерывности.
.
Обоснование этого предельного перехода
следует из свой-в пределов, опр. суммы
ряда и непрерывности.
№14
Опр: Пусть Х-произвольно множ-во,
отображение
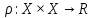 наз. метрикой на Х, если
наз. метрикой на Х, если
 соответствует действительное число
соответствует действительное число
 :
выполнены следующ. аксиомы метрики:
:
выполнены следующ. аксиомы метрики:
1)
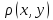 =0
x=y; 2)
=0
x=y; 2)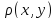 =
=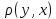 ;
3)
;
3) – нер-во треуг-ка.
– нер-во треуг-ка.
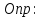 Непустое мн-во Х с заданной на нем
метрикой наз. метрич. простран-ом (Х,
Непустое мн-во Х с заданной на нем
метрикой наз. метрич. простран-ом (Х,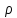 )
или Х.
)
или Х.
Примеры:
1)Х=R,
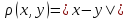 ;
(аксиомы метрики очевидны)
;
(аксиомы метрики очевидны)
2)Х= ,
,
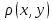 =|x-y|;
=|x-y|;
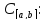 Через
Через
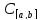 будем обознач. простран-во, непрерывных
на [a;b]
действительно значных или компактно
значных ф-ций, т.е.
будем обознач. простран-во, непрерывных
на [a;b]
действительно значных или компактно
значных ф-ций, т.е.
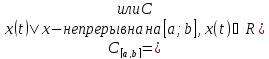 .
Положим Х=
.
Положим Х=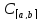 ,
,
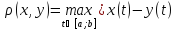 |(сущ-ие
|(сущ-ие
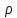 следует из непрерывности ф-ции и т.
Вейерштрасса). Проверим аксиомы метрики:
следует из непрерывности ф-ции и т.
Вейерштрасса). Проверим аксиомы метрики:
1)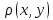 =0
=0
 |=0
|x(t)-y(t)|=0
|=0
|x(t)-y(t)|=0
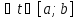 x(t)=y(t)
x(t)=y(t)
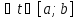 x=y.
x=y.
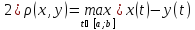 |=
|=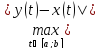 =
=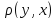
3)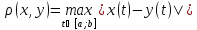 =
=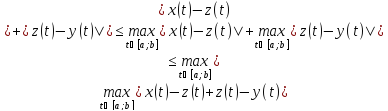 =
= .
.
Значит
 - метрич. простр-во. В дальнейшем если
не указано иное, будем под понимать
метрич. простр-во с рассмот-ой выше
метрикой, которую также наз. равномерной
метрикой.
- метрич. простр-во. В дальнейшем если
не указано иное, будем под понимать
метрич. простр-во с рассмот-ой выше
метрикой, которую также наз. равномерной
метрикой.
 Обозначим через
Обозначим через
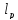 - мн-во всех последов-ей действит-ых или
комплексных чисел, для кот-ых ряд,
составляется из равных степеней
абсолютных величин, сходится, т.е.
- мн-во всех последов-ей действит-ых или
комплексных чисел, для кот-ых ряд,
составляется из равных степеней
абсолютных величин, сходится, т.е.
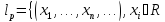
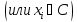 и
и
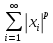 <+
<+ (p
(p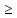 1)
1)
X=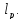 Пусть x
Пусть x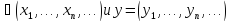 ,
,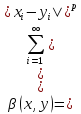 .
Проверим аксиомы метрики: 1)
.
Проверим аксиомы метрики: 1)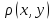 =0
=>
=0
=>
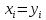
 ;
2)очевидно; 3)Положим в нер-ве Минковского
;
2)очевидно; 3)Положим в нер-ве Минковского
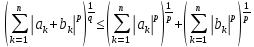
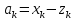 и
и
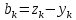 ,
тогданер-во треугольника сразу следует
из нер-ва Минковского. Т.о. пара (
,
тогданер-во треугольника сразу следует
из нер-ва Минковского. Т.о. пара (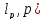 образуют метрич. простр-во, кот-ое будем
наз.
образуют метрич. простр-во, кот-ое будем
наз.

