4.4 Поле объемно заряженного шара

Объемная плотность - на единицу объема.

Шар с радиусом Rс общим зарядомqзаряжен равномерно с объемной плотностью.

Учитывая симметрию можно показать, что вне шара:

()

Внутри же шара поверхность будет другой. Сфера радиуса r’Rравномерно охватывает заряд:

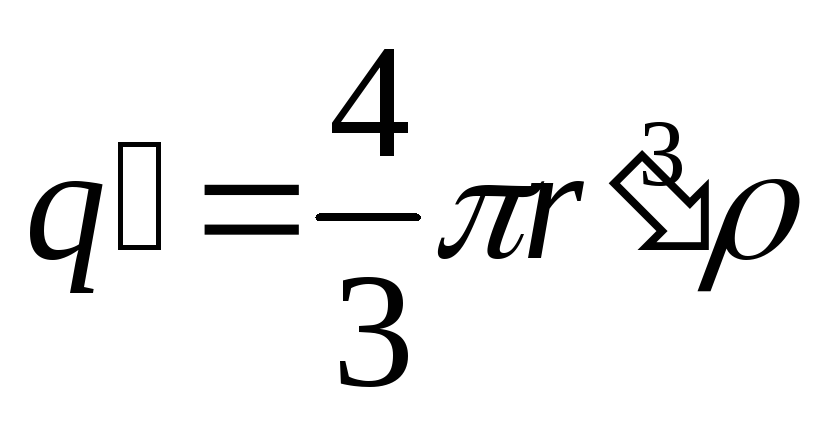
Тогда по теореме Гаусса

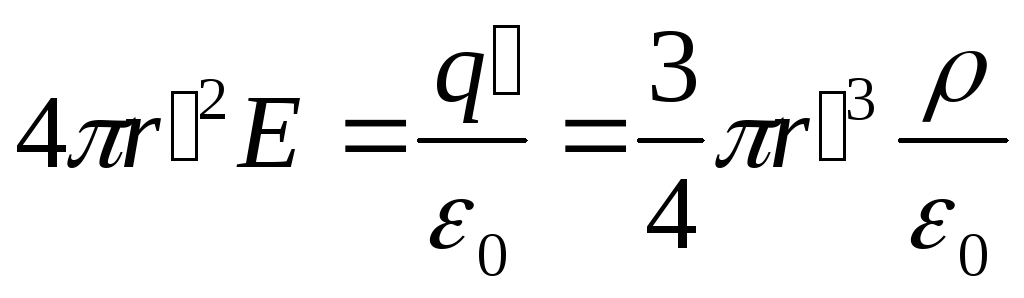
Учитывая что 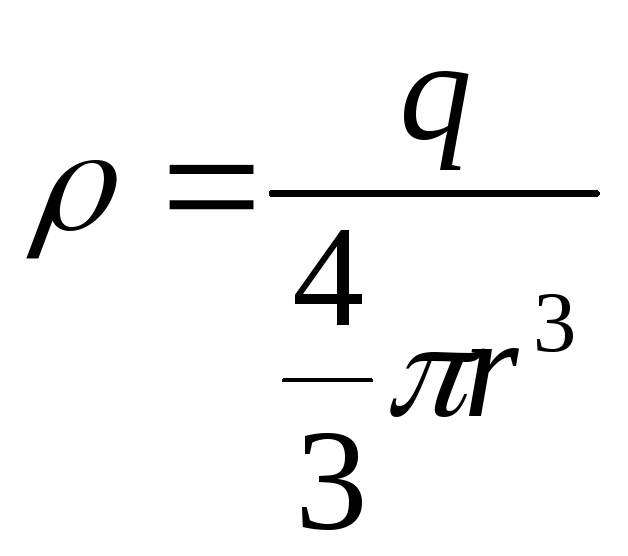, получим:

()

5.1 Электрическое поле в диэлектриках

5.2 Вектор электрического смещения (индукция)

5.3 Условия на границе двух диэлектриков

5.4 Проводники во внешнем поле

5.5 Емкость. Конденсаторы

5.1 Электрическое поле в диэлектриках

Вещества, не способные проводить ток называются диэлектриками. Диэлектрик состоит из атомов и молекул. Т.к. положительный заряд всех ядер молекулы равен суммарному заряду электронов, то молекула в целом электрически нейтральна.

Если заменить положительные заряды ядер молекул суммарным зарядом +Q, находящемся в центре тяжести положительных зарядов, а заряд всех электронов суммарным отрицательным зарядом–Q, находящимся в центре тяжести отрицательных зарядов, то молекулу можно рассматривать как электрический диполь с электрическим моментом:

У симметричных молекул (Н₂, О₂, N₂) центры тяжести положительных и отрицательных зарядов в отсутствие внешнего электрического поля совпадают и дипольный момент.

У несимметричных молекул (Н₂О, СО, НCl) центры не совпадают и даже в отсутствие внешнего электрического поля. Молекулы таких диэлектриков называютполярными.

При помещении молекулы во внешнее электростатическое поле она поляризуется, т.е. приобретает дипольный момент Р.

P_V=p_i,

где p_i – дипольный момент одной молекулы.

Для молекулы:

где -поляризуемость молекулы.

Поляризация в данной точке:

Эта величина называется поляризованностью диэлектрика.

где æ –диэлектрическая восприимчивость.

5.2 Вектор электрического смещения (индукция)

Заряды, входящие в состав молекул, связанные. Поле в диэлектриках – суперпозиция полей, создаваемых связанными зарядами и сторонними (свободными).

 - объемная плотность свободных зарядов

’ – объемная плотность связанных зарядов.

Мы не можем определить , т.к. не знаем’. Поэтому вводят величину, источником которой являются только сторонние заряды.

Плотность связанных зарядов, используя теорему Остроградского-Гаусса, можно записать:

;

;

ææ

1+ æ=- диэлектрическая проницаемость

5.3 Условия на границе двух диэлектриков

Рассмотрим связь между векторами ина границе раздела двух однородных изотропных диэлектриков с диэлектрическими проницаемостями₁ и₂, при отсутствии на границе свободных зарядов (= 0).

Построим вблизи границы раздела диэлектриков небольшой замкнутый прямоугольный контур

Рис.16

При b  0, получим:

Е_1х = Е_2х

но D =  ₀ E, тогда:

Рассмотрим цилиндр высотой h:

, по  = 0, то

Ф_D = 0.

Ф_д = D_1n S – D_2n S +  D_n  _бок

При h  0, S_бок  0, Рис.17

тогда:

D_1n=D_2n

₀₁E₁=₀₂E₂

₁E_1n=₂E_2n

Таким образом при переходе через границу раздела двух диэлектриков тангенциальная составляющая вектора в и нормальная составляющая вектора визменяется непрерывно, а нормальная составляющая вектора и тангенциальная составляющая вектора претерпевают скачек.