3.2 Дивергенция.

Отличие потока от нуля через замкнутую поверхность означает наличие источников или стоков жидкости. Величина Фопределяет суммарную алгебраическую мощность источников в объемV.

-средняя мощность источников.

При V0 — удельная мощность точкиP,ее называютдивергенцией (расхождением) вектора:

Интеграл берется по любой замкнутой поверхности, содержащей точку V.

В декартовых координатах,

Найдем поток через пару граней, перпендикулярных оси X:

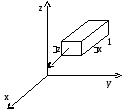
Рис.10

a_n2 = a_x

a_n1 =- a_x

;

3.3 Теорема Остроградского – Гауса

Зная можно найти поток через любую поверхность:

- мощность источников в dV.

Сумма таких выражений, т.е. - суммарная мощность источников в объемеV.

Вследствие не сжимаемости жидкости, суммарная мощность источников равна потоку, вытекающему наружу через S:

;

3.4 Циркуляция

Заморозим мгновенно жидкость во всем объеме, кроме тонкого замкнутого канала по контуру Г. Жидкость будет циркулировать вдоль контураГв одном из двух возможных направлений. В качестве меры такого движения возьмем величину, равную произведению скорости жидкости на длину контура.

Циркуляция поГравна:

(т.к. сечение канала  = const, тоv = const).

В момент затвердевания стенок гасится перпендикулярная стенке составляющая и остаетсяv_l– касательная к контуру.

По закону сохранения импульса сумма начальных импульсов вдоль lравна конечному импульсу жидкости (после установленияv=constв результате соударений элементов жидкости в контуре):

v– скорость циркуляции,v_l – касательная составляющая скорости жидкости в объемеlперед затвердеванием жидкости, тогда:

т.е. для любого

;

Циркуляция обладает свойством аддитивности.

Рис.11

, т.к.

Т.е. циркуляция по контуру Sможет быть представлена как сумма элементарных циркуляцийс по контурам, ограничивающимS.

,

3.5 Ротор

Аддитивность циркуляции позволяет ввести понятие удельной циркуляции, т.е. отношение с к величине поверхностиS.

При конечных размерах Sотношениес/Sдает среднее значение удельной циркуляции.

В точке поле будет характеризовать выражение:

где с– циркуляция вектора по контуруГ,S– площадь контура.

Этого мало, т.к. величина такого предела зависит не только от свойств поля, но и от ориентации контура. В одной и той же точке Рдля разныхбудем получать различные значения. Т.е. это величина ведет себя как проекция некоторого вектора на направление нормали к контуру, по которому берется циркуляция.

Максимальные величины дает модуль вектора, а его направление по , когда максимально.

Этот вектор называется ротором.

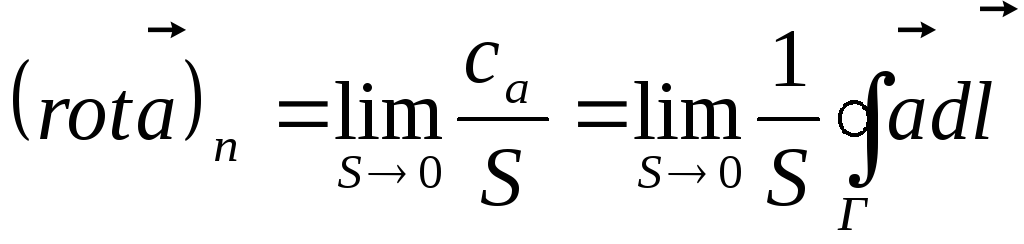
Мы определили проекцию ротора.

В декартовых системах координат нужно найти проекции на оси X, Y, Z.

Найдем

Г– это прямоугольник в плоскостиZOXсо сторонамиyиz. Направление обхода связано сOX– правый винт.

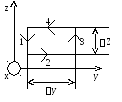
Рис.12

На 1 а_l = -а_z; на 2 а_l = +а_y; на 3 а_l = +а_z; на 4 а_l = -а_y;

с_а= (а_z3 - а_z1) Z - (а_y4 – а_y2) y

где а_zi– среднее значениеа_zна соответствующих участках,а_z3 - а_z1– изменениеа_zсрпри смещении наy, т.е.:

;

Подставив в с_а

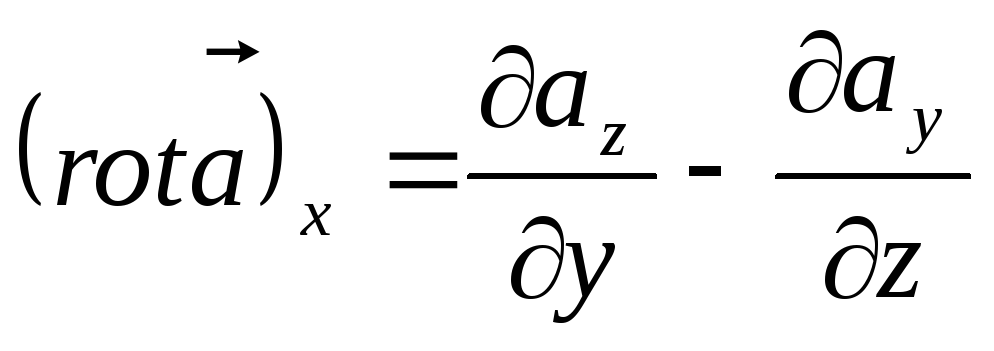
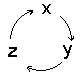Циклическая перестановка
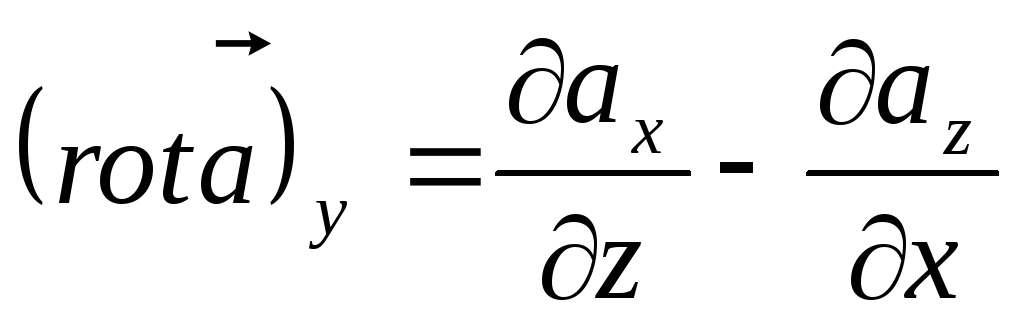
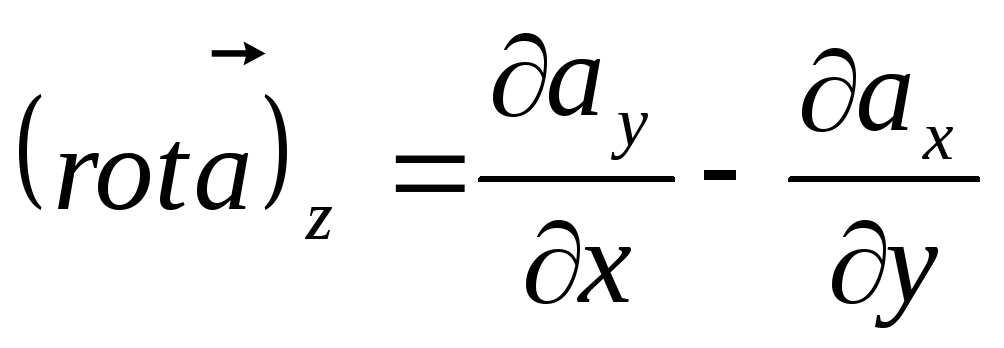