Билет №15.

Задача №1. Найти площадь треугольника, если его стороны соответственно равны ,,.

Д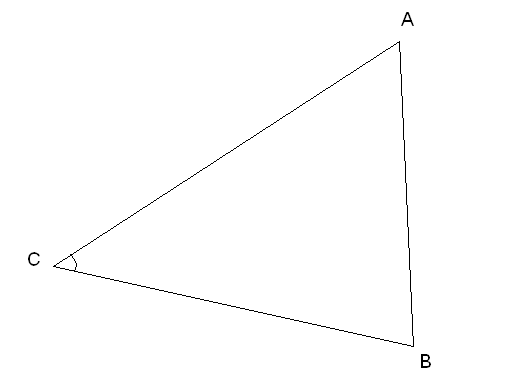ано:,,,

Решение.

AB– большая сторона.

По теореме косинусов:

Ответ:6,5 кв.ед.

З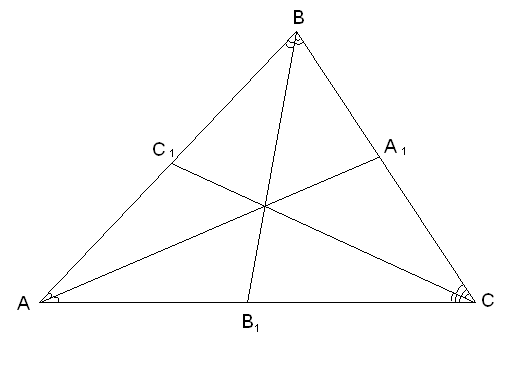адача №2. С помощью теоремы Чевы доказать, что биссектрисы треугольника пересекаются в одной точке.

Дано:,AA₁,BB₁,CC₁– биссектрисы

Доказательство.

По теореме Чевы должно выполняться равенство:

По свойству биссектрисы угла:

;;

Получим:

, значит, биссектрисы пересекаются в одной точке, ч.т.д.

Билет №16.

З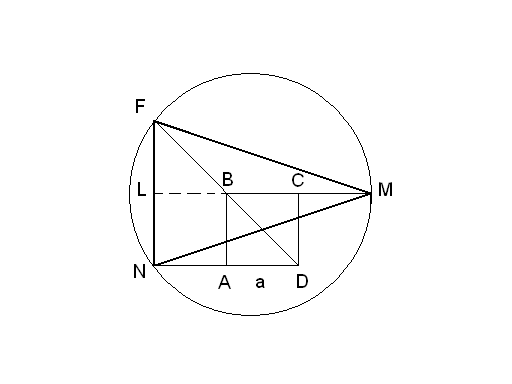адача №1. АВСD – квадрат со стороной а. вершины С, А и В являются серединами отрезков BM, ND и DF соответственно. Найдите радиус окружности, описанной около треугольника NFM.

Дано:ABCD– квадрат,AB=a;

C,A,B– серединыBM,ND,DF

Решение.

- равнобедренный, т.к.

(по построению)

- прямоугольный

Ответ:

Задача №2. Площадь прямоугольника равна 520 м², а отношение его сторон равно 2:5. найти периметр данного прямоугольника.

Дано:ABCD– прямоугольник,м²,.

Решение.

По условию

(м)

Тогда

(м)

Ответ:

Билет №17.

Задача №1. Найдите угол между векторами и, если,,.

Дано:,,.

Решение.

По условию

По условию

Пусть ,, тогда получим систему: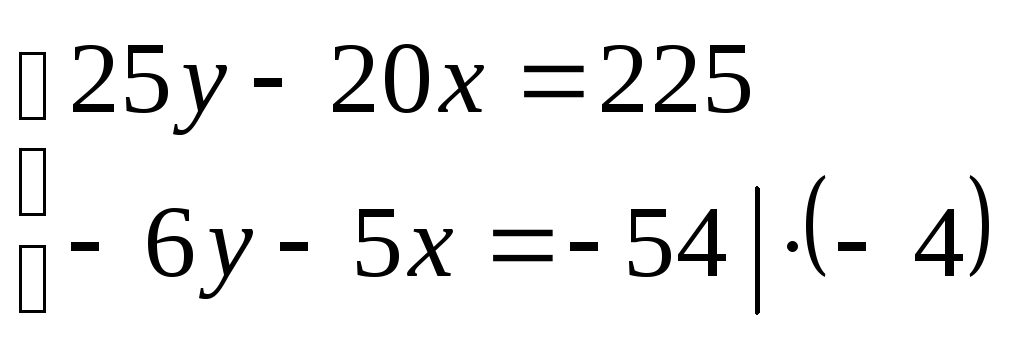

+

, т.е.

,

Итак , значит,

Ответ:

Задача №2. Дано: ,, . вычислите .

Дано:,, .

Решение.

По условию

Получим:

Ответ:

Билет №18.

Задача №1. Постойте отрезок , где а и с – длины данных отрезков.

Дано: отрезкиaиc

Построить:

Построение.

1) На одной стороне произвольного угла от его начала откладываем отрезки cиa;

2) На второй стороне угла откладываем отрезок а;

3) Проводим прямую через концы отрезков с и а и параллельно ей проводим прямую через конец отрезка а;

4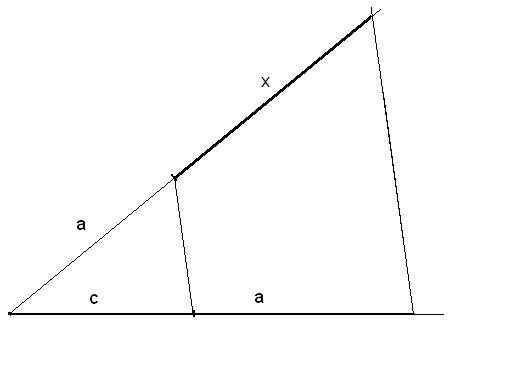) Получившийся отрезок х – искомый (по теореме Фалеса).

З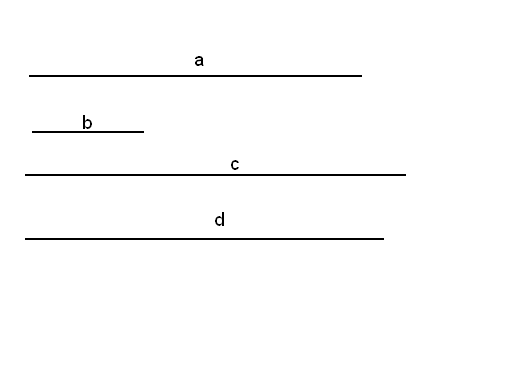адача №2. По данным четырём отрезкам a, b, c, d постройте трапецию с основаниями a и b. При каком соотношении между длинами этих отрезков это невозможно?

Дано: отрезкиa,b,c,d

Построить: трапецию, где

Построение.

1) Построим со сторонамиc,d,a-b

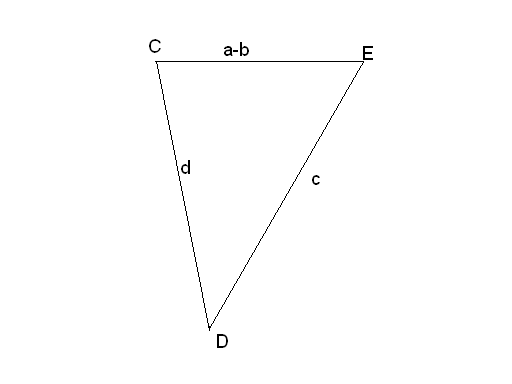
2) Достроим получившийся треугольник до параллелограмма

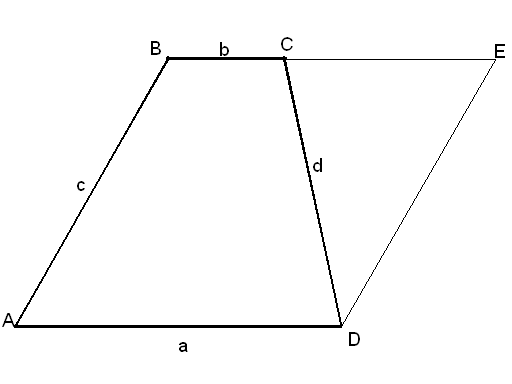
3) оставшаяся часть – искомая трапеция.

Билет №19.

З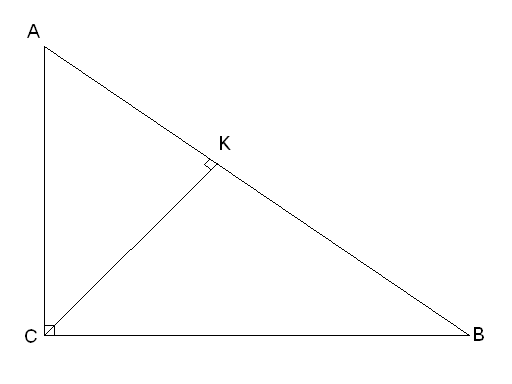адача №1. Найдите острые углы треугольника АВС, если <АВС=90⁰, АС=2, ВК=1, где СК – высота треугольника.

Дано:- прямоугольный,,

,, СК – высота

Решение.

Пусть , тогда по теореме о высоте, опущенной из вершины прямого угла

- не удовлетворяет условию задачи

:

Ответ:,.

Задача №2. В треугольник АВС вписана окружность. С₁, В₁ – точки её касания со сторонами АВ и АС соответственно; АС₁=7, ВС₁=6, В₁С=8. найдите радиусы вписанной и описанной около треугольника АВС окружностей.

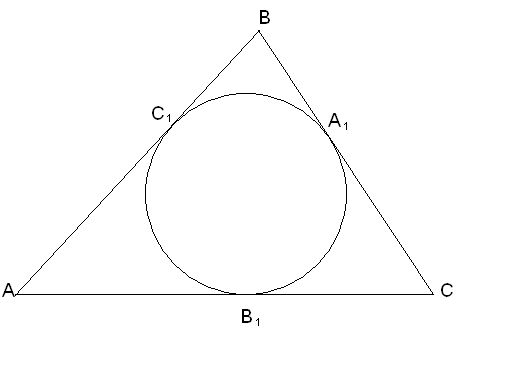
Дано:,,,,и- точки касания Окр

Решение.

,,, как отрезки касательных, выходящих из одной точки.

Тогда ,,,

По формуле Герона: , с другой стороны

Ответ:,