Билет №7.

Задача №1. Доказать, что прямая, проходящая через точку пересечения продолжений боковых сторон трапеции и точку пересечения её диагоналей, делит пополам основания трапеции.

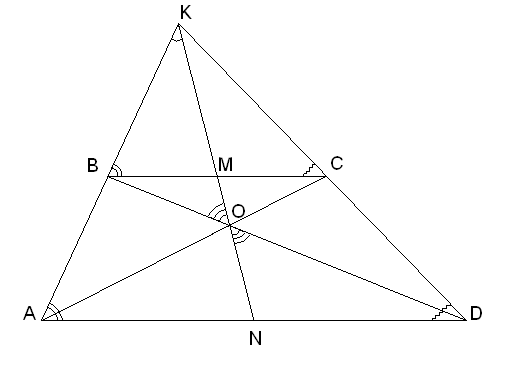
Дано:ABCD– трапеция,

Доказательство. I способ.

Пусть К – точка пересечения боковых сторон трапеции. Обозначим через М и Nсередины основанийBCиADсоответственно.

и

Т.к. любая прямая, проходящая через точку К, делит основания трапеции в одном и том же отношении (считая от вершины А или В соответственно). Отсюда следует, что точки К, M,Nлежат на одной прямой.

Точно также всякая прямая, проходящая через М делит ADиBCв одном и том же отношении (считая от А или В), значит, точкиM,O,Nтоже находятся на одной прямой.

Таким образом, все четыре точки M,N,O,Kлежат на одной прямой, ч.т.д.

IIспособ.

Проведем прямую KN(N– серединаAD), докажем, что.

ипо двум углам (- общий,,)

, т.к.M– серединаBC.

Проведем прямую ON

, как накрест лежащие углы)

,ч.т.д.

IIIспособ.

Из теоремы Чевы для и точки О:

, тогда

По теореме Фалеса:

ипо двум углам (- общий,,)

, ч.т.д.

Задача №2. Найдите площадь трапеции с боковыми сторонами 13 и 20 и основаниями 6 и 27.

Д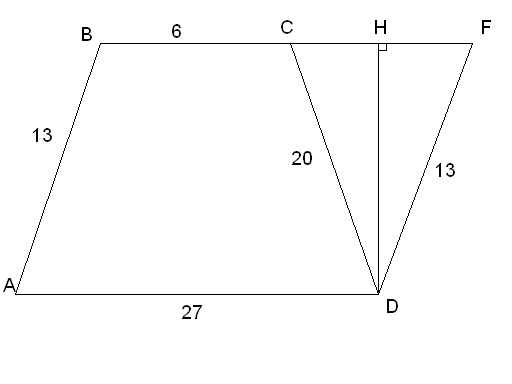ано:ABCD– трапеция,

BC=6,AB=13,CD=20,AD=27

Решение. I способ.

Достроим трапецию до параллелограмма ABFD, тогдаи(по свойству параллелограмма)

По формуле Герона:

Но с другой стороны

Ответ:кв.ед.

I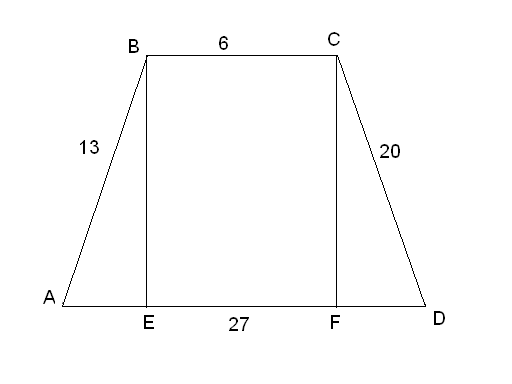I способ.

Заметим, что в трапецию можно вписать окружностьвысота трапеции равна двум радиусам.

- прямоугольный. По теореме Пифагора:

Ответ:кв.ед.

Билет №8.

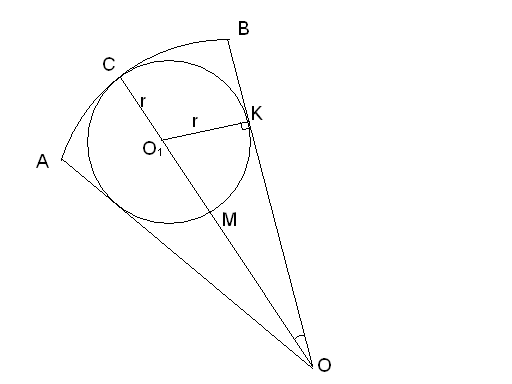Задача №1. В круговой сектор с углом 60⁰ помещён круг, касающийся дуги сектора и обоих радиусов. Найдите отношение площади сектора и площади круга.

Дано:AOB– круговой сектор,,

Окр.(О₁;r)

Решение.

Тогда

- прямоугольный,, тогда, а.

По теореме о квадрате касательной

Тогда

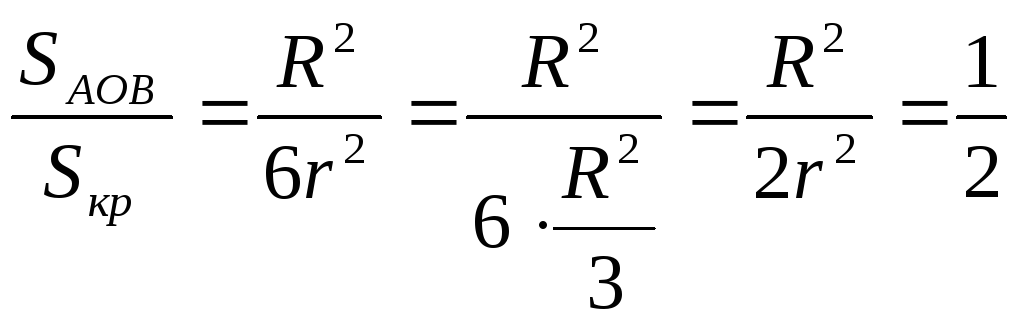
Ответ:

З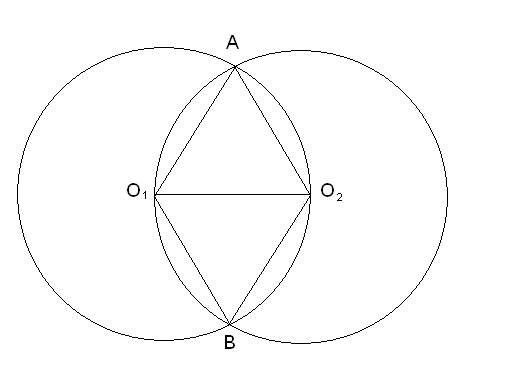адача №2. Найдите площадь фигуры и длину границ фигуры, являющейся общей частью двух кругов радиуса R каждый, если расстояние между их центрами также равно R.

Дано:,,

Решение.

- равнобедренный

,

, тогда

Длина границы

Ответ:,

Билет №9.

Задача №1. Доказать, что площадь прямоугольной трапеции, в которую можно вписать окружность, равна произведению её оснований.

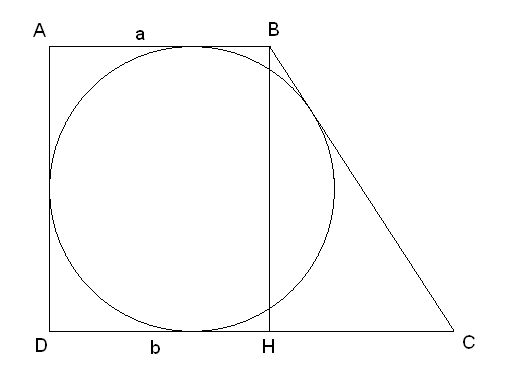
Дано:ABCD– вписанная трапеция; а,b– основания

Доказательство.

1) Дополнительное построение:

В

2) ABCD– описанная

3)

4) - в силу, ч.т.д.

З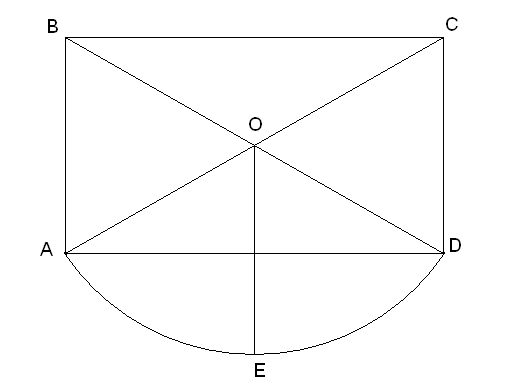адача №2. Радиус окружности, описанной около прямоугольника, равен 5 см. Одна из его сторон равна 6 см. Найти: а) площадь прямоугольника; б) угол между диагоналями прямоугольника.

Дано:ABCD– прямоугольник,OE=5 см,AB=6 см,

Окр.(O;R) - описанная

Решение.

А) Т.к. Окр.(O;R) – описанная, то О- точка пересечения диагоналей прямоугольника, ОD=R

(см)

(см²)

Б) : по теореме косинусов

Ответ:(см²),.

Билет №10.

З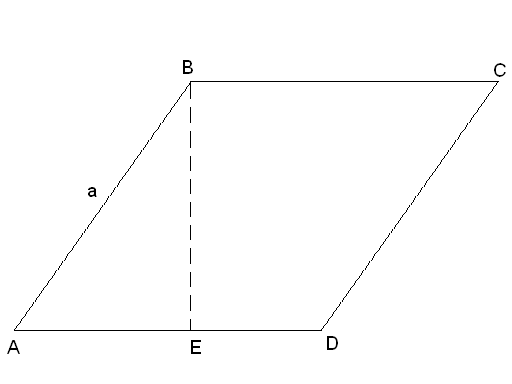адача №1. Высота ромба, проведённая из вершины его тупого угла, делит сторону ромба в отношении 1:2, считая от вершины его острого угла. Какую часть площади ромба составляет площадь вписанного в него круга?

Дано:ABCD– ромб,BE– высота,

Решение.

1)

2)

3)

4)

Ответ:

Задача №2. Составить уравнение окружности с центром на прямой у=4 и касающейся оси абсцисс в точке (3; 0). Найти координаты точки пересечения окружности с прямой у=х.

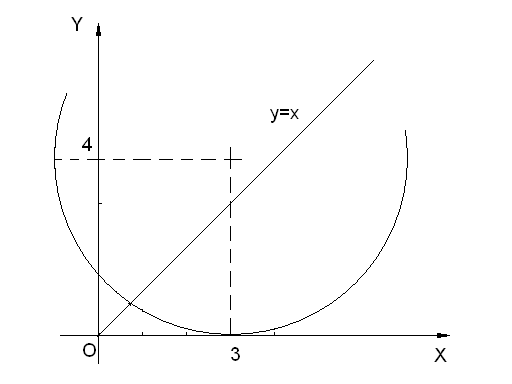
Решение.

А) Уравнение окружности имеет вид , где- центр окружности,r– ее радиус.

Т.к. О₀лежит на прямойи касается оси абсцисс в точке, то

- уравнение окружности

Б) - биссектрисаIиIIIкоординатных углов

Т.к. , то

Ответ:.