
- •2008Г. Тезисы к работе: «Решебник к задачам экзаменационных билетов по геометрии для классов с углубленным изучением математики за курс основной средней школы».
- •Билет №1.
- •Билет №2.
- •Билет №3.
- •Билет №4.
- •Билет №5.
- •Билет №6.
- •Билет №7.
- •Билет №8.
- •Билет №9.
- •Билет №10.
- •Билет №11.
- •Билет №12.
- •Билет №14.
- •X – искомый отрезок
- •Билет №15.
- •Билет №16.
- •Билет №17.
- •Билет №18.
- •Билет №19.
- •Билет №20.
- •Билет №21.
- •Билет №22.
- •Билет №23.
- •Билет №24.
- •2008Г. Тезисы к работе Мельниченко Анны: «Решебник к задачам экзаменационных билетов по геометрии для классов с углубленным изучением математики за курс основной средней школы».
Билет №11.
Задача №1. Центр описанной около треугольника окружности симметричен центру вписанной окружности относительно одной из сторон треугольника. Найти углы этого треугольника.
Д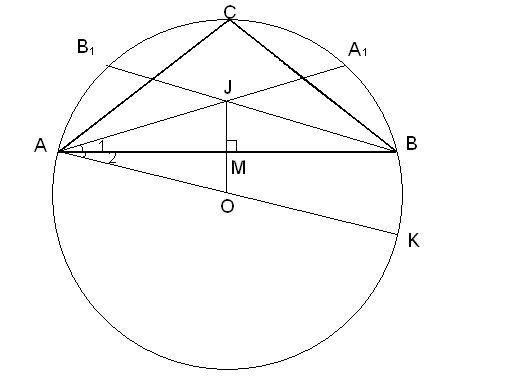 ано:
ано:![]() ,
окр.(О;R) – описанная,
окр.(J;r) –
вписанная.
,
окр.(О;R) – описанная,
окр.(J;r) –
вписанная.
Решение.
Т.к. цетры вписанной и описанной
окружностей симметричны относительно
стороны треугольника, то центр описанной
окружности лежит вне
![]() - тупоугольный
- тупоугольный
Заметим: J– центр вписанной
окружности и О – центр описанной
окружности лежат на диаметре. Т.к. диаметр
перпендикулярен хорде, то![]() - медиана
- медиана![]() и
и![]() ,
значит,
,
значит,![]() - равнобедренный.
- равнобедренный.
Дополнительные построения:
![]() - биссектрисы
- биссектрисы![]() и
и![]()
![]() .
.
Дополнительное построение:
![]() .
.
![]() =
=![]() (
(![]() ,
т.к.JиO–
симметричны относительно М,
,
т.к.JиO–
симметричны относительно М,![]() -
общая). Значит
-
общая). Значит![]() .
.
AK– диаметр, т.к. проходит
через центр окружности![]() ,
,
![]()
Ответ:![]() .
.
З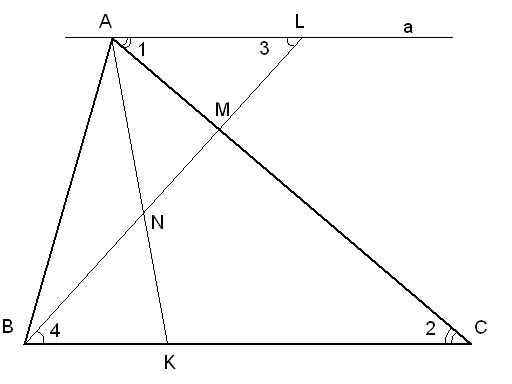 адача
№2.
В треугольнике АВС на стороне АС взята
точка М такая, что АМ=
адача
№2.
В треугольнике АВС на стороне АС взята
точка М такая, что АМ=![]() АС,
а на стороне ВС – точка К такая, что
ВК=
АС,
а на стороне ВС – точка К такая, что
ВК=![]() .
В каком отношении отрезок ВМ делит
отрезок АК?
.
В каком отношении отрезок ВМ делит
отрезок АК?
Дано:![]() ,
,![]() ,
АМ=
,
АМ=![]() АС,
АС,![]() ,
ВК=
,
ВК=![]() .
.
Решение.
1) Проведем через вершину А прямую,
параллельную BC.![]()
Пусть
![]()
2)
![]() (т.к.
(т.к.![]() )
)
![]()
3)
![]() (по двум углам), тогда
(по двум углам), тогда![]()
Ответ:![]()
Билет №12.
Задача №1. Длины диагоналей ромба пропорциональны числам 3 и 4, его сторона равна 20 см. Найти: а) длины диагоналей; б) радиус окружности, вписанной в ромб.
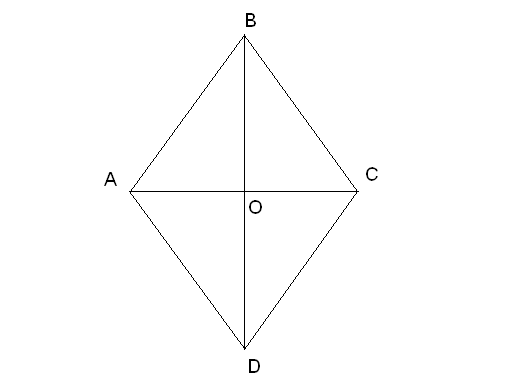
Дано:ABCD– ромб,![]() ,
,![]()
Решение.
А) ABCD– ромб, значит![]() и
и![]()
![]()
![]()
![]() ,
т.е.
,
т.е.
![]()
![]()
![]() см
см
![]() см
см
![]() см,
тогда
см,
тогда![]() см
см
Б) ABCD– описанный![]()
![]() (см2)
(см2)
![]() (см)
(см)
Ответ:![]() ;
;![]() см
см
З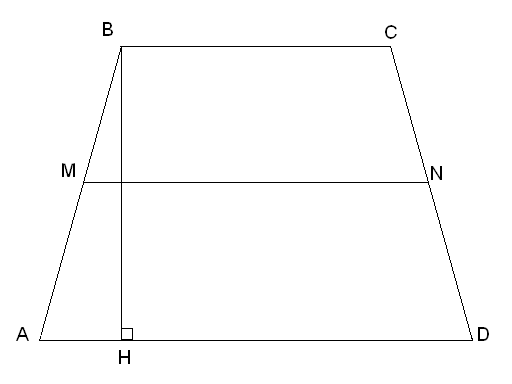 адача
№2.
Найти площадь равнобедренной трапеции,
у которой основания равны 8 и 18 см, а
боковая сторона равна средней линии.
адача
№2.
Найти площадь равнобедренной трапеции,
у которой основания равны 8 и 18 см, а
боковая сторона равна средней линии.
Дано:ABCD– равнобедренная трапеция,
![]() см,
см
см,
см![]() ,MN– средняя линия,
,MN– средняя линия,![]()
Решение.
Т.к. MN– средняя линия, то![]()
Т.к. ABCD– равнобедренная,
то![]() (см)
(см)
![]() :
по теореме Пифагора:
:
по теореме Пифагора:![]() (см)
(см)
![]() (см2)
(см2)
Ответ:![]() (см2)
(см2)
Билет №13.
Задача №1. В равнобедренном треугольнике АВС АС=b, AB=BC=a, AN и СМ – биссектрисы углов А и С. Найти длину отрезка MN.
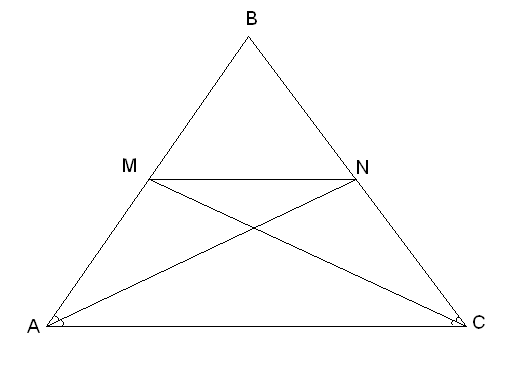
Дано:![]() ,
,![]() ,
,![]() ,ANиMC–
биссектрисы
,ANиMC–
биссектрисы![]() и
и![]()
Решение.
1) Пусть
![]() ,
тогда
,
тогда![]()
CM– биссектриса![]() ,
откуда
,
откуда![]()
![]()
2) С другой стороны
![]() (
(![]() - общий,
- общий,![]() )
)
![]()
![]()
Ответ:![]()
Задача №2. Гипотенуза прямоугольного треугольника делится на отрезки 5 см и 12 см точкой касания этого треугольника со вписанной в него окружностью. На какие отрезки делит катет треугольника биссектриса его меньшего угла?
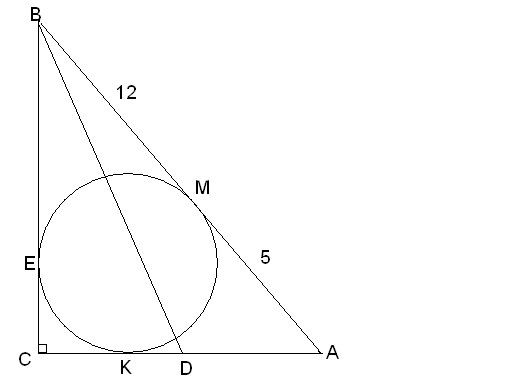
Дано:![]() - прямоугольный,BK–
биссектриса, окр.(О;r),
- прямоугольный,BK–
биссектриса, окр.(О;r),
E,K,M– точки касания,![]() см,
см,![]() см
см
Решение.
Пусть
![]() ,
тогда
,
тогда![]() ,
,![]() ,
,![]()
По теореме Пифагора:
![]()
![]()
![]()
![]()
![]()
![]() - не удовлетворяет условию
- не удовлетворяет условию
Итак,
![]() см,
см,![]() см.
см.
По свойству биссектрисы угла:
![]()
Ответ:![]()
Билет №14.
З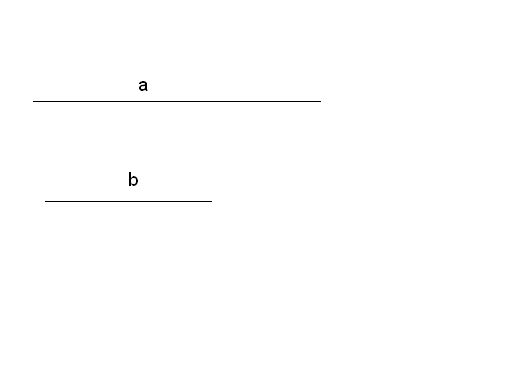 адача
№1.
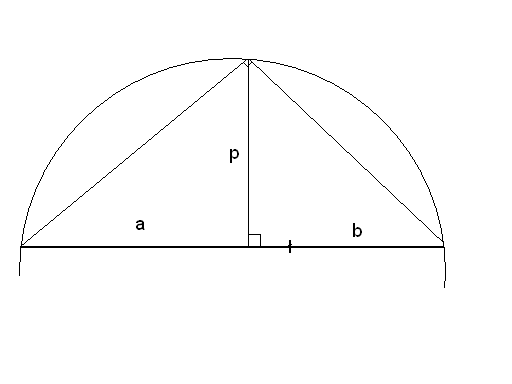
Постройте отрезок длины
адача
№1.
Постройте отрезок длины![]() ,
гдеa
>b,
если a
и b
– длины двух отрезков.
,
гдеa
>b,
если a
и b
– длины двух отрезков.
Дано: отрезкиaиb
П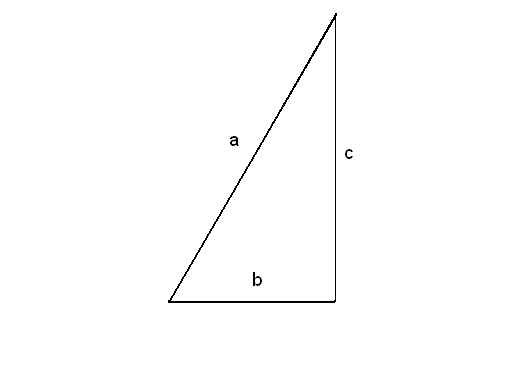 остроение.
остроение.
1)
![]()
2)
![]()
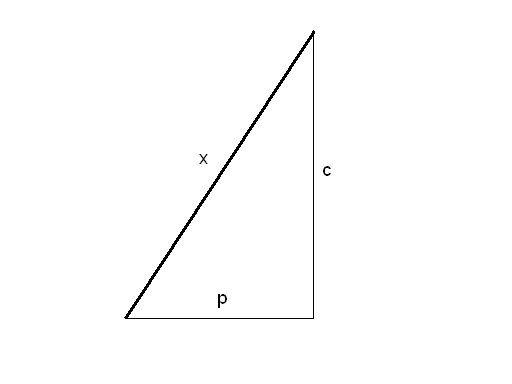
3)
![]()
X – искомый отрезок
З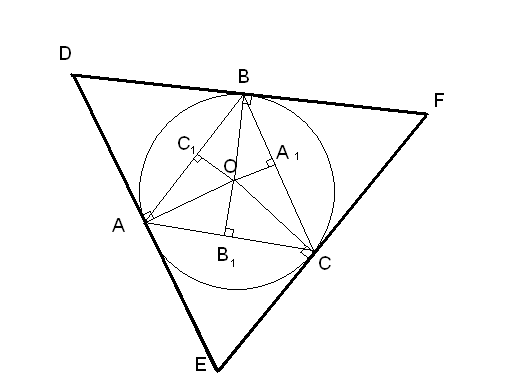 адача
№2.
Постройте треугольник по трём точкам
касания его сторон с вписанной в
треугольник окружностью.
адача
№2.
Постройте треугольник по трём точкам
касания его сторон с вписанной в
треугольник окружностью.
Дано: точкиA,B,C.
Построить:![]() ,
гдеA,B,C–
,
гдеA,B,C–
точки касания сторон с вписанной окружностью.
Построение:
1) Соединим точки A,B,C
2) OA1,OB1,OC1– серединные
перпендикуляры для
![]()
3) Построим окружность с центром
в точке О и радиусом OA
4) Строим EF,DE,DF, перпендикулярные
радиусам окружности
5)
![]() - искомый
- искомый
