МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Решебник к задачам

экзаменационных билетов

по геометрии для классов

с углубленным изучением

математики за курс

основной средней школы

Автор: Будлянская

Наталья Леонидовна

Должность: учитель математики.

Адрес автора: Хабаровский край

г. Комсомольск – на – Амуре

ул. Вокзальная д.72 кв. 71

т. (4217)599503.

Адрес образовательного учреждения: Хабаровский край

г. Комсомольск – на – Амуре

ул. Пирогова 21

т. (4217)598260.

г. Комсомольск - на - Амуре

2008Г. Тезисы к работе: «Решебник к задачам экзаменационных билетов по геометрии для классов с углубленным изучением математики за курс основной средней школы».

Экзамены в 9 классе – это очень важный этап в жизни каждого школьника. Для кого-то это первая в жизни настоящая проверка знаний, для кого-то способ оценить свои силы перед экзаменом в 11 классе. Тем не менее, экзамены – это всегда волнение и долгие дни подготовки.

Чтобы облегчить подготовку к экзамену по геометрии, я создала такой решебник. В него входят задачи, предлагаемые на экзамене и решения к ним. Без серьезных знаний по предмету и при отсутствии «опыта» в решении таких задач, на экзамене многие ученики испытывают большие трудности. Поэтому мне показалось, что и учащимся, и учителям будет полезен мой решебник. Многие задачи решены двумя и даже тремя способами, все подробно объяснены и иллюстрированы.

Даже если с будущего года экзамен по геометрии за 9 классов будет проходить в форме ЕГЭ, мне кажется, что мой сборник будет полезен и интересен учащимся математических классов и учителям.

Билет №1.

Задача №1. Сумма сторон треугольника равна 8, а два из его углов равны соответственно 30° и 45°. Найти все возможные значения периметра.

Решение. Возможны три случая взаимного расположения известных элементов треугольника:

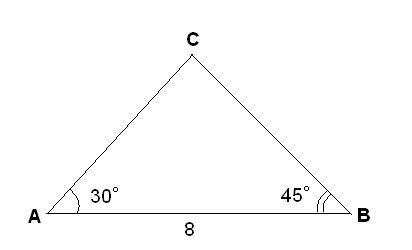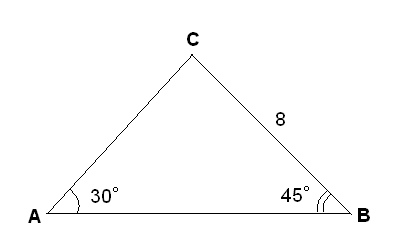А)Б)В)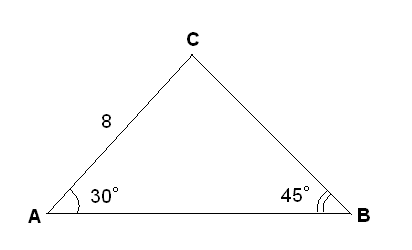

А) По теореме о сумме углов треугольника , АС=8;

Sin105°=Sin (90°+15°) =Cos15°0, 9659

;

P

Б) По теореме о сумме углов треугольника , ВС=8;

;

P

В) По теореме о сумме углов треугольника , АВ=8;

;

P

Ответ:;;

Задача №2. Построить треугольник по данным двум углам и биссектрисе при вершине третьего угла.

Дано:

Построение:

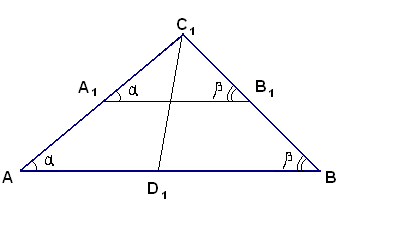1. Построим произвольный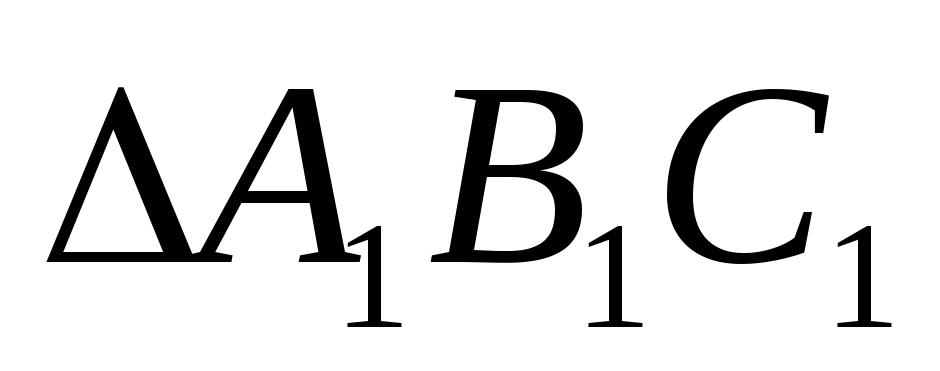подобный искомому, взяв произвольный отрезок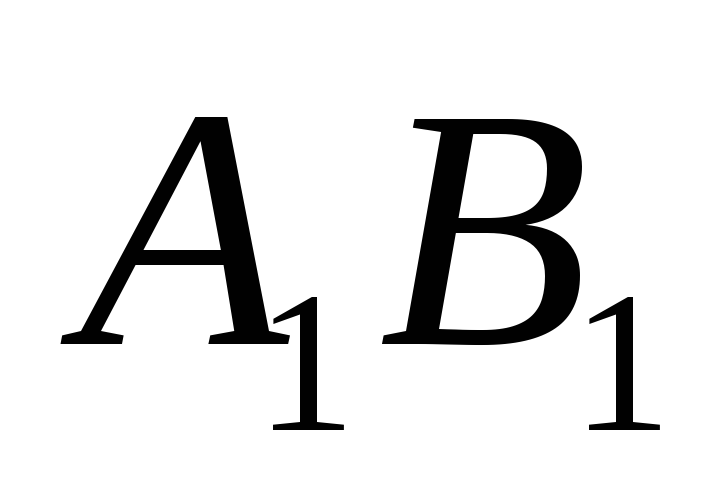и отложив углыи.

2. Построим биссектрису .

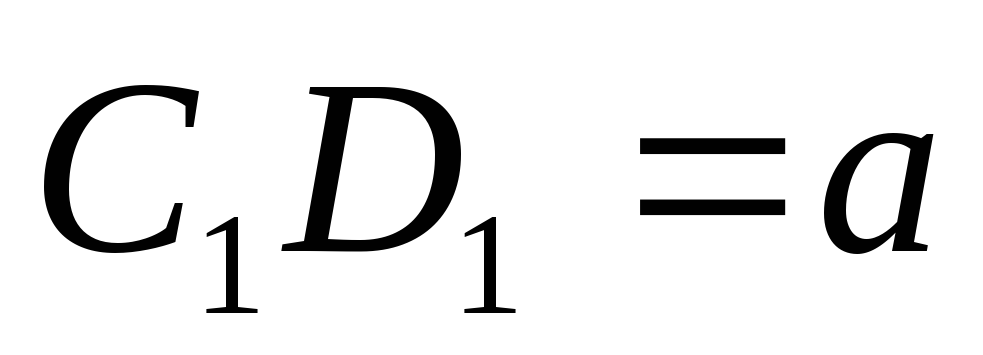3. Проведем через 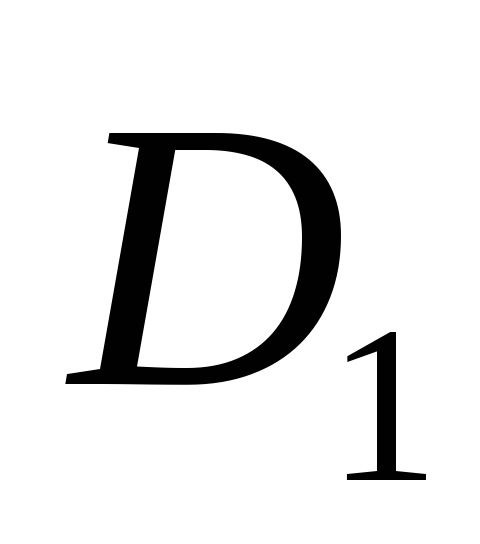прямую параллельную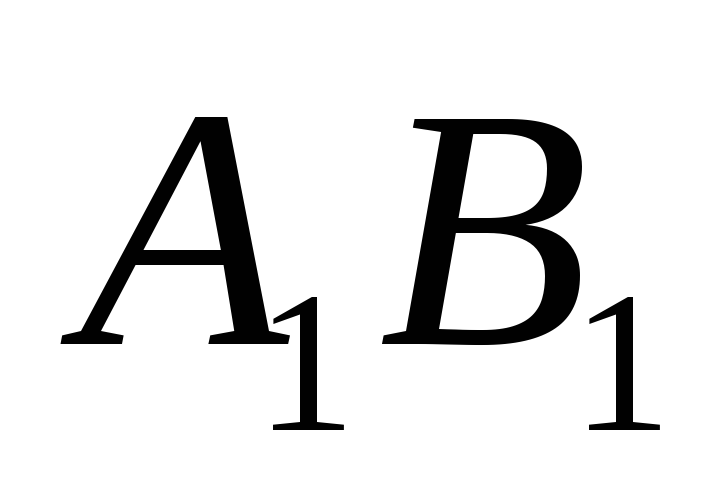до пересечения с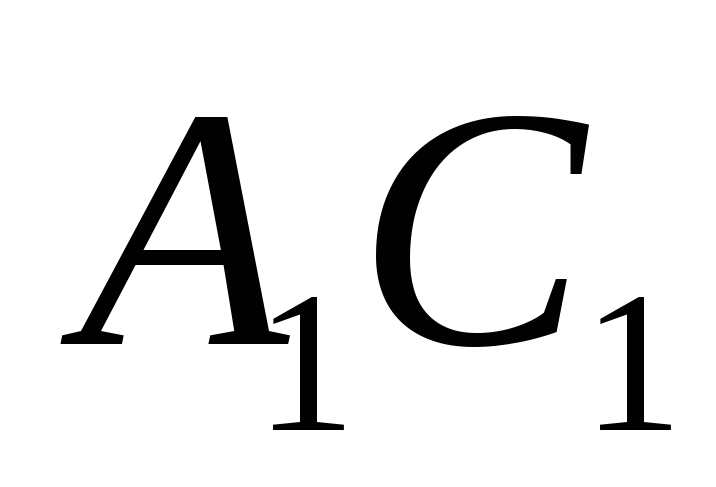и.

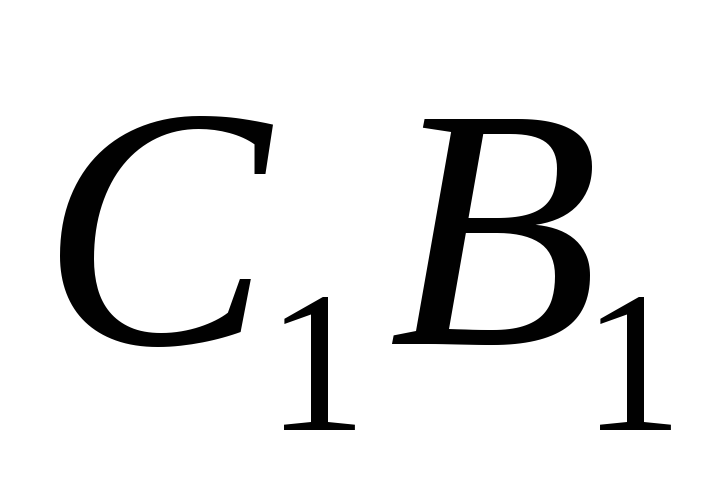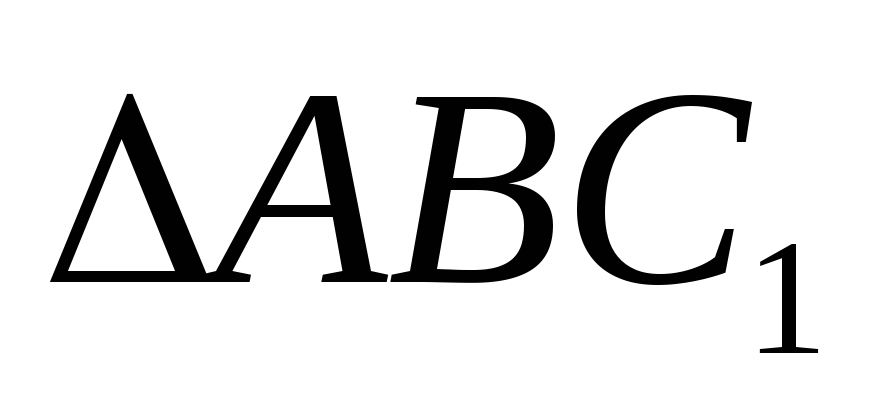4. - искомый.

Билет №2.

З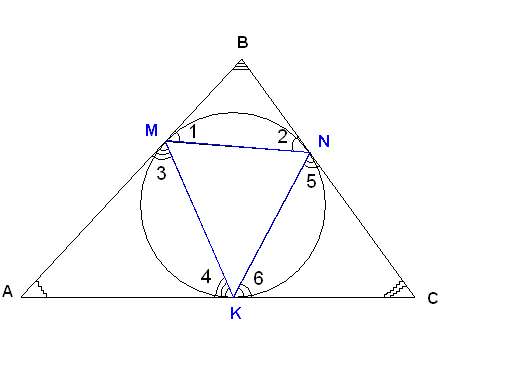адача №1. В треугольнике АВС углы А и В равны 38⁰ и 86⁰ соответственно. Найдите углы треугольника, вершинами которого являются точки касания сторон с вписанной в АВС окружностью.

Дано:,

Решение.

По свойству касательных: ,,, т.е.- равнобедренные.

.

Тогда ;

;

.

Ответ:,,.

З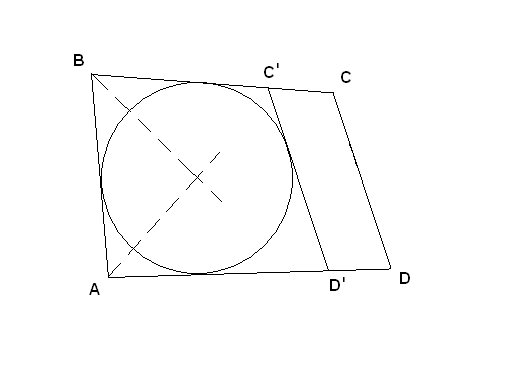адача №2. Доказать, что если в выпуклом четырёхугольнике противоположные стороны равны, то в этот четырёхугольник можно вписать окружность.

Дано:

Доказательство.

Точка пересечения биссектрис углов АиВ равноудалена от сторонAD, AB и BC, поэтому можно провести окружность с центром в точкеО, касающуюся указанных трех сторон. Докажем, что эта окружность касается также стороныCDи , значит, является вписанной в четырехугольникABCD.

Предположим, что окружность вписать нельзя. Проведем биссектрисы и, точка пересеченияО– центр окружности, касающейсяAD, AB, BC. Тогда CD либо секущая для окружности, либо находится вне ее. Рассмотрим второй случай.

Проведем касательную к окружности.. Т.к.- описанный, то, по свойству описанного четырехугольника.

Но подставим в

равенство (2)

, ноиз равенства (1)

- чего быть не может в четырехугольнике. Предположение не верно.

*Аналогично рассматривается случай, когда CD– секущая.

Вывод: в данный четырехугольник можно вписать окружность, ч.т.д.