
3.3. Скалярное, векторное, смешанное произведение векторов
Определение 3. 6.
Число,
равное произведению длин двух векторов
на косинус угла между ними называется
скалярным
произведением этих векторов. Для векторов
![]() и
и![]() их скалярное произведение обозначается
(
их скалярное произведение обозначается
(![]() ,
,![]() ),
или
),
или ![]() .
.![]() .
.
Таким образом, по определению
![]() .
.![]() = |
= |![]() |.|
|.|![]() |
cos
|
cos![]() .
.
Скалярное произведение обладает свойствами:
 .
.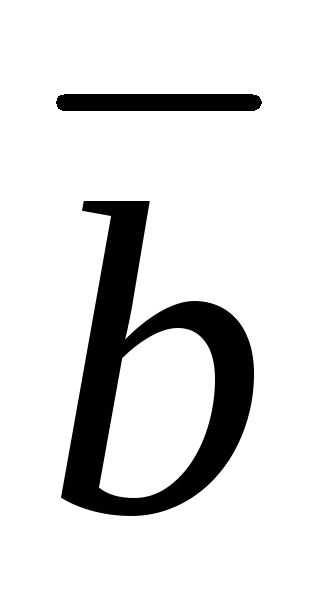 =
=
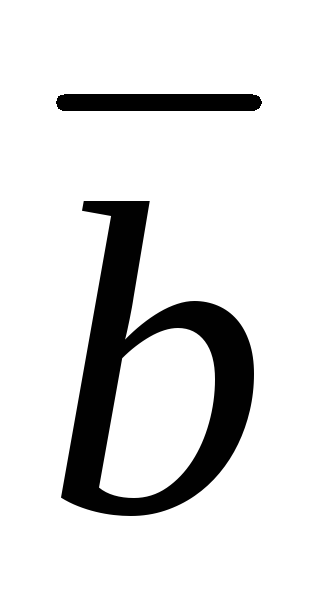 .
. ;
; .(
.(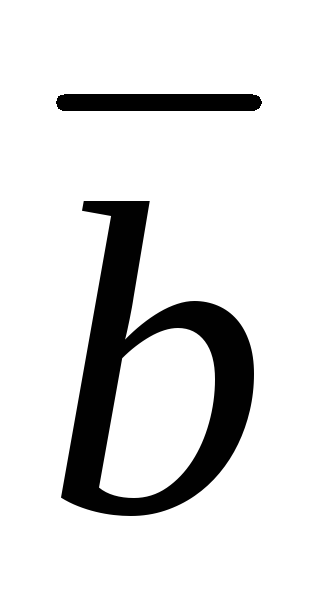 +с)
=
+с)
=  .
.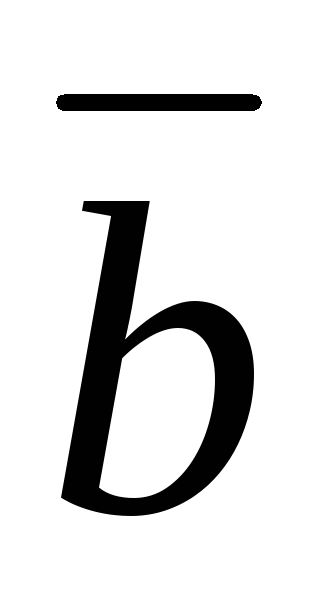 +
+
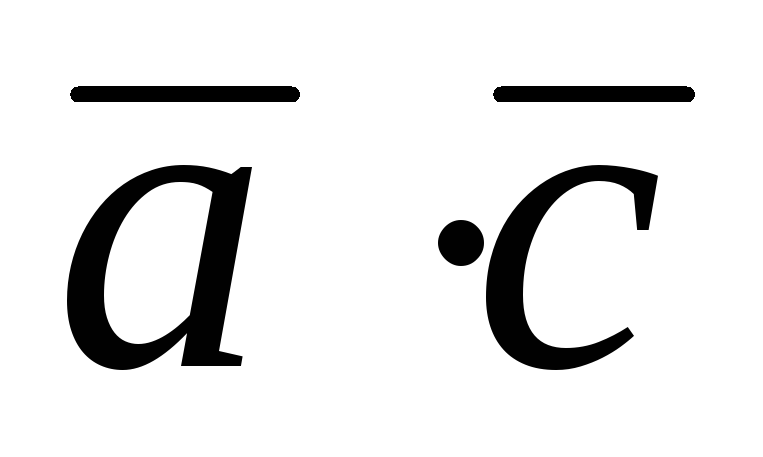 ;
; .
. = |
= | |2
=
|2
=  2
– скалярный квадрат; отсюда
2
– скалярный квадрат; отсюда
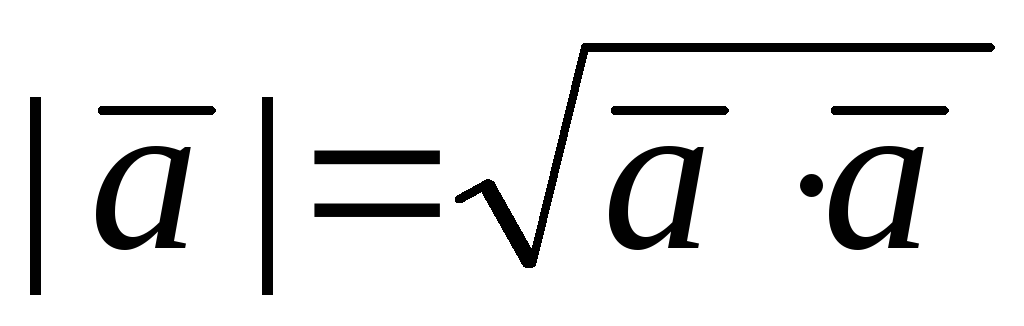 ;
;
 .
.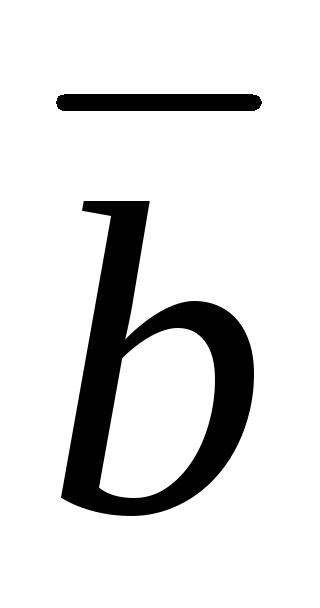 = (
= ( ).
).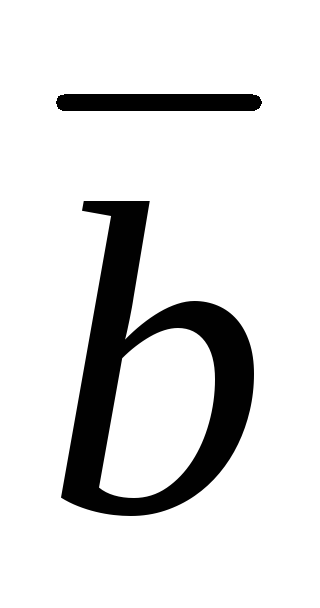 =
=  .(
.( );
); .
.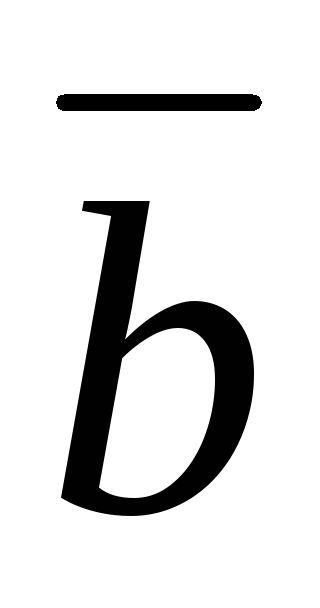 =
0 тогда и только тогда, когда хотя бы
один из векторов нулевой, либо когда
векторы
=
0 тогда и только тогда, когда хотя бы
один из векторов нулевой, либо когда
векторы  и
и
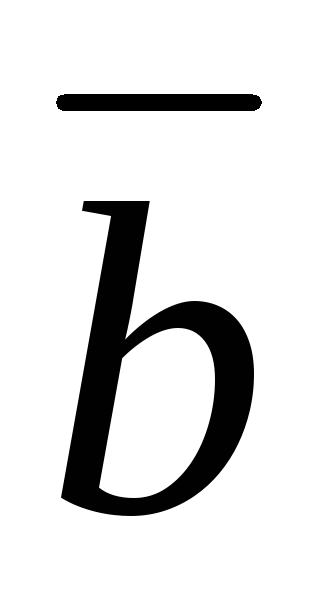 ортогональны;
ортогональны;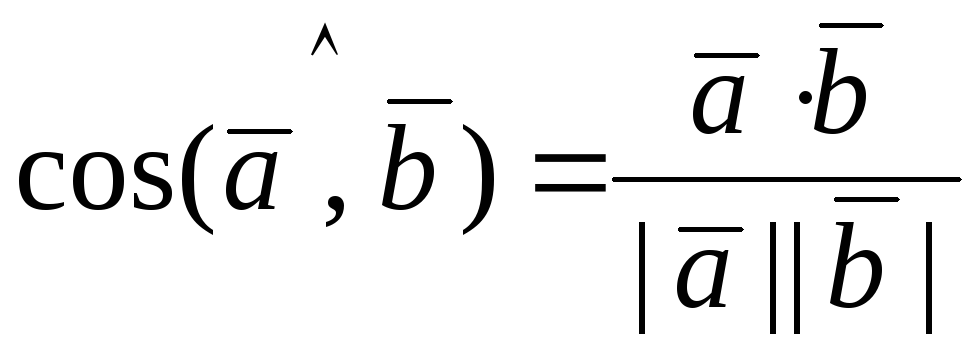 .
Пользуясь этим свойством, получим
.
Пользуясь этим свойством, получим
![]() .
.
Заметим, что для ортонормированного базиса {i,j,k } пространства V3 справедливы следующие соотношения
![]() ,
,
![]() .
.
Пусть в ДПСК, порожденной репером [O,i,j,k], заданы два вектора
![]() и
и ![]() .
.
Используя перечисленные свойства скалярного произведения, получим для этих векторов:
![]() .
.![]() =
=
![]() .
.![]() =
=
![]()
+
![]() =
=
=
![]() .
.
Таким образом, если векторы заданы своими координатами в ДПСК, то их скалярное произведение равно сумме произведений соответствующих координат этих векторов:
![]() .
.![]() =
=
![]() .
.
Пользуясь этим правилом, можно записать в координатной форме
|![]() |
= (
|
= (![]() .
.![]() )
=
)
=
![]() ,
,
![]() =
=
![]() .
.
Учитывая эти формулы и следствие из свойства 6, находим:
![]()
![]()
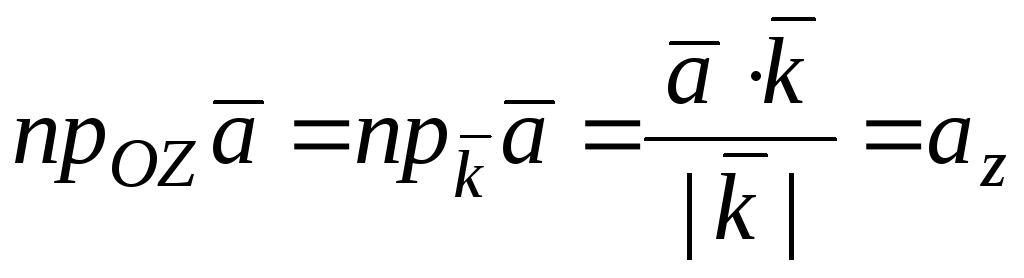 ,
,
т.е. в ДПСК координаты вектора равны его проекциям на соответствующие оси координат.
Для направляющих косинусов вектора а имеем
![]() ,
,
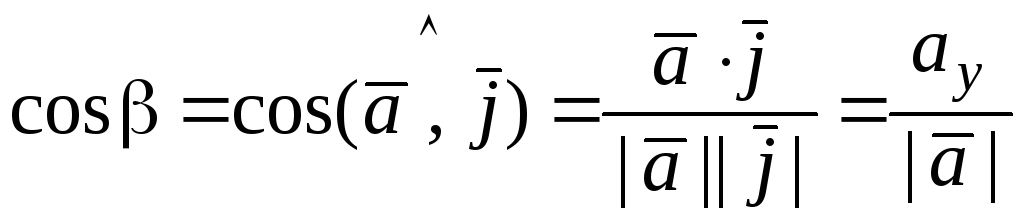 ,
,
![]() .
.
Рассмотрим орт ао вектора а. Учитывая координаты вектора а,находим
ао
=
![]() .
.
Следовательно, направляющие косинусы вектора равны координатам его орта и наоборот, т.е. можно записать ао = (cos, cos, cos).
Определение 3.7.
Упорядоченная тройка векторов а,b,c , совмещенных началами, называется правой тройкой, если из конца третьего векторас кратчайший поворот от первого вектораа ко второму векторуb виден осуществляющимся против часовой стрелки.
В противном случае тройка векторов называется левой. На рис.7а изображена правая тройка векторов, а на рис.7б – левая.


б)
Рис.7
а)
ДПСК, которой мы договорились пользоваться, строится на основе правой тройки (i,j,k).
Определение 3.8.
Векторным произведением векторов а и b называется векторv , удовлетворяющий свойствам:
а) |![]() |=
|
|=
|![]() |.|
|.|![]() |.sin
|.sin![]() ,
,
б)
векторv
перпендикулярен плоскости, в которой
лежат векторы ![]() и
и
![]() ;
;
в) векторы
![]() ,
,
![]() ,v,
взятые в указанном порядке, образуют
правую тройку
,v,
взятые в указанном порядке, образуют
правую тройку
Векторное
произведение обозначается ![]()
![]() или [
или [![]() ,
,
![]() ].
Векторное произведение обладает
свойствами:
].
Векторное произведение обладает
свойствами:
1) ![]() ,
,
2) ![]() ,
,
3) ![]() =
(
=
(![]() )
=
)
= ![]() ,
,
4) ![]() =0
(
=0
(![]() 0,
0,
![]() 0)
тогда и только тогда, когда векторы
0)
тогда и только тогда, когда векторы ![]() и
и
![]() коллинеарны. В частности,
коллинеарны. В частности,
![]() .
.
Для базисных векторов `i,`j,`k имеют место соотношения:
![]()
![]()
![]() .
.
Пусть векторы заданы своими координатами:
![]() и
и ![]() .
.
Используя перечисленные свойства, получим
![]() =
=
![]()
![]() =
=
![]()
+ ![]() =
=
=
![]()
=
![]()
= .
.
Таким образом, через координаты перемножаемых векторов a = (ax, ay, az) и b = (bx, by, bz) векторное произведение может быть записано в виде символического определителя
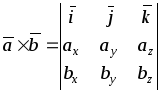 .
.
или в виде координатной строки
![]()
![]() =
=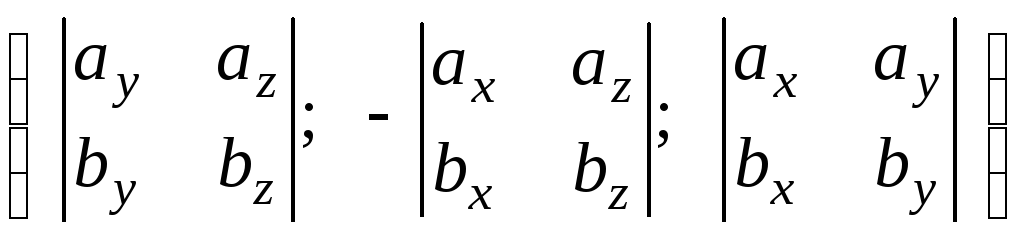 .
.
Р ассмотрим
параллелограмм ABCD,
построенный на вектораха
иb
как на сторонах (рис. 8). Площадь этого
параллелограмма равна
ассмотрим
параллелограмм ABCD,
построенный на вектораха
иb
как на сторонах (рис. 8). Площадь этого
параллелограмма равна
Sпар.
= |AB|.|AD|.sin
= |![]() |.|
|.|![]() |.sin
= |
|.sin
= |![]()
![]() |.
|.
Таким образом, с геометрической точки зрения, модуль векторного произведения двух неколлинеарных векторов численно равен площади параллелограмма, построенного на этих векторах как на сторонах.
Определение 3.9.
Смешанным
произведением векторова,b,с
называется скалярное произведение
вектора ![]()
![]() на вектор с.
Обозначается смешанное произведение
на вектор с.
Обозначается смешанное произведение
![]() .
.![]() .
.![]() или
или ![]()
![]()
![]() .
.
Таким образом, по определению, смешанное произведение трех векторов – это число, равное
![]() .
.![]() .
.![]() =
(
=
(![]()
![]() ,с).
,с).
Свойства смешанного произведения:
1) ![]() .
.![]() .
.![]() =
=
![]() .
.![]() .
.![]() =
= ![]() .
.![]() .
.![]() ,
т.е. при циклической перестановке
множителей смешанное произведение не
меняется;
,
т.е. при циклической перестановке
множителей смешанное произведение не
меняется;
2) ![]() .
.![]() .
.![]() = –
= –
![]() .
.![]() .
.![]() = –
= –![]() .
.![]() .
.![]() = –
= –![]() .
.![]() .
.![]() ,
т.е. смешанное произведение меняет знак
при перестановке соседних множителей;
,
т.е. смешанное произведение меняет знак
при перестановке соседних множителей;
3) ![]() .
.![]() .
.![]() = 0 (
= 0 (![]() 0,
0,
![]() 0,
0,
![]() 0)
тогда и только тогда, когда векторы
a,b,c
компланарны.
0)
тогда и только тогда, когда векторы
a,b,c
компланарны.
Если векторы a,b,c заданы своими координатами: a = ( аx , ay , az), b = (bx , by , bz), с = ( сx , сy , сz),
то, используя координатную форму скалярного и векторного произведений, получим
![]() .
.![]() .
.![]() =
(
=
(![]()
![]() ,с)
=
,с)
= 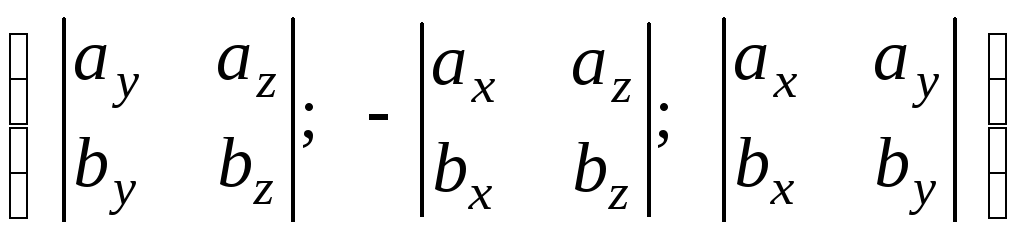 .(
сx
, сy
, сz)
=
.(
сx
, сy
, сz)
=
=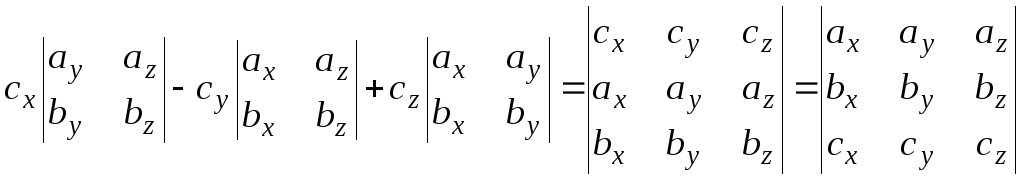
Следовательно, в координатной форме смешанное произведение имеет вид
![]() .
.![]() .
.![]() =
= 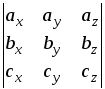 .
.
Р ассмотрим
геометрическую интерпретацию смешанного
произведения. Построим на вектораха,b,с
как на ребрах параллелепипед (рис.9).
ассмотрим
геометрическую интерпретацию смешанного
произведения. Построим на вектораха,b,с
как на ребрах параллелепипед (рис.9).
Объем
этого параллелепипеда равен V
= Sосн..Н
. Но Sосн
= |![]()
![]() |,
а высота Н равна Н =
|,
а высота Н равна Н =
![]() .
Тогда
.
Тогда
V = 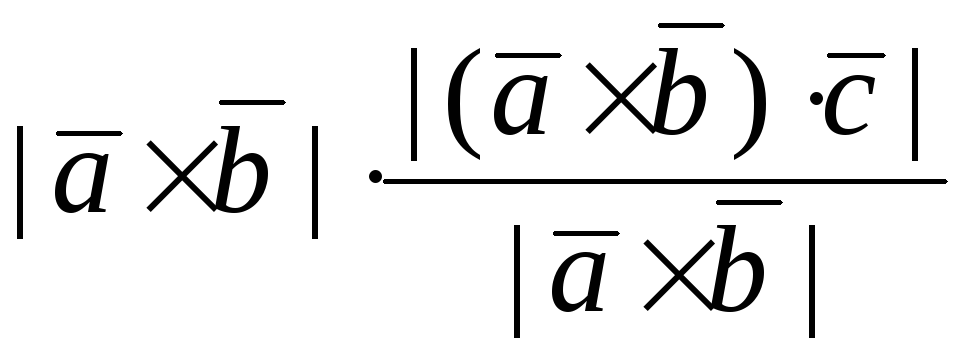 = |(
= |(![]()
![]() ,с)|
= = |
,с)|
= = |![]() .
.![]() .
.![]() |.
|.
Таким образом, если векторыа, b, с некомпланарные, то объем V параллелепипеда, построенного на этих векторах, равен
V= |a .b .c |,
то есть абсолютной величине смешанного произведения этих векторов.
Наряду
со смешанным произведением трех векторов,
можно рассмотреть и произведение вида
![]() (
(![]() с)
– такое произведение называется двойным
векторным произведением.
с)
– такое произведение называется двойным
векторным произведением.
Двойное векторное произведение обладает свойством, которое связывает векторное произведение со скалярным произведением и произведением вектора на число:
![]() (
(![]() с)
= (
с)
= (![]() .
.
![]() )
)![]() – (
– (![]() .
.![]() )
)![]() .
.
