4.2. Прямая на плоскости
Пусть
в ПДСК дана прямая l,
М0 –
некоторая фиксированная точка этой
прямой, а М – текущая точка прямой l.
Обозначим S
произвольный вектор, параллельный этой
прямой (рис.3), а r
=
иr0
= 
–
радиус векторы точек М и М0
в ПДСК. Тогда можно записать
=r
–r0.
Очевидно,
точка М лежит на прямой l
тогда и только тогда, когда вектор
параллелен этой прямой, и, следовательно,
параллелен векторуS.
Значит, должно выполняться условие
=
,
гдеt R
– некоторое число, для каждой точки М
– свое. Следовательно, для точек прямой
l справедливо равенствоr
–r0
=
,
или
r
=r0
+
(1).
Это равенство называется векторным уравнением прямой. Вектор S называется направляющим вектором этой прямой.
Таким образом, всякая прямая может быть однозначно задана точкой (М0) и вектором (параллельным этой прямой).
Мы рассмотрели случай пространственной прямой, но нигде это явно не отражалось. Значит, векторное уравнение (1) определяет как пространственную, так и плоскую прямую.
Рассмотрим ПДСК в R2. Пусть М0(х0, у0), М(х, у), S = (m, n). Из равенства (1) получим (х, у) = (х0, у0) + t(m, n), или
,
(2)
Эти уравнения называются параметрическими уравнениями прямой на плоскости. Если уравнения (2) преобразовать к виду
,
то отсюда следует уравнение
,
(3)
к
оторое
называетсяканоническим
уравнением прямой.
Напомним еще раз, что и в уравнении (3), и в уравнении (2) (х0; у0) – координаты точки, лежащей на прямой, (т; п) – координаты направляющего вектораS этой прямой (вектора, параллельного прямой): Эти уравнения называют также уравнениями прямой, проходящей через заданную точку параллельно заданному вектору.
Если
вектор S
=
,
где М0(х0,
у0)
и М1(х1,
у1)
– точки, лежащие на прямой l,
то S
= (х1
– х0,
у1
– у0),
следовательно, уравнение (3) можно
представить в виде
,
(4)
–
уравнения
прямой, проходящей через
две точки М0(х0
; у0)
и М1(х1;
у1).
Продолжим
преобразование уравнения (3):
п(х – х0) = т( у1 – у0), п(х – х0) – т( у1 – у0) = 0.
Обозначим здесь А = п, В = –т, получим
А(х – х0) + В( у1 – у0) = 0, (5).
ОбозначимN = (А, В). Нетрудно убедиться в том, что векторы N и S ортогональны:
(N,S ) = Ат + Вп = пт + (–т)п = 0.
П
оэтому
уравнение (5) есть уравнение прямой,проходящей через точку
М(х0
; у0)
перпендикулярно вектору
`N = (A
; B). Вектор N,
перпендикулярный заданной прямой,
называется нормальным
вектором этой прямой.
Если в уравнении (5) А и В – произвольные числа, то это уравнение называют уравнением пучка прямых, проходящих через точку М0(х0, у0).
В уравнении (5) раскроем скобки
Ах + Ву +(–Ах0 – Ву0) = 0
и обозначим С = –Ах0 – Ву0. Получим уравнение
Ах + Ву + С = 0, (6)
– общее уравнение прямой. Коэффициенты А и В в общем уравнении определяют координаты нормального вектора этой прямой:N = (A; B) l.
Справедлива теорема:
Теорема 4.1.
Любое уравнение первой степени (линейное) относительно переменных х и у определяет на плоскости прямую линию, и наоборот, любая прямая на плоскости может быть задана линейным уравнением вида
Ах + Ву + С = 0.
Исследуем расположение прямой относительно системы координат по ее общему уравнению Ах + Ву + С = 0.
Е
слиС = 0, А,
В
0, то прямая Ах
+ Ву = 0
проходит через
начало координат
(координаты точки (0, 0) удовлетворяют
этому уравнению, значит, она лежит на
данной прямой).
Если А = 0, а В, С 0, то прямая Ву + С = 0 параллельна оси ОХ (нормальный вектор этой прямой имеет координаты (0,В), т.е. перпендикулярен оси ОХ, поэтому прямая и ось параллельны).
Е
слиВ = 0,
А, С
0, то
прямая Ах
+ С = 0
параллельна оси ОУ (в
этом случае нормальный вектор имеет
координаты (А,
0), т.е. параллелен оси ОХ, и, значит,
перпендикулярен оси ОУ, поэтому и прямая
параллельна оси ОУ)
Если А = 0, С = 0, В 0, то уравнение Ву = 0 определяет ось ОХ (прямая параллельна оси ОХ и проходит через начало координат).
Если В = 0, С = 0, А 0, то уравнение Ах = 0 определяет ось ОУ.
Е
слиВ
0, то Ву
= Ах –
C, или
.
Обозначимk = –
,
а b = – 
,
тогда уравнение (6) примет вид
y = kx + b, (7)
– уравнение с угловым коэффициентом. Коэффициенты k и b имеют простой геометрический смысл:
k = tg, где – угол между прямой и положительным направлением оси ОХ (k называют угловым коэффициентом прямой),
b – ордината точки пересечения прямой с осью ОУ (величина отрезка, отсекаемого прямой на этой оси). Если k = 0, то прямая параллельна оси ОХ; если b = 0, то прямая проходит через начало координат.
Если С 0, то Ах + Ву = –С, откуда
,
или 
.
О
бозначим
здесьа
= – 
,
b = – 
,
получим
,
(8)
уравнение прямой в отрезках на осях.
Уравнение получило такое название, исходя из геометрического смысла чисел а и b:
а – величина отрезка, отсекаемого прямой на оси ОХ,
b – величина отрезка, отсекаемого прямой на оси ОУ.
Таким образом, прямая (8) проходит через точки (0 ; b) и (а ; 0).
Из всего вышесказанного можно сделать следующий вывод:
чтобы найти уравнение прямой, достаточно знать:
либо две точки этой прямой (уравнение(4))
либо точку и вектор – параллельный этой прямой (направляющий, уравнения (1), (2) (3)) или перпендикулярный этой прямой (нормальный, уравнение (5) или (6)).
И
сследовать
взаимное расположение
прямых на плоскости
можно с помощью соответствующих им
векторов и точек, принадлежащих этим
прямым. Если N1,
S1
– нормальный и
направляющий векторы прямой l1
соответственно, а N2,
S2
– нормальный и
направляющий векторы прямой l2,
то
l1|| l2 N1 ||N2, илиS1||S2, или N1S2 (рис. а);
l
б)
1l2 N1 N2,илиS1S2,илиN1||S2(рис.б);
l1 = l2 l1|| l2 и существует точка М:
М
l1 ,
Мl2;
угол между прямыми можно найти как угол между соответствующими им векторами:
(либо как смежный к этим углам),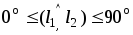 
(рис.в);координаты точки М пересечения двух прямых есть решение системы уравнений этих прямых.
Расстояние
d от
точки М(х0;
у0)
до прямой
Ах + Ву
+ С = 0
находят по формуле
Действительно,
пусть М1(х1,
у1)
произвольная точка этой прямой, а N
=(А, В)
– ее нормальный вектор. Тогда расстояние
d =
=
.
Поскольку
=
(х0
–х1,
у0
– у1),
то
d
=
=
= 
Т.к.
точка М1
l, то Ах1
+Ву1+
С = 0, откуда –Ах1
–Ву1=
С . Тогда получаем d
=
.
Замечание: Если М0(0,0), то d = |С|, т.е. коэффициент С в общем уравнении прямой характеризует отклонение прямой от начала координат.