Единственным эффективным нетепловым механизмом испарения светом металлических островков может быть только фотоатомная эмиссия, квантовый выход которой порядка 10−6. Так как при фотоатомной эмиссии и нагреве подложки кинетика уменьшения островков одинаковая (в обоих случаях атомы испаряются в вакуум с поверхности островка), то обнаруженное различие действия света разного спектрального состава на пленку можно связать только с различием этого действия на островки разной формы.

При резонансе частоты излучения с частотой плазменных колебаний островка действующее на его поверхности поле усиливается, что усиливает и эффективность фотоатомной эмиссии. Частоты плазменных мод зависят от формы островка, причем у сильно вытянутых и сплющенных островков есть мода, значительно смещенная в красную сторону от соответствующей частоты шарообразного островка.

Обнаруженную селективность действия длинноволнового излучения можно связать с сильно деформированными островками. Резонансное воздействие на них вызывает заметное изменение формы у сильно деформированных островков благодаря наибольшему усилению светового поля на заостренностях формы, где ускоренная фотоатомная эмиссия вызывает сглаживание и уменьшение деформации. В результате этого уменьшается дисперсия распределения островков по форме, что и обнаруживается в эксперименте как заметное изменение величины mv2 при малых изменениях объема основной массы островков. Широкополосное оптическое излучение, действующее на островки различной формы одинаковым образом, селектирующими свойствами не обладает и действует примерно так же, как и нагрев подложки.

5.5.2.Измерение релаксационных параметров индивидуальных резонансов в неоднородных системах

Линейная спектроскопия широко используется для определения характеристик металлических наночастиц. Громадный объем информации о структуре и динамике свободных, взвешенных и осажденных на поверхность наночастиц был получен путем исследования их спектров экстинкции. В то же время линейная спектроскопия не может быть использована для однозначного определения такого важного параметра, как время дефазировки плазмонного резонанса. Дело в том, что неоднородное уширение вносит неконтролируемый вклад в спектральную ширину резонанса. Таким образом, по ширине спектров поглощения можно определить лишь нижнюю границу времени жизни плазмона, которая при значительном неоднородном уширении, характерном для большинства методов приготовления металлических наночастиц, оказывается, по сути, бесполезной. Несколько лет назад появились работы, в которых для однозначного определения времени жизни плазмона предлагалось использовать автокорреляционную методику, основанную на генерации второй и третьей гармоник падающего на кластеры излучения. При этом считалось, что подобные измерения, выполненные с интерференционной точностью при использовании фемтосекундных лазерных импульсов, дают воз-

294 А.М. Бонч-Бруевич, Т.А. Вартанян, С.Г. Пржибельский

можность непосредственно измерить время жизни плазмона по увеличению ширины автокорреляционной функции второй гармоники, полученной от кластеров, по сравнению с длительностью импульса, определенной из подобного же эксперимента с нелинейным кристаллом, отклик которого можно считать мгновенным [35, 36]. Однако непосредственный расчет автокорреляционной функции излучения второй гармоники [37] показал, что неоднородное уширение существенно сказывается и на этом методе измерения времени жизни плазмона. Более того, между линейными спектрами поглощения и автокорреляционными функциями второй и третьей гармоник при произвольном неоднородном распределении резонансных частот имеется интегральное соотношение, в принципе позволяющее рассчитать одну характеристику через другую [38].

Влияние неоднородного уширения на достоверность результатов измерения времени дефазировки поверхностного плазмона по автокорреляционной методике

Линейная спектроскопия состоит в измерении спектра экстинкции, который в случае малых металлических частиц определяется поглощением в них падающего излучения. Моделируя резонансные оптические свойства плазмона с помощью классического гармонического осциллятора, имеющего собственную частоту и постоянную затухания , запишем уравнение движения коллективной координаты x в виде

где ! – частота падающего излучения, а f˜(t) пропорциональна его амплитуде. Безразмерная постоянная, связывающая f˜(t) и амплитуду поля, обычно записывается в виде e=m, где e – заряд, а m – масса электрона. Коллективные колебания, описываемые уравнением (5.2), можно представить себе как смещение центра масс всех электронов относительно однородного положительно заряженного фона, представляющего собой покоящиеся атомные остатки металлической частицы. Установившееся решение уравнения (5.2) при f˜(t) = const, имеет вид x = x0 exp(−i!t), где амплитуда колебаний x0 представляется в виде

Когда частота падающего излучения ! приближается к собственной частоте локализованного плазмона , а именно, если выполнено неравенство

наблюдается хорошо известный резонанс в сечении поглощения, если, конечно, ширина резонанса много меньше резонансной частоты, то есть

В окрестности резонанса, когда выполнены оба неравенства (5.4) и (5.5), выражение (5.3) можно упростить

Выражение (5.6) можно вывести непосредственно из упрощенного варианта уравнения движения, справедливого в окрестности резонанса:

где f (t) = i f˜(t)=2 . Для справедливости (5.7) необходимо не только, чтобы выполнялись неравенства (5.4) и (5.5), но и чтобы f (t) изменялась не слишком быстро. Более точно, для лазерного импульса с длительностью должно выполняться следующее неравенство:

! 1 ;

означающее, что импульс должен состоять из достаточно большого числа оптических периодов.

Решение (5.6), полученное для случая, когда f (t) постоянно, остается справедливым и при изменяющемся f (t), если только изменение происходит достаточно медленно. В этом случае можно говорить о мгновенном следовании амплитуды колебаний за амплитудой действующего поля. Отклонение от мгновенного следования, которое становится заметным при более быстром изменении амплитуды действующего поля, можно оценить величиной относительной ошибки, составляющей

Таким образом, существует широкий интервал длительностей импульсов

(2 )−1 ≤ −1 ;

в котором уравнение (5.7) справедливо, но для описания поведения системы при резонансном возбуждении нельзя ограничиться установившимся решением (5.6).

Идея автокорреляционных измерений времени дефазировки плазмонных колебаний в металлических наночастицах [35, 36] основана на оценке (5.8). Если считать, что время дефазировки составляет примерно 10 фс, то при использовании лазерных импульсов с длительностью около 50 фс, настроенных в резонанс с плазмоном, можно ожидать относительного отклонения от мгновенного следования, составляющего до 20%, то есть легко измеримую величину. Анализ автокорреляционной методики, проведенный в [37], основан на решении уравнения (5.7), дополненного нелинейным членом ax2,

296 А.М. Бонч-Бруевич, Т.А. Вартанян, С.Г. Пржибельский

который описывает слабый ангармонизм коллективных колебаний. Предполагается, что постоянная a достаточно мала, чтобы нелинейный член, описывающий генерацию второй гармоники, можно было учесть по теории возмущений следующим образом. Сперва решается уравнение (5.7) без возмущающего члена, и его решение подставляется в ax2. Затем это же уравнение решается вновь с вычисленным уже ангармоническим членом в качестве вынуждающей силы. Поскольку фундаментальная частота падающего поля и его вторая гармоника не могут одновременно быть в резонансе с плазмонным колебанием, представляют интерес два случая, когда к собственной частоте плазмонных колебаний близка либо частота падающего поля, либо частота второй гармоники. Для нерезонансной частоты отклик системы можно считать мгновенным, в то время как при резонансном возбуждении необходимо пользоваться переходным решением уравнения (5.7).

При автокорреляционных измерениях на систему последовательно действуют два одинаковых лазерных импульса, один из которых задержан относительно другого на время T , которое можно изменять. Если через g(t) обозначить зависящую от времени амплитуду первого импульса, то амплитуду суперпозиции двух наложенных импульсов можно представить в виде

f (t) = g(t) + exp(i!T )g(t − T ) :

Если нелинейная среда, используемая для генерации второй гармоники, не имеет резонансов ни на частоте падающего поля, ни на частоте второй гармоники, то ее нелинейный отклик можно считать мгновенным. В этом случае амплитуда второй гармоники E(t) пропорциональна квадрату амплитуды падающей волны [ f (t)]2. Измеряемой в эксперименте величиной является автокорреляционная функция S (T ), описывающая зависимость интегральной интенсивности второй гармоники от времени задержки между импульсами

T ,

Z∞

S (t) = |E(t)|2dt :

−∞

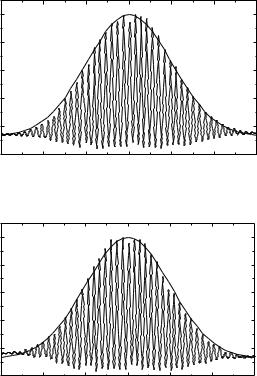
Если задержка T превышает длительность импульса , то S (T ) сводится к сумме двух равных вкладов от каждого из импульсов. С другой стороны, при нулевой задержке амплитуда действующего поля увеличивается вдвое, а интенсивность второй гармоники увеличивается при этом в 16 раз по сравнению с интенсивностью, получаемой от одиночного импульса. Очевидно, что ширина автокорреляционной функции S (T ) служит хорошей мерой длительности импульса. На рис. 5.9 приведена нормированная теоретическая автокорреляционная функция и ее верхняя и нижняя огибающие. Расчет выполнен для гауссовых импульсов с временной зависимостью exp(−t2=2) при= 26 фс. Оптическая частота соответствует длине волны = 820 нм. Горизонтальная линия, проведенная на уровне 0.125, является асимптотой для всех трех кривых. Быстрые осцилляции S (T ) обусловлены интерференцией между двумя импульсами.

298 А.М. Бонч-Бруевич, Т.А. Вартанян, С.Г. Пржибельский

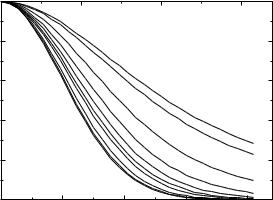
Влияние скорости дефазировки на автокорреляционную функцию можно увидеть следующим образом. Если скорость дефазировки велика по сравнению с обратной длительностью импульса, то внешнее интегрирование эффективно ограничено очень малыми значениями s, что в свою очередь сводит внутренний интеграл к величине, очень близкой к [ f (t)]2, характерной для нерезонансного случая. Если же скорость дефазировки сравнима или меньше обратной длительности импульса, внешнее интегрирование в (5.10) захватывает достаточно большие значения s, так что подынтегральная функция во внутреннем интеграле равна произведению амплитуд в два различных момента времени, а не квадрату амплитуды [ f (t)]2. Это приводит к лучшему перекрыванию, а следовательно, и к большим значениям автокорреляционной функции при временах задержки, превосходящих длительность лазерного импульса. Таким образом, автокорреляционная функция второй гармоники, полученной в резонансной среде, оказывается уширенной по сравнению с автокорреляционной функцией второй гармоники, генерированной в нерезонансной среде. На рис. 5.10 показана верхняя огибающая автокорреляционных функций при различных скоростях дефазировки, рассчитанных для случая, когда частота падающего излучения совпадает с частотой плазмонного резонанса в металлических наночастицах ! = .

Рис. 5.10. Верхняя огибающая автокорреляционных функций, рассчитанных для случая, когда частота падающего излучения совпадает с частотой плазмонных резонансов в металлических наночастицах ! = . Неоднородное уширение отсутствует, = 0. Кривые соответствуют следующим значениям безразмерного параметра : 0.6, 0.72, 1.2, 1.8, 2.4, 3.0, 3.6, 4.8, 6.0, 12.0. Нижняя кривая совпадает с автокорреляционной функцией лазерного импульса, которая может быть получена в нерезонансной нелинейной среде.

300 А.М. Бонч-Бруевич, Т.А. Вартанян, С.Г. Пржибельский

Внимательное рассмотрение выражений (5.13) и (5.14) показывает, что дисперсия неоднородного распределения собственных частот играет теперь ту же роль, что и скорость дефазировки . Даже в том случае, если время жизни плазмона неограниченно велико ( =0), изменение s в (5.13) или t′ в (5.14) ограничено величиной 2 −1, то есть обратной шириной неоднородного распределения собственных частот. Следовательно, если амплитуда лазерного импульса не изменяется заметно за время 2 −1, автокорреляционная функция будет примерно такой же, как и в нерезонансном случае, независимо от скорости дефазировки.

Рис. 5.11. Верхние огибающие автокорреляционных функций, рассчитанных для случая, когда частота падающего излучения совпадает с частотой плазмонных резонансов в металлических наночастицах ! = 0. Время жизни плазмонного возбуждения считается бесконечно большим = 0. Кривые соответствуют следующим значениям безразмерного параметра : 0.6, 0.9, 1.2, 1.5, 1.8, 2.4, 3.0, 3.6, 4.2, 4.8. Нижняя кривая совпадает с автокорреляционной функцией лазерного импульса, которая может быть получена в нерезонансной нелинейной среде.

1

На рис. 5.11 приведены верхние огибающие автокорреляционных функций, рассчитанных для случая, когда частота падающего излучения близка к собственным частотам плазмонных резонансов в металлических наночастицах = 0. Время жизни плазмонного возбуждения считается бесконечно большим = 0. Кривые соответствуют различным ширинам неоднородного распределения собственных частот. Сравнивая рис. 5.10 и 5.11, видим, что одинаковые ширины и очень близкие формы автокорреляционных функций получаются для совершенно различных комбинаций однородных и неоднородных ширин. В общем случае, когда отличны от нуля и , и , ширину

верхней огибающей автокорреляционной функции t можно качественно оценить, приравняв показатель экспоненты в подынтегральном выражении (5.13) к константе, близкой к единице,

Количественные результаты были получены непосредственным численным определением ширины автокорреляционной функции, рассчитанной по формуле (5.13), как функции двух переменных – однородной ширины плазмонного резонанса и дисперсии неоднородного распределения собственных частот. Результаты расчета представлены на рис. 5.12. Кривые на рисунке близки к параболам (5.15). Из полученных результатов следует, что неод-

Рис. 5.12. Зависимости уширения верхней огибающей автокорреляционной функции от времени дефазировки плазмона −1 и ширины неоднородного распределения собственных частот в случае резонансного возбуждения ! = 0. Цифры около кривых

– величины уширения в процентах. В скобках приведены абсолютные уширения t. По оси абсцисс отложено произведение неоднородной ширины на длительность импульса .

нородное уширение уменьшает ширину автокорреляционной функции таким образом, что однозначное определение времени дефазировки плазмонного резонанса становится невозможным. При большой ширине неоднородного распределения собственных частот уширение автокорреляционной функции становится настолько малым, что не может быть определено экспериментально. В верхней части рис. 5.13 [37] показаны автокорреляционные функции, полученные от наночастиц калия с большой дисперсией собственных частот, а в нижней, для сравнения – нерезонансный сигнал второй гармоники, полу-

302 А.М. Бонч-Бруевич, Т.А. Вартанян, С.Г. Пржибельский

ченный от нелинейного кристалла. Верхняя огибающая построена для тех же параметров, что и на рис. 5.9. Видно, что, несмотря на резонансный характер взаимодействия падающего излучения с наночастицами, уширение автокорреляционной функции в пределах экспериментальной точности не наблюдается.

T, ôñ

Рис. 5.13. Автокорреляционные функции, полученные от наночастиц калия (вверху) и нерезонансный сигнал второй гармоники, полученный от нелинейного кристалла (внизу). Верхняя огибающая построена для тех же параметров, что и на рис. 5.9.

Универсальная связь между линейными спектрами поглощения и результатами автокорреляционных измерений

Расчет автокорреляционной функции, выполненный в предыдущем подразделе, был основан на конкретном виде неоднородного распределения собственных частот плазмонных резонансов в металлических наночастицах. Здесь бу-

дет выведено общее соотношение, связывающее автокорреляционную функцию с линейным спектром поглощения для произвольного распределения собственных частот [38].

Уравнению движения коллективной координаты (5.7) отвечает лоренцев контур линейного поглощения

полуширина которого на половине высоты равна . Таким образом, в отсутствие или при малом неоднородном уширении по сравнению с затухание можно получить непосредственно из линейного спектра экстинкции. В то же время при большом неоднородном уширении его учет становится необходимым. Пусть G( ) будет нормированной функцией распределения резонансных частот:

Z

G( )d = 1 :

В предыдущем подразделе была использована гауссова функция распределения с центральной частотой 0 и дисперсией , для которой G( ) имеет вид

Спектр поглощения неоднородного ансамбля можно получить, проинтегрировав спектр поглощения отдельного осциллятора (5.16) по распределению частот G( )

В этом случае спектральная ширина линии поглощения определяется не только затуханием отдельного осциллятора, но и дисперсией неоднородного распределения частот. В предельном случае очень широкого неоднородного распределения уравнение (5.17) приводит к S (!) G(!) и спектр поглощения не содержит информации о затухании отдельного осциллятора.

Для учета неоднородного уширения формулу (5.10) необходимо усреднить по распределению частот G( ). В результате правая часть (5.10) принимает вид

где

Z∞

A(s) = exp[−( − i )s]d :

−∞

304 А.М. Бонч-Бруевич, Т.А. Вартанян, С.Г. Пржибельский

Непосредственным вычислением можно показать, что при значениях s > 0, которые только и входят в (5.18), A(s) пропорционально фурье-образу спектра S (!), полученного в (5.17),

−∞

Таким образом, если известен спектр линейного поглощения, то с помощью выведенных выше уравнений можно рассчитать автокорреляционную функцию второй гармоники. Строго говоря, это означает, что в автокорреляционной функции второй гармоники не содержится никакой дополнительной информации о системе по сравнению со спектром линейного поглощения. Этот вывод получен здесь без каких-либо предположений о конкретной форме неоднородного уширения и не зависит от нее.

Несмотря на все сказанное выше, с точки зрения эксперимента, автокорреляционные измерения могут быть в некоторых случаях полезны. Дело в том, что как спектр поглощения, так и автокорреляционная функция могут быть надежно измерены лишь в своих центральных частях вблизи соответствующих максимумов. Крылья из-за меньшего отношения сигнала к шуму измеряются с большей погрешностью. С этой точки зрения автокорреляционные измерения могут дать дополнительную информацию о системе по сравнению с линейной абсорбционной спектроскопией, поскольку надежно измеряемая центральная часть автокорреляционной функции определяется крыльями линейного спектра поглощения. Действительно, согласно равенству (5.18) центральная часть автокорреляционной функции определяется значениями A(s) при s, меньших длительности импульса. В то же время, согласно (5.19) эти значения A(s) существенным образом определяются всем спектром S (!), включая далекие крылья, где данные линейной спектроскопии наименее надежны. Подобным же образом центральная часть спектра поглощения определяет значения A(s) при s, больших −1, которые в свою очередь определяют трудно измеряемые крылья автокорреляционной функции. Эти соображения оправдывают попытки комбинации результатов линейной абсорбционной спектроскопии и автокорреляционных измерений для определения времени затухания плазмонного резонанса. Проведенный выше анализ показывает, однако, что однозначное определение времени затухания из таких измерений возможно только при том условии, что характер неоднородного распределения собственных частот известен из независимых измерений.

Выжигание постоянных провалов в спектрах поглощения ансамблей металлических наночастиц

В предыдущем разделе было показано, что автокорреляционная методика не позволяет измерять время дефазировки в условиях сильного неоднородного уширения. В нелинейной оптике известно несколько стандартных методов

исключения неоднородного уширения. К ним относятся резонансная флуоресценция, фотонное эхо, выжигание спектральных провалов [39]. До самого последнего времени ни одна из указанных нелинейно-оптических методик не применялась для исследования дефазировки поверхностных плазмонов, локализованных в нанометровых металлических частицах. Первым был реализован метод измерения скорости дефазировки поверхностных плазмонов, основанный на выжигании постоянных спектральных провалов. Хотя возможность селективной фотомодификации металлических наночастиц была известна из экспериментов на коллоидных системах [40–42], развитие метода потребовало создания соответствующего теоретического аппарата, так как выжигание постоянных спектральных провалов в ансамблях металлических наночастиц, сформированных на диэлектрических подложках, имеет ряд особенностей, которые не встречаются при применении этого метода к другим системам.

Прежде чем излагать идею метода, необходимо более подробно описать систему, для исследования которой он предназначен. Металлические наночастицы выращиваются на прозрачной диэлектрической подложке путем осаждения на ее поверхность атомов металла. Атомы, адсорбированные на поверхности, диффундируют по ней и образуют зародыши металлической фазы, которые затем вырастают в наночастицы. Хотя средним размером частиц металла можно управлять с помощью времени осаждения, образующиеся частицы имеют различные размеры и формы. Между размером и формой частиц, выросших в таких условиях, существует определенная корреляция, которая была установлена с помощью атомно-силовой микроскопии и линейной спектроскопии [43]. Маленькие частицы имеют почти шаровую форму, в то время как более крупные частицы сплюснуты в перпендикулярном к поверхности направлении. Наибольший интерес представляют металлические наночастицы с размерами, много меньшими длины волны излучения, соответствующего собственной частоте коллективных возбуждений. Причина этого состоит в том, что потери на излучение растут вместе с объемом частицы, так что время жизни поверхностных плазмонов, локализованных в крупных частицах, мало, а следовательно, и добротность резонансов в таких частицах мала. Собственные частоты поверхностных плазмонов, локализованных в частицах, размеры которых много меньше длины волны, не зависят от их размера, а определяются только их формой. В довольно грубом, но достаточном для наших целей приближении форму частицы можно охарактеризовать отношением полуосей наиболее близкого к ней по форме сплюснутого эллипсоида. В отличие от сферы, имеющей одну собственную частоту плазмонных колебаний, эллипсоид вращения имеет две собственные частоты коллективных возбуждений, одна из которых выше, а другая ниже собственной частоты плазмонных колебаний сферы. При нормальном падении излучения, а также при наклонном падении s-поляризованного излучения электрический вектор параллелен поверхности, так что возбуждается только низкочастотная мода, соответствующая коллективным колебаниям электронов вдоль длинной оси эллипсоида.

306 А.М. Бонч-Бруевич, Т.А. Вартанян, С.Г. Пржибельский

Таким образом, весь ансамбль частиц, сформированных на подложке, можно охарактеризовать функцией распределения по собственным частотам коллективных возбуждений. Как правило, это распределение оказывается намного шире, чем однородная ширина резонансов, так что ширина спектра экстинкции всего ансамбля частиц определяется именно неоднородным распределением резонансных частот, а не временем дефазировки локализованных плазмонов. Для теоретического описания метода измерения времени дефазировки локализованных плазмонов необходимо прежде всего параметризовать спектр экстинкции неоднородно уширенного ансамбля возможно более общим образом.

Обозначим сечение поглощения металлической наночастицы с собственной частотой и объемом V на частоте ! через (!; ). Если принять, что оптические свойства металла описываются зависящей от частоты комплексной диэлектрической постоянной " = "1 +i"2 , то квазистатическое выражение

где c – скорость света. В том случае, если металл хорошо описывается моделью Друде с плазменной частотой !p и затуханием , диэлектрическая постоянная имеет простой аналитический вид

если только и |!− | . В этом случае сечение поглощения имеет лоренцев спектральный контур, ширина которого не зависит от собственной частоты металлической наночастицы. Такая форма спектральной зависимости сечения поглощения полностью соответствует представлению о локализованном плазмоне как о гармоническом осцилляторе с затуханием. Это представление можно обобщить на реальные металлы, диэлектрическая постоянная которых может сильно отличаться от (5.21), если определить зависящую от частоты ширину плазмонного резонанса согласно [1] как

Тогда для частот !, близких к собственной частоте плазмона , уравнение (5.20) можно записать как

Это выражение подобно (5.22), за исключением того, что теперь спектральная ширина резонанса и максимальное значение сечения поглощения зависят от собственной частоты плазмона, которая в свою очередь определяется формой металлической наночастицы. Использование выражения (5.25) оправдано до тех пор, пока изменяется незначительно при изменении на ± , то есть, если | ± − | . Это условие нарушается во всяком случае при тех частотах, при которых "1( ) достигает экстремума и ширина , определенная в (5.23), стремится к бесконечности.

Уравнение (5.25) можно обобщить еще больше, заменив ширину на феноменологический параметр hom( ). Эта ширина всегда больше, чем и включает в себя, помимо учтенных в (5.23), все остальные механизмы уширения, такие как рассеяние электронов при столкновениях с поверхностью наночастицы, уширение, связанное с химическим окружением, и радиационные потери.

Спектр поглощения всего ансамбля частиц дается выражением

где f ( ) – функция распределения собственных частот плазмонных резонансов, обусловленная различием форм частиц. Подставляя в (5.26) (!; ) из (5.25), получим спектр поглощения до лазерного воздействия в виде

Следующий шаг состоит в расчете температуры, которой достигают металлические наночастицы при лазерном воздействии. Будем считать, что вся поглощенная наночастицей световая энергия превращается в тепло. Так как подложка прозрачна для действующего излучения, она нагревается только за счет тепла, идущего от металлических наночастиц. Если иметь в виду использование наносекундных лазерных импульсов, то расчет температурных полей можно проводить, считая частицу точечным источником на поверхности полубесконечной среды, причем интерес представляет только установившийся температурный режим. Если плотность энергии в лазерном импульсе обозначить через F, а длительность импульса через , то подъем температуры частицы, имеющей собственную частоту , под действием лазерного излучения с частотой L можно записать как C F ( L; ) , где

308 А.М. Бонч-Бруевич, Т.А. Вартанян, С.Г. Пржибельский

– константа, определяемая теплопроводностью подложки и радиусом контактной площадки между частицей и подложкой R [44]. Если начальную температуру обозначить T0 , то температура во время облучения

Если подъем температуры достаточно велик, то различные термически активированные процессы могут приводить к изменению объема и формы наиболее нагретых частиц. Рассмотрим, прежде всего, испарение атомов. Скорость испарения атомов и получающееся в результате испарения изменение объема частиц пропорциональны экспоненциальному фактору exp[−Ea=kBT ( )] , где Ea – энергия активации испарения, а kB – постоянная Больцмана. Предполагая, что процесс испарения описывается кинетикой первого порядка с предэкспоненциальным фактором , который имеет порядок характерной частоты колебаний 1012 с−1, для пропорционального объему максимального сечения поглощения получим уравнение

Если времена освещения малы, так что и изменения объема малы, то изменение максимального сечения поглощения

где a( ) = 0( ) меняется при изменении гораздо медленнее, чем экспоненциальный активационный фактор. Вообще говоря, испарение может приводить и к изменению формы частиц, а следовательно, и к сдвигу собственной частоты коллективных колебаний электронов на некоторую величину . Для естественно использовать выражение, аналогичное (5.31). Если изменение формы в большей мере обусловлено поверхностной диффузией атомов, а не их испарением, то энергия активации, входящая в выражение для, может отличаться от энергии активации испарения. Обозначим энергию активации, соответствующую изменению формы частиц, через Eb. Тогда

где b( ) – функция , медленно меняющаяся по сравнению с экспоненциальным фактором. Подставляя новые значения максимального сечения поглощения и собственной частоты в уравнение (5.27), получим спектр поглощения ансамбля частиц после лазерного воздействия

Z

S 2(!) = f ( )[ 0( ) + 0( )] (! − − )2 + ( hom( )=2)2 d : (5.33)

Форма спектрального провала определяется разностью спектров поглощения после и до лазерного воздействия

Из проведенного расчета очевидно, что наибольшие изменения объема и формы претерпевают те частицы, собственные частоты которых близки к частоте лазерного излучения. Вследствие этого можно ожидать, что ширина разностного спектра окажется близкой к однородной ширине резонанса в тех частицах, собственная частота которых совпадает с частотой лазерного излучения.

Ограничиваясь случаем малых изменений 0( ) и , получим

Для того чтобы сделать следующий шаг, необходимо более подробно рассмотреть экспоненциальные функции в выражениях (5.31) и (5.32). Начнем с

которые соответствуют начальной температуре и максимальному увеличению температуры в ходе облучения. С помощью этих величин экспоненциальная функция запишется следующим образом:

при = L . Поскольку 0a считается много меньшей единицы, а Ia того же порядка, что и 0a или больше, то экспоненциальная функция (5.39) при, L убывает очень быстро. Эффективная ширина области, в которой она принимает значения, сравнимые с максимальным (5.40), описывается неравенством

вкладов различной четности. Первый, четный, вклад описывает уменьшение объема резонансных частиц за счет испарения. Второй, нечетный, вклад вызван изменением формы резонансных частиц, которое в основном сводится к тому, что частица становится менее сплюснутой. Собственная частота при

этом возрастает. Постоянные ˜ и ˜ определяют вклады четного и нечетно-

A B

го контуров в общую форму разностного спектра, который мы по-прежнему будем называть провалом, хотя он может иметь и более сложную, знакопеременную, структуру. В использованном здесь приближении ширина провала равна однородной ширине резонанса, в то время как в большинстве обычных применений техники выжигания провалов ширина провала вдвое больше однородной ширины. Такое различие возникает из-за особой селективности термически активированных процессов фотомодификации. Этот вывод справедлив только при очень низких интенсивностях лазерного воздействия.

При увеличении интенсивности лазерного воздействия ширина провалов увеличивается, так как за счет нерезонансного поглощения в крыльях в процессы фотомодификации вовлекаются частицы, собственные частоты которых лежат все дальше от частоты лазерного излучения. Формально уравнение (5.51) справедливо в пределе, когда полевые ширины Ia и Ib много меньше однородной ширины hom( L). В действительности полевые ширины не могут быть сделаны как угодно малыми ни при каких интенсивностях лазерного воздействия. Согласно (5.42), отношение Ia=hom( L) достигает минимального значения √ 0a, когда Ia = 0a. Более того, с точки зрения эксперимента повышение интенсивности воздействия может оказаться желательным для увеличения отношения сигнала к шуму. Для того чтобы результаты измерений при значительных полевых уширениях можно было использовать для определения однородной ширины резонансов, полученные из эксперимента ширины провалов необходимо экстраполировать к нулевым интенсивностям лазерного воздействия. С этой целью интегралы (5.44) и (5.46) были рассчитаны более точно с учетом конечной ширины экспоненциальных функций. При этом оказалось возможным учесть также и медленную зависимость от

частоты других членов, входящих в (5.44) и (5.46), а именно, ¯ и ¯ .

A( ) A( )

Если эту зависимость моделировать гауссовыим функциями с центральными

Удобство такого выбора заключается в возможности представить произведение двух гауссовых функций как одну гауссову функцию с центральной частотой и дисперсией, определенными формулами

312 А.М. Бонч-Бруевич, Т.А. Вартанян, С.Г. Пржибельский

[ ]

Величины A* и B* не зависят от !. Интеграл (5.56), известный в атомной спектроскопии как фойгтовский контур, может быть выражен через интеграл вероятностей от комплексного аргумента [45]. Интеграл (5.57), также может быть выражен через интеграл вероятностей от комплексного аргумента. При небольших величинах A=hom и B=hom спектральные профили S a и S b близки к (5.49) и (5.50) соответственно, так что их можно представить в виде, подобном (5.51):

где A и B можно выразить через A* и B* соответственно. Эффективные ширины a и b четного и нечетного контуров, входящих в (5.58), отличаются от однородной ширины плазмонного резонанса hom( L) на малые величины, пропорциональные A и B :

Полученные выражения представляют теоретическую основу [46, 47] применения техники выжигания спектральных провалов для определения однородной ширины плазмонных резонансов в металлических наночастицах. Вариацией параметров функция (5.58) подгоняется к разностным спектрам, измеренным при различных интенсивностях лазерного воздействия, а определенные таким образом эффективные ширины используются для определенияhom( L) путем экстраполяции к нулевой интенсивности лазерного воздействия. Если индуцированное освещением увеличение температуры частиц заметно превышает начальную температуру, а полевая ширина остается меньше однородной, то в соответствии с (5.59) экстраполяция будет линейной.

Первое применение техники выжигания постоянных спектральных провалов для определения времен дефазировки поверхностных плазмонов, локализованных в металлических наночастицах, было описано в [46]. Дальнейшие применения опубликованы в [47–52].

На рис. 5.14 приведены спектры экстинкции наночастиц серебра на сапфировой подложке до и после облучения. Средний радиус частиц составлял около 10 нм. Для частиц такого размера вклад рассеяния в ослабление проходящего излучения мал, так что спектр экстинкции практически полностью обусловлен поглощением. Длительность импульсов излучения, полученного от оптического параметрического генератора, составляла 2–4 нс, а энергия фотонов 2.93 эВ была близка к максимуму поглощения неоднородно уширенной полосы при 2.91 эВ. Изменения в спектре экстинкции надежно регистрировались уже при плотности энергии в импульсе 26 мДж/см2. Эксперимент подтверждает теоретический вывод о возможности селективной фотомодификации металлических наночастиц. Изменения поглощения наблюдаются только для тех частиц, собственные частоты которых близки к частоте лазера. При увеличении плотности энергии в импульсе спектральная область, в которой изменяется поглощение, расширяется.

На рис. 5.15 показан разностный спектр, полученный при плотности энергии в импульсе 30 мДж/см2. Асимметричный контур имеет минимум -1.3 % при 2.85 эВ. Затем следует область увеличения поглощения с максимумом 0.75% при 3.05 эВ. Аналогичные кривые получаются при других плотностях энергии в импульсе. Теоретическая модель (5.58) хорошо воспроизводит форму разностного спектра. Для сокращения числа подгоночных параметров можно было положить a = b = и a = b без заметного ухудшения качества подгонки.

Полученные в результате подгонки значения приведены на рис. 5.16 в зависимости от плотности энергии в импульсе. Эксперимент подтверждает

Рис. 5.15. Разностный спектр экстинкции до и после облучения лазерными импульсами с плотностью энергии 30 мДж/см2 (кружки). Сплошной линией показана теоретическая кривая (5.58), наилучшим образом подходящая к экспериментальным данным. Пунктирная и штриховая линии дают вклады четного и нечетного контуров по отдельности.

Рис. 5.16. Зависимость эффективной ширины разностного спектра (в мэВ) от плотности энергии в импульсе лазерного излучения. Однородная ширина определяется путем линейной экстраполяции результатов измерений По оси абсцисс отложена плотность энергии в импульсе в мДж/см2.