
- •1. Фотонные кристаллы
- •1.1. Концепция
- •1.1.1. Электроны в кристаллических структурах
- •1.1.2. Электромагнитные волны в кристаллических структурах
- •1.1.3. Фотонное твердое тело: распространение и локализация электромагнитных волн в условиях сильного многократного рассеяния
- •1.2. Синтез и свойства фотонных кристаллов
- •1.2.1. Фотонные кристаллы в природе
- •1.2.2. Одномерные периодические структуры
- •1.2.3. Двумерные периодические структуры
- •1.2.4. Трехмерные периодические структуры
- •1.3. Испускание и рассеяние излучения в фотонных кристаллах: роль плотности фотонных состояний
- •1.3.1. Интегральная и локальная плотности состояний
- •1.3.2. Спонтанное испускание фотонов
- •1.3.3. Тепловое излучение
- •1.3.4. Комбинационное рассеяние
- •1.3.5. Резонансное (релеевское) рассеяние
- •1.4. Заключение
- •Список литературы
- •2. Оптическое излучение в линейных и нелинейных периодических структурах
- •2.1. Введение
- •2.2.1. Квазиоптическое приближение
- •2.2.2. Линзовые волноводы и лазерные резонаторы
- •2.2.4. Мелкомасштабная самофокусировка в периодических системах
- •2.2.5. Квазисинхронное параметрическое взаимодействие
- •2.3. Одномодовый световод с брэгговской решеткой
- •2.3.1. Двунаправленное распространение излучения
- •2.3.2. Брэгговские солитоны
- •2.3.3. Оптическая бистабильность и переключение
- •2.3.4. Полупроводниковые микрорезонаторы
- •2.4. Связанные световоды
- •2.5. Двумерные фотонные кристаллы
- •2.5.1. Неидеальные фотонные кристаллы
- •2.5.2. Нелинейные двумерные фотонные кристаллы
- •2.6. Заключение
- •Список литературы
- •3. Оптика квантовых ям и сверхрешеток
- •3.1. Классификация гетероструктур
- •3.2. Размерное квантование электронных состояний
- •3.3. Правила отбора при оптических переходах
- •3.3.1. Междузонные и внутризонные оптические переходы между подзонами размерного квантования
- •3.3.2. Поляризационные свойства оптических переходов из подзон тяжелых и легких дырок
- •3.4. Резонансное отражение и поглощение света в структурах с квантовыми ямами
- •3.5. Вторичное свечение гетероструктур
- •3.6. Квантовые микрорезонаторы
- •3.7. Заключение
- •Список литературы
- •4. Оптика квантовых точек
- •4.1. Введение
- •4.1.1. Состояния размерного квантования электронных и фононных возбуждений квантовых точек
- •4.1.2. Электрон-фононное взаимодействие в квантовых точках
- •4.1.3. Динамика электронных возбуждений квантовой точки
- •4.2. Оптические методы исследования квантовых точек
- •4.2.1. Изучение энергетической структуры электронных возбуждений
- •4.2.3. Исследование динамики элементарных возбуждений квантовых точек
- •4.2.4. Оптическая спектроскопия одной квантовой точки
- •4.3. Применение квантовых точек
- •4.3.1. Лазеры на квантовых точках для волоконной связи
- •4.3.2. Квантовые точки в биологии и медицине
- •Список литературы
- •5. Оптические резонансные свойства металлических наночастиц
- •5.1. Введение
- •5.2. Резонансы Ми отдельных металлических наночастиц
- •5.2.1. Эффект размера
- •5.2.2. Эффекты формы
- •5.3. Действие окружения на резонансы металлических наночастиц
- •5.3.1. Электродинамические эффекты
- •5.3.2. Контактные эффекты
- •5.4. Нелинейные оптические свойства металлических наночастиц
- •5.4.1. Генерация высших гармоник
- •5.4.2. Оптические комбинационные процессы
- •5.5. Неоднородные системы металлических наночастиц
- •5.5.1. Структурные параметры неоднородных систем
- •5.5.2. Измерение релаксационных параметров индивидуальных резонансов в неоднородных системах
- •5.6. Применения металлических наночастиц, связанные с их оптическими свойствами
- •5.7. Заключение
- •Список литературы
4. Оптика квантовых точек |
247 |
ния с участием оптического фонона к такой системе позволило определить, что ширина основного экситонного перехода ~ 2 = 6:3 ± 1:5 мкэВ.
4.2.4. Оптическая спектроскопия одной квантовой точки
Как видно из предыдущего параграфа, ряд методов оптической спектроскопии позволяет получать информацию о спектральных параметрах переходов и динамике возбуждений в индивидуальной квантовой точке из анализа спектров неоднородно уширенного ансамбля квантовых точек. Однако эта информация все же не является прямой и в ряде случаев может быть оспорена, поскольку эти методы используют ряд приближений, которые не всегда реализуются в исследуемых ансамблях. Поэтому вполне логичным является интерес к исследованию одиночной квантовой точки. Развитие высокочувствительных приемников оптического излучения, например структур с переносом заряда (ПЗС-матриц) и лавинных диодов, в сочетании с оптической микроскопией с дифракционно-ограниченным пространственным разрешением (200–500 нм) позволило решить эту проблему и получить новые данные о сверхтонкой структуре электронного спектра одиночной квантовой точки, как присущей ей самой, так и индуцированной внешними факторами, такими как световое поле, постоянные электрические и магнитные поля, наличие анизотропных напряжений и т.п.
Существуют два основных способа селекции одиночной квантовой точки из приготовленного ансамбля. В первом из них используется образец с малой поверхностной плотностью квантовых точек так, чтобы в области перетяжки возбуждающего излучения находилась одна или несколько квантовых точек. Этого сравнительно легко добиться в случае коллоидных нанокристаллов разных размеров, синтезируемых в растворах [127], которые далее в необходимых концентрациях внедряются в полимерные пленки или другие матрицы, допускающие фиксацию положения точек и проведение низкотемпературных экспериментов. В случае квантовых точек, выращенных в полупроводниковых гетероструктурах, получить образцы с малой поверхностной плотностью квантовых точек и с различными размерами достаточно трудно. Как правило, чем меньше поверхностная плотность, тем больше размер квантовой точки. В этих системах в совокупности с минимально возможной плотностью квантовых точек применяют технику приготовления меза-структур, в которых для возбуждающего излучения становятся доступными только считанное количество квантовых точек или всего одна квантовая точка [128]. Довольно экзотический способ использован при исследовании одиночных квантовых точек, создаваемых флуктуациями толщины сверхтонкого слоя (квантовой ямы) GaAs [123]. Здесь на поверхность слоя наносилось небольшое количество полимерных наносфер с диаметром от 50 до 500 нм, после чего структура покрывалась тонким слоем алюминия. Оказалось, что наносферы могут быть легко удалены с металлизированной поверхности, при этом остаются открытыми участки слоя с квантовой точкой, доступные для возбуждения светом.
248 А.В. Федоров, А.В. Баранов
Ниже будет видно, однако, что такую технику надо применять с осторожностью, поскольку некоторые параметры квантовой точки могут зависеть от размера меза-структур.
Резонансная фотолюминесценция
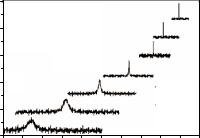
Одной из первых прямых демонстраций “атомоподобной” электронной структуры квантовых точек явилась работа группы исследователей из Массачусетского технологического института (США) [127]. В этой работе были получены низкотемпературные (10 К) спектры резонансной фотолюминесценции одиночных коллоидных нанокристаллов на основе CdSe, внедренных в 50-нанометровый слой полиметилметакрилата. Нанокристаллы со средним диаметром 3.9, 4.5 и 5.0 нм были приготовлены методом высокотемпературного металлоорганического синтеза в органическом растворителе и далее внедрены в полимерную матрицу в концентрации, обеспечивающей малую поверхностную плотность (менее одной квантовой точки на квадратный микрон). Для возбуждения и регистрации фотолюминесценции использовался оптический микроскоп, сопряженный со спектрометром, оборудованным охлаждаемым жидким азотом ПЗС-приемником. Диаметр освещаемой объективом области образца составлял 32 мкм, однако оптическая схема позволяла выбирать для записи спектров ФЛ различные одиночные квантовые точки. На рис. 4.26а показаны типичный спектр резонансной фотолюминесценции обычного образца, содержащего большое число CdSe квантовых точек (средний диаметр точек около 4.5 нм), и спектр одной квантовой точки из этого ансамбля. В обоих спектрах легко различима структура, соответствующая LO фонону CdSe. Уже здесь видно, что спектральная ширина линии фотолюминесценции одной квантовой точки на порядок меньше, чем для ансамбля точек. В правой части рисунка показано, как полоса фотолюминесценции ансамбля квантовых точек формируется из более узких полос, соответствующим одиночным квантовым точкам, входящим в ансамбль.
Оказалось, что наблюдаемые ширины линий одиночных квантовых точек определяются так называемым процессом спектральной диффузии: обратимыми многократными смещениями положения спектральной линии за время измерения (несколько минут) из-за ионизации квантовых точек и захвата носителей окружающей матрицей. Снижение интенсивности возбуждающего излучения и времени регистрации сигналов позволили авторам уменьшить влияние этого эффекта и продемонстрировать, что реальные ширины линий фотолюминесценции одиночной квантовой точки могут быть меньше спектрального разрешения используемой аппаратуры (менее 120 мкм) (рис. 4.27).
Таким образом, атомоподобная структура электронных состояний квантовых точек была продемонстрирована для наиболее очевидного типа квазинульмерных квантовых наноструктур. Появились реальные возможности экспериментального исследования процессов, определяющих динамику элек-

4. Оптика квантовых точек |
249 |
(а)
10 К
25.6 мэВ
13мэВ
1.26 мэВ
(б)
10 К
Рис. 4.26. а – сопоставление спектров резонансной фотолюминесценции обычного образца, содержащего большое число квантовых точек CdSe, и одной квантовой точки из этого ансамбля (диаметр точек около 4.5 нм). Легко различима структура, соответствующая LO фонону CdSe. Указаны HWHM линий резонансной фотолюминесценции. б
– иллюстрация формирования спектра фотолюминесценции ансамбля квантовых точек. Спектр ансамбля квантовых точек (средний диаметр – 3.9 нм) и набор спектров одиночных квантовых точек из этого ансамбля. Спектры получены при температуре 10 К [127].
Интенсивность
10 K
120 мкэВ
2.192 2.196
Энергия, эВ
Рис. 4.27. Спектр люминесценции одиночной квантовой точки CdSe с минимальной из измеренных шириной линии резонансной фотолюминесценции, полученный при малой мощности возбуждающего излучения. В этом эксперименте ширина линии ограничена спектральным разрешением, поэтому реальная ширина меньше 120 мкм [127].
250 А.В. Федоров, А.В. Баранов
тронных возбуждений в таких структурах, путем спектрального и временного анализа фотолюминесценции одиночной квантовой точки.
Особенно важна информация об этих процессах для квантовых точек, фабрикуемых в полупроводниковых гетероструктурах, совместимых с имеющимися эпитаксиальными технологиями изготовления полупроводниковых устройств наноэлектроники. В частности, одним из рассматриваемых перспективных областей применения квантовых точек является их использование в качестве элементов квантовых компьютеров и криптографов [132]. Основными элементами таких устройств являются двухуровневые квантовые биты (quantum bits, Q-bits), которые хранят квантовую информацию в форме линейной суперпозиции двух состояний. Атомоподобные электронные состояния квантовых точек рассматриваются как перспективные для таких элементов. Основным параметром Q-bits является время сохранения когерентности состояний, поскольку оно определяет времена хранения информации и скорость выполнения операций. Поэтому информация о физических процессах (важнейшим из которых является электрон-фононное взаимодействие), приводящих к сбою когерентности электронных возбуждений в квантовых точках, весьма важна. Поскольку те же процессы определяют однородную спектральную ширину линии соответствующего оптического перехода, то эта информация может быть получена из анализа температурной зависимости ширины линии фотолюминесценции одиночной квантовой точки.
В первых работах [99, 121, 133–135] сообщалось, что низкотемпературные значения времен дефазировки T2 = 2−1 фундаментального перехода, полученные из экспериментов по фотолюминесценции одиночной квантовой точки, не превышают 50 пс. Этот результат сильно ограничивал использование квантовых точек для хранения квантовой информации. Поскольку скорость полной дефазировки 2 = 1=2 + pd определяется скоростью релаксации населенности 1 и скоростью чистой дефазировки оптического перехода pd, именно большой вклад чистой дефазировки в 2 может отвечать за достаточно короткие времена T2 в исследуемых системах. Основной физической причиной этого является связь электронных возбуждений квантовой точки с ее собственными фононами и фононами окружения. Интерес к этой проблеме возрос снова после того, как две исследовательские группы сообщили о наблюдении в экспериментах по четырехволновому смешению времени низкотемпературной дефазировки T2 в несколько сотен пикосекунд [98, 99]. В работах [98, 99] различия результатов измерения скоростей дефазировки методами четырехволнового смешения и спектроскопии фотолюминесценции одиночной квантовой точки объяснялись в основном эффектом спектральной диффузии. Однако это объяснение было опровергнуто работой [128], в которой T2 = 730 пс было получено в фотолюминесцентных экспериментах с одиночной квантовой точкой. Использование спектральной аппаратуры с высоким разрешением, охлаждаемого жидким азотом ПЗС-приемника и техники литографического изготовления меза-структур для изоляции одиночной квантовой точки позволило авторам этой работы провести прямые измерения
4. Оптика квантовых точек |
251 |
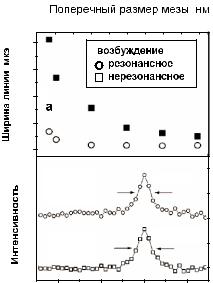
однородной ширины линии излучения, соответствующей распаду основного состояния экситона в самоорганизованных квантовых точках In0:6Ga0:4As, выращенных на подложке GaAs в диапазоне температур от 2 до 300 К. Спектральная ширина аппаратной функции используемого спектрометра составляла 2 мкэВ, поэтому использование процедуры деконволюции позволяло уверенно определять форму линий фотолюминесценции с шириной более 0.5 мкэВ. На рис. 4.28 приведен представительный набор спектров фотолюминесценции одной из исследуемых квантовых точек для ряда температур.
Интенсивность ФЛ
T = 2K
T = 77K
T = 100K
T = 150K
T = 200K
T = 250K
T = 300K
1.201.22 1.24 1.26 1.28
Энергия, эВ
Рис. 4.28. Спектры фотолюминесценции одной квантовой точки In0:6Ga0:4As/GaAs в диапазоне температур от 2 до 300 К [128].
В этой работе были получены важные сведения об ограничениях использования меза-структур для селекции одиночных квантовых точек, которые, по-видимому, не позволяли ранее получать столь узкие линии резонансной люминесценции, присущие одиночным квантовым точкам в гетероструктурах. Измерения ширины линии фотолюминесценции, проведенные при температуре 2 К, для мез разного размера, показали резкое уширение линий с уменьшением размера меза-структуры. В верхней части рис. 4.29 приведены эти зависимости для двух типов возбуждения фотолюминесценции квантовых точек: нерезонансного (через возбуждение электрон-дырочных пар GaAs буферных слоев) и резонансного (прямое возбуждение высокоэнергетических состояний квантовой точки). Легко видеть, что выбор меза-структуры слишком малого размера приводит к уширению линии фотолюминесценции на один-два порядка, по-видимому, из-за взаимодействия электронной подсистемы квантовых точек с материалом покрытия, используемым для приготовления меза-структур (обычно это металл). Физическая природа взаимодействия в настоящее время не совсем ясна. В частности, это может быть взаимодействие с плазмонами металлической пленки, аналогичное рассмотренным ранее в этой главе. В нижней части рис. 4.29 приведены примеры спектров линии фотолюминесценции двух разных одиночных квантовых точек, изме-
252 А.В. Федоров, А.В. Баранов
|
|
|
|
, |
100 |
200 |
300 |
400 |
500 |
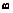 160
160
, |
120 |
|
|
|
|
|
|
|
80
( )
40
0
(b)
3.41 
 = 1.3146
= 1.3146 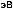
3.56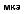
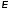 = 1.2852
= 1.2852 
-0.02 -0.01 0.00 0.01

 ,
, 
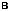
Рис. 4.29. а – ширина линии фотолюминесценции одиночной квантовой точки In0:6Ga0:4As, измеренная при = 2 К, как функция поперечного размера мезаструктуры, содержащей квантовую точку. б – спектры фотолюминесценции двух разных одиночных квантовых точек, полученные при 2К для размера мез 400 нм. Для простоты сопоставления линий энергии, соответствующие центрам линий, были вычтены. Их величины показаны на каждом из спектров [128].
ренных при больших пространственных размерах мез (400 нм), когда ширина спектральной линии не зависит от их размера. Спектры демонстрируют узкие линии лоренцева типа с шириной 3.4±0:4 мкэВ. Деконволюция линий с аппаратной функцией спектральной аппаратуры с шириной 2 мкэВ позволила получить истинное значение 2~ 2 = 1:8 ± 0:4 мкэВ (T2 730 пс) при 2 К. Температурные измерения показали, что однородная ширина линии линейно растет с температурой до 60 К: 2 = 20 + acT , где 20 соответствует нулевой температуре, а ~ ac = 0:5 мкэВ обусловлена рассеянием электронных возбуждений на акустических фононах гетероструктуры. Простая экстраполяция к нулевой температуре показывает, что величина ~ 20 явно меньше 1.5 мкэВ. Это значение соответствует времени полной дефазировки в 900 пс. Слабое взаимодействие с акустическими фононами ( ac, по крайней мере, в 5 раз меньше, чем для квантовых ям [136]) и то обстоятельство, что T2, в основном определяется временем жизни экситона (прямые временные´ измерения показали, что время затухания фотолюминесценции этих точек равно при-
4. Оптика квантовых точек |
253 |
мерно 1 нс) подтверждают перспективность использования квантовых точек в системах обработки квантовой информации.
Когерентный контроль фундаментального перехода в одиночной квантовой точке
Различия в данных о динамике электронных возбуждений, получаемые при изучении ансамблей квантовых точек и одиночных квантовых точек, формируемых в гетероструктурах, поставили задачу привлечения новых дополнительных методов исследования. Одним из таких перспективных направлений является применение техники когерентного контроля спонтанного вторичного свечения, описанной в предыдущем разделе этой главы, к исследованию одиночной квантовой точки. Первое сообщение об экспериментальной реализации когерентного контроля оптических переходов в одиночной квантовой точке появилось в 1998 году [123]. Квантовые точки, исследованные в этой работе, формировались из-за флуктуаций толщины 4-нанометрового слоя GaAs, находящегося между 25-нанометровыми барьерами Al0:3Ga0:7As. На слои наносилась пленка Al с толщиной 100 нм, где были сформированы отверстия с диаметром 500 нм, через которые возбуждалась одиночная квантовая точка. На рис. 4.30 показана энергетическая экситонная структура этих
Интенсивность, отн. ед.
Е
Е
Е
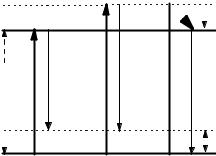
Рис. 4.30. Кривая затухания интегрированного во времени сигнала резонансной люминесценции одиночной квантовой точки GaAs при увеличении времени задержки между двумя сфазированными лазерными импульсами с энергией фотонов, резонансной переходам в экситонные состояния E1X и E1Y [123]. На вставке – энергетическая структура экситонных состояний в индуцированной флуктуациями толщины одиночной квантовой точки GaAs. Указаны основное состояние экситона E0 и следующее возбужденное состояние, расщепленное на два: E1X и E1Y . Показана схема оптических переходов, обсуждаемых в тексте.
254 А.В. Федоров, А.В. Баранов
одиночных точек, установленная в предварительных фотолюминесцентных экспериментах. Помимо основного экситонного состояния E0, было установлено наличие двух возбужденных состояний, одно из которых E1 было расщеплено на два E1X и E1Y c однородными ширинами 2~ 2 17 мкэВ, что соответствует T2 39 пс. В то же время спектральное разрешение используемой аппаратуры не позволяло определить ширину фундаментального перехода в фотолюминесцентных экспериментах. Этого не удалось сделать и при использовании техники когерентного контроля соответствующей резонансной люминесценции. Действительно, в этом случае энергия детектируемых фотонов резонансной люминесценции совпадает с энергией фотонов возбуждающего света и наличие интенсивного рассеяния возбуждающего излучения от исследуемой гетероструктуры не оставляло надежд на выделение полезного сигнала. В результате оказалось возможным реализовать когерентный контроль фундаментального перехода только при резонансном возбуждении светом E1X- и E1Y -состояний квантовой точки, энергия которых была на 2.6 мэВ выше E0. Основное состояние экситона заселялось за счет переходов с высокоэнергетических состояний, а анализируемая люминесценция могла быть селектирована спектрально. Таким образом, в этой работе был реализован когерентный контроль термализованной люминесценции, теория которой для ансамбля квантовых точек приведена в предыдущем разделе этой главы, применительно к одиночной квантовой точке. В результате эксперимента была получена кривая затухания интенсивности интегрированной во времени резонансной люминесценции квантовых точек с характерным временем около 40 пс (рис. 4.30), что практически совпадает с T2 = −1 39 пс, определенной из спектрального анализа однородной ширины линий оптических переходов из состояний E1X и E1Y . Несмотря на то что в цитируемой работе не удалось определить характерные времена релаксации фундаментального перехода, ее результаты продемонстрировали работоспособность этого метода и совпадение полученных данных с результатами традиционных спектральных экспериментов.
Дальнейшие работы в этом направлении [137] показали, что для исследования динамики фундаментального перехода в одиночной квантовой точке может служить когерентный контроль спонтанного вторичного свечения с участием оптических фононов. Проинтегрированный по времени сигнал вторичного свечения с участием оптических фононов от одиночной квантовой точки (схема возможных переходов показана на рис. 4.31), возбуждаемой парой сфазированных импульсов с несущей частотой !L и взаимной задержкой, может быть представлен следующим образом:
|
V |
∞ |
∞ |
|
|
|
I( ) = |
Z d!R!R3 G(!R − !D) |
Z |
dtW!R (t); |
(4.95) |
||
|
||||||
(2 c)3 |
0−∞
где W!R (t) – вероятность испускания фотона !R с участием оптического фонона, G(!R − !D) – спектральная функция регистрирующей системы, !D –
4. Оптика квантовых точек |
255 |
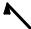
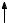 Ω
Ω
ωe |
|
ωL ωR ωL ωR ωL |
ωR |
|
|
||||
|
||||
|
||||
|
||||
|
|
|
Ω |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
|
|
a b c
Рис. 4.31. Схема возможных переходов, определяющих спонтанное вторичное свечение с участием оптических фононов. !e, !L, !R и – частоты экситонного перехода, падающего света, испускаемого света и оптического фонона. a – случай входного резонанса. b и c – случаи выходного резонанса. Процессы a и b cоответствуют резонансному рассеянию и люминесценции. Процесс c – так называемая термализованная люминесценция, состоящая из генерации экситона с участием фонона, распада фонона из-за ангармоничности и испускания фотона.
частота детектирования и V – нормировочный объем. Вводя плотность состояний оптических фононов g( ), W!R (t) можно выразить через вероятность испускания фотона с рождением или аннигиляцией оптического фонона с частотой :
( ) |
(t): |
(4.96) |
W!R (t) = Z d g( )W!R |
В дальнейшем ограничимся низкотемпературным пределом, когда температура T << ~=kB (kB – постоянная Больцмана), и будем рассматривать только стоксову компоненту вторичного свечения. Предположим, что !L близка к частоте экситонного перехода !e, т.е. реализуется входной резонанс (рис. 4.31, a). Тогда при условии, что спектральная ширина импульсов удовлетворяет стандартным для схемы когерентного контроля неравенствам << <<E; ~ ( E – энергетическая щель между резонансным и ближайшим к нему экситонным состоянием, ( = 1; 2; ph) – релаксационные константы), легко получить следующее выражение для величины I( ):
I( ) = |
16 2 (!D) 1 + e− 2 cos !e |
; |
(4.97) |
||
1 |
|
( 2L + 2)2 |
|||
где |
|
|
|
||
(!D) = Z d g( ) ( )G( D ); |
|
(4.98) |
|||
256 А.В. Федоров, А.В. Баранов
|
E2 !3 |
|
V(R) |
2 |
|
V |
(L) |
2 |
| |
V |
| |
2 |
|
|
||||
( ) = |
|
|
|
|
|
|
|
|
|
|
|
|
; |
(4.99) |
||||
|
|
|
|
5 |
|
2 |
|
|
|
|
3 |
|
|
|
|
|||
|
|
|
"~ |
(4 |
c) |
|
|
|
|
|
|
|||||||
|
L |
R |
|
|
gi |
|
|
|
|
ig |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D = !e − !D − , L = !e − !L,( ) |
R =( !)*e − !R − , = R − L, " – |
|||||||||||||||||
диэлектрическая проницаемость, Vig |
|
= Vgi |
|
= i| (−er)ˆe |g ( = L; R), er – |
||||||||||||||
оператор дипольного момента, eˆL и eˆR – векторы поляризации, EL – напряженность электрического поля, V = i| V (r) |i – матричный элемент электронфононной связи, |g и |i – основное и возбужденное электронные состояния. При выводе (4.97) считалось, что полоса пропускания детектирующей системы D >> 2 + ph=2.
Этот результат крайне важен для определения полной скорости дефазировки резонансного оптического перехода. В самом деле, недостаточно хорошо известные параметры системы g( ), ( ) и G( D ) факторизуются и входят в выражение (4.97), описывающее сигнал как постоянный множитель. Отсюда следует, что форма измеряемого сигнала не зависит от природы оптических фононов, участвующих в процессе вторичного свечения, и не зависит от типа электрон-фононной связи. Это могут быть собственные фононы квантовой точки и/или фононы барьеров и матрицы, связанные с электронной подсистемой квантовой точки через полярное взаимодействие и через деформационный потенциал. Во всех этих случаях сигнал является одиночной интерферограммой, осциллирующей на частоте электронного перехода !e. Огибающая функция интерферограммы exp(− 2 ) определяется только полной скоростью дефазировки 2. Важно отметить, что разделение сигнала на резонансное рассеяние и резонансную люминесценцию невозможно в принципе для широкополосного фильтра. Если неравенство D >> 2 + ph=2 нарушается, то упомянутая выше факторизация невозможна и определение 2 из экспериментально наблюдаемого затухания интерферограммы становиться более сложной задачей.
Известно, что сигнал вторичного свечения с участием оптических фононов может возникать также и при выходном резонансе (см. рис. 4.31, b и c): !L !e + . Можно показать, что в этом случае даже для широкополосного фильтра факторизация возможна лишь при специальных предположениях о плотности фононных состояний и/или о матричных элементах электронфононной связи. Спектральная ширина g( ) ( ) должна быть много меньше спектральной ширины лазерных импульсов. Физически это соответствует очень узкой плотности фононных состояний и/или острому пику в зависимости электрон-фононной связи от фононной частоты, т.е. случаю, когда система может рассматриваться в одномодовом приближении. Тогда анализируемый сигнал также является одиночной интерферограммой, осциллирующей на частоте !e + 0, где 0 – центральная частота функции g( ) ( ). Огибающая интерферограммы exp(− 2 − ph=2) определяется как скоростью дефазировки электронного перехода, так и обратным временем жизни фонона и, следовательно, для определения 2 нужны независимые данные о ph.
Проведенное выше рассмотрение подразумевает, что неоднородное уширение фундаментального перехода пренебрежимо мало для одиночной кван-
4. Оптика квантовых точек |
257 |
товой точки. Однако предполагалось, что расхождение между величинами ~ 2, измеренными для одиночной точки (несколько десятков микроэлектронвольт [99, 134, 135]) и для ансамбля точек (несколько микроэлектронвольт [98, 99]) возникает из-за неоднородного уширения перехода, обусловленного флуктуациями зарядового окружения (спектральная диффузия) [98, 99]. В результате ширины линий, получаемые методом фотолюминесцентной спектроскопии одиночной квантовой точки с длительным временем накопления сигналов, отражают это неоднородное уширение в то время, как спектроскопия четырехволнового смешения дает правильное значение 2, поскольку характерное время флуктуаций много больше, чем время между первым импульсом и сигналом эха. Это предполагает, что фундаментальный экситонный переход в одиночной квантовой точке неоднородно уширен и его исследование линейными оптическими методами не может дать надежную информацию о процессах дефазировки. Однако заранее неясно каков вклад флуктуаций в спектральную ширину перехода и как он зависит от условий возбуждения, параметров квантовой точки и ее окружения, а также конструкции исследуемого образца. Недавнее наблюдение экстремально узкой лоренцевой линии люминесценции (~ 2 = 0:9 мкэВ) в одиночной квантовой точке показало, что спектральной диффузии можно избежать, подходящим выбором размера мезы и резонансным возбуждением состояний квантовой точки. Эти условия полностью соответствуют схеме когерентного контроля. Тем не менее, рассмотрим сигнал когерентного контроля в условиях неоднородного уширения благодаря флуктуациям зарядового окружения. Поскольку верхний предел для ширины ! этого неоднородного уширения составляет несколько десятков микроэлектронвольт, оно может быть легко учтено в рассматриваемой модели. Для этого I( ) необходимо усреднить по некоторой функции распределения. Используя условие ! << ; D, получаем
I¯( ) = |
16 2 ¯(!D) |
|
1 + e− 2 F( ) cos !0 |
; |
|
(4.100) |
||
|
|
|
||||||
где F( ) – фурье–образ |
1 |
|
|
( ¯2L + 2)2 |
¯ |
|
¯ |
получают- |
функции |
распределения, |
(!D) |
и L |
|||||
ся из (!D) и L путем замены !e на среднюю частоту электронного перехода !0. В случае гауссовой функции распределения F(!e − !0) = (!)−1=2 exp [−(!e − !0)2= !2] огибающая функция интерферограммы будет равна K( ) = exp (− 2 − !2 2=4). На рис. 4.32a представлена функция K( ), вычисленная для различных отношений 2= !. Форма кривых не зависит от абсолютных величин 2 и !. На рисунке их величины были выбраны так, чтобы полуширина фотолюминесцентной линии одиночной квантовой точки на полувысоте сохранялась постоянной (21:25 мкэВ) в соответствии с работой [99]. Можно видеть, что присутствие неоднородного уширения можно легко обнаружить. Количественные данные о 2 и ! могут быть получены простой подгоночной процедурой. Вообще говоря, те же данные можно найти, анализируя спектральную форму линии люминесценции. Однако анализ формы включает две процедуры: деконволюцию спектральной функции
