
- •1. Фотонные кристаллы
- •1.1. Концепция
- •1.1.1. Электроны в кристаллических структурах
- •1.1.2. Электромагнитные волны в кристаллических структурах
- •1.1.3. Фотонное твердое тело: распространение и локализация электромагнитных волн в условиях сильного многократного рассеяния
- •1.2. Синтез и свойства фотонных кристаллов
- •1.2.1. Фотонные кристаллы в природе
- •1.2.2. Одномерные периодические структуры
- •1.2.3. Двумерные периодические структуры
- •1.2.4. Трехмерные периодические структуры
- •1.3. Испускание и рассеяние излучения в фотонных кристаллах: роль плотности фотонных состояний
- •1.3.1. Интегральная и локальная плотности состояний
- •1.3.2. Спонтанное испускание фотонов
- •1.3.3. Тепловое излучение
- •1.3.4. Комбинационное рассеяние
- •1.3.5. Резонансное (релеевское) рассеяние
- •1.4. Заключение
- •Список литературы
- •2. Оптическое излучение в линейных и нелинейных периодических структурах
- •2.1. Введение
- •2.2.1. Квазиоптическое приближение
- •2.2.2. Линзовые волноводы и лазерные резонаторы
- •2.2.4. Мелкомасштабная самофокусировка в периодических системах
- •2.2.5. Квазисинхронное параметрическое взаимодействие
- •2.3. Одномодовый световод с брэгговской решеткой
- •2.3.1. Двунаправленное распространение излучения
- •2.3.2. Брэгговские солитоны
- •2.3.3. Оптическая бистабильность и переключение
- •2.3.4. Полупроводниковые микрорезонаторы
- •2.4. Связанные световоды
- •2.5. Двумерные фотонные кристаллы
- •2.5.1. Неидеальные фотонные кристаллы
- •2.5.2. Нелинейные двумерные фотонные кристаллы
- •2.6. Заключение
- •Список литературы
- •3. Оптика квантовых ям и сверхрешеток
- •3.1. Классификация гетероструктур
- •3.2. Размерное квантование электронных состояний
- •3.3. Правила отбора при оптических переходах
- •3.3.1. Междузонные и внутризонные оптические переходы между подзонами размерного квантования
- •3.3.2. Поляризационные свойства оптических переходов из подзон тяжелых и легких дырок
- •3.4. Резонансное отражение и поглощение света в структурах с квантовыми ямами
- •3.5. Вторичное свечение гетероструктур
- •3.6. Квантовые микрорезонаторы
- •3.7. Заключение
- •Список литературы
- •4. Оптика квантовых точек
- •4.1. Введение
- •4.1.1. Состояния размерного квантования электронных и фононных возбуждений квантовых точек
- •4.1.2. Электрон-фононное взаимодействие в квантовых точках
- •4.1.3. Динамика электронных возбуждений квантовой точки
- •4.2. Оптические методы исследования квантовых точек
- •4.2.1. Изучение энергетической структуры электронных возбуждений
- •4.2.3. Исследование динамики элементарных возбуждений квантовых точек
- •4.2.4. Оптическая спектроскопия одной квантовой точки
- •4.3. Применение квантовых точек
- •4.3.1. Лазеры на квантовых точках для волоконной связи
- •4.3.2. Квантовые точки в биологии и медицине
- •Список литературы
- •5. Оптические резонансные свойства металлических наночастиц
- •5.1. Введение
- •5.2. Резонансы Ми отдельных металлических наночастиц
- •5.2.1. Эффект размера
- •5.2.2. Эффекты формы
- •5.3. Действие окружения на резонансы металлических наночастиц
- •5.3.1. Электродинамические эффекты
- •5.3.2. Контактные эффекты
- •5.4. Нелинейные оптические свойства металлических наночастиц
- •5.4.1. Генерация высших гармоник
- •5.4.2. Оптические комбинационные процессы
- •5.5. Неоднородные системы металлических наночастиц
- •5.5.1. Структурные параметры неоднородных систем
- •5.5.2. Измерение релаксационных параметров индивидуальных резонансов в неоднородных системах
- •5.6. Применения металлических наночастиц, связанные с их оптическими свойствами
- •5.7. Заключение
- •Список литературы
234 А.В. Федоров, А.В. Баранов
состояния стремится к асимптотическому значению E111 + ~ 211 гораздо медленнее, чем в случае малых 2~!−Eex. Такое поведение связано с сильной размерной зависимостью экситон-фононного взаимодействия. Эта зависимость приводит к тому, что для квантовых точек достаточно малых размеров влияние колебательного резонанса на энергетический спектр существенно даже вдали от колебательного резонанса.
4.2.3.Исследование динамики элементарных возбуждений квантовых точек
В этом параграфе мы остановимся на динамике электронных возбуждений (экситоны, электроны и дырки) квантовой точки. Она определяется двумя процессами: изменением энергии возбуждения (переходом в другое энергетическое состояние), характеризуемом временем распада населенности (временем жизни) исходного состояния, T1, и дефазировкой волновой функции состояния без изменения его энергии, характеризуемой временем “чистой” дефазировки, Tpd, в результате различного типа взаимодействий. Информация об этих процессах и механизмах, приводящих к ним, может быть получена из спектрального и временного анализа оптических переходов между исследуемым состоянием возбуждения и основным. Это оказывается возможным, поскольку в большинстве случаев основное состояние можно считать стационарным. Соответствующая однородно уширенная спектральная линия имеет полуширину на половине высоты (HWHM - half width on half of maximum)
2 = 1=2 + pd = T2−1 = ((2T1)−1 + Tpd−1), где 1 и pd - скорости релаксации населенности и чистой дефазировки соответственно, а T2 - время полной
дефазировки. Время жизни T1 определяется радиационным распадом состояния, а также безызлучательными переходами в другие возможные состояния
врезультате неупругих (с изменением энергии) столкновений с другими возбуждениями, например переходами с рождением или уничтожением фононов, индуцированными электрон-фононным взаимодействием. Tpd определяется упругими столкновениями, в результате которых одновременно рождается и уничтожается виртуальное возбуждение того же или другого типа, например фонон.
Таким образом, знание двух характерных времен из этого набора полностью характеризует динамику возбуждения. Конкретные механизмы, определяющие динамику, могут быть найдены из их зависимостей от различных внешних параметров. В частности, сравнительный анализ температурных зависимостей T1 и T2 часто используется для анализа процессов дефазировки
вквантовых точках.
Простейшим случаем является двухуровневая система с временем жизни, определяемым радиационным распадом и чистой дефазировкой, связанной с упругим рассеянием на фононах. При температурах о нескольких десятков градусов Кельвина вклад оптических фононов пренебрежим из-за низкой плотности фононов [97]. Тогда процесс чистой дефазировки определяется
4. Оптика квантовых точек |
235 |
упругими столкновениями с акустическими фононами, имеющими непрерывный спектр, что приводит к резкой зависимости от температуры Tpd T −7 скорости чистой дефазировки и, естественно, той же температурной зависимости T2. Наличие тонкой экситонной структуры с характерным энергетическим зазором , что обычно для большинства систем квантовых точек, дает совершенно другую температурную зависимость. Возможность осуществления реальных переходов между энергетическими состояниями с рождением или поглощением акустических фононов с энергией приводит к возникновению дополнительного вклада в T2, связанного с температурной зависимостью как T1, так и Tpd. В низкотемпературном пределе (" > kBT ), T1 и Tpd будут пропорциональны T −1 и T −2 соответственно. В противоположном случае T1 не зависит от температуры для переходов с испусканием фононов и T1 exp(=kBT ) для переходов с поглощением фононов. Именно этот процесс отвечает за наблюдавшуюся в низкотемпературных (5–40 К) экспериментах [98, 99] линейную температурную зависимость скорости дефазировки в квантовых точках InxGa1−xAs. Отсюда следует, что процесс дефазировки в этих системах при низкой температуре в основном определяется T1. В то же время физика чистой дефазировки в квантовых точках остается не совсем ясной. В частности, предсказываемая нелинейная зависимость Tpd (T 2 + bT 7)−1 до сих пор надежно не наблюдалась в системах квантовых точек, хотя вклад чистой дефазировки в динамику фундаментального экситонного перехода в квантовых точках InxGa1−xAs сопоставим с вкладом релаксации населенности T1.
Обычно исследуемые реальные образцы содержат ансамбль квантовых точек, поэтому спектр их оптических переходов неоднородно уширен из-за неодинаковых размеров и формы квантовых точек, различного локального окружения, а также несколько различного состава. В результате, формы линий резонансной люминесценции и соответствующей полосы поглощения становятся несимметричными, а их спектральные ширины даже при температуре 2 К составляют от единиц до десятков миллиэлектронвольт [11]. Поэтому экспериментальные измерения T1 и T2 для одной квантовой точки представляют не простую задачу.
Для измерения T1 обычно используют прямые измерения кинетики затухания резонансной люминесценции при возбуждении носителей в квантовых точках световым импульсом с длительностью, существенно меньшей T1, и энергией фотонов, достаточной для возбуждения высокоэнергетических состояний квантовых точек или состояний барьерного слоя (подложки). В этом случае нижайшее возбужденное состояние квантовой точки заселяется за счет быстрой термической релаксации носителей. Искомые времена затухания, как правило, лежащие в диапазоне 10 пс – 10 нс, могут быть прямо измерены с помощью стрик-камер, техники счета фотонов в комбинации с методом задержанных совпадений или техники ап-конверсии [100]. Такие измерения, однако, дают величины T1, усредненные по ансамблю квантовых точек, и к их использованию надо подходить с осторожностью.
236 А.В. Федоров, А.В. Баранов
Для получения информации о T2 в ансамблях квантовых точек используют как спектральные, так и временные´ методы, развитые при изучении неоднородно уширенных переходов молекулярных ансамблей [101]. Первый из них – метод выжигания стационарных провалов в спектре поглощения квантовых точек [102], который позволяет измерять однородную ширину спектрального перехода одной квантовой точки из исследуемого ансамбля, а второй – техника четырехволнового смешения и фотонного эха [98, 99, 103, 106]
– позволяет определять время полной дефазировки T2, соответствующей всему ансамблю, возбуждаемому импульсом. Очевидно, что они должны давать одни и те же значения в случае одинаковой электронной динамики квантовых точек в ансамбле. Остановимся кратко на результатах, полученных этими методами.
Спектроскопия выжигания стационарных провалов
Техника выжигания стационарных провалов является одним из методов размерно-селективной спектроскопии квантовых точек. Здесь неоднородно уширенный ансамбль освещается спектрально узким излучением, ширина которого много меньше ожидаемой спектральной ширины исследуемого перехода, а энергия фотонов резонансна фундаментальному переходу какой-либо из квантовых точек, входящих в ансамбль. В результате происходит селективное резонансное возбуждение подансамбля точек с одинаковыми параметрами в пределах однородной ширины перехода. Меняя длину волны возбуждения, можно последовательно возбуждать все квантовые точки. Непременным условием выжигания стационарных провалов является наличие механизмов,
восновном связанных с наличием матрицы (ионизация при уходе носителей
вматрицу, фотохимическая реакция и т. п.), которые приводят к стационарному изменению населенности основного состояния точек, резонансно возбуждаемых светом. При этом соответствующая полоса поглощения исчезает из спектра поглощения ансамбля или заметно уменьшается по интенсивности. Если теперь записать спектр поглощения ансамбля, используя слабое
зондирующее излучение, то в контуре поглощения будет наблюдаться спек-
тральный провал с HWHM равной 2 2 = 2T2−1. Таким образом, провал имеет ширину в два раза больше однородной ширины оптического перехода. Это происходит из-за того, что такая методика использует процесс поглощения дважды – при выжигании провала и при его детектировании. Для применения этого метода необходимо, чтобы была возможность прямого измерения спектров поглощения, что возможно только для квантовых точек, внедренных
вдиэлектрические матрицы.
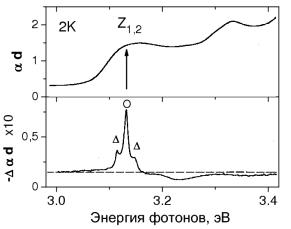
Такие измерения были неоднократно проведены для фундаментального перехода квантовых точек в режиме как сильного (CdSe и CuI), так и слабого (CuCl и CuBr) конфайнмента (см., например, [104, 105]). На рис. 4.22 показан пример спектра выжигания провалов в неоднородно уширенной полосе поглощения квантовых точек на основе CuI, находящихся в режиме сильного конфайнмента. В частности, в работе [104] для перехода 1S3=21Se в квантовых
4. Оптика квантовых точек |
237 |
(а)
CuI в стекле
R = 3.5 нм
(б)
Рис. 4.22. Выжигание провалов в квантовых точках CuI, внедренных в стеклянную матрицу, при 2 К. а – спектр поглощения исходного образца. Отмечена полоса, соответствующая неоднородно уширеному фундаментальному переходу экситона Z1;2. б
– изменения в спектре после облучения образца излучением узкополосного лазера с энергией фотонов 3.13 эВ. Кружком помечена линия резонансного перехода, треугольниками – линии переходов с участием акустических фононов [102].
точках CdSe/ZnS, внедренных в полимерную матрицу, спектр стационарных провалов был получен c использованием двух перестраиваемых диодных лазеров со спектральной шириной излучения 0.4 мкэВ. Спектр состоял их узкой линии резонансного перехода, перекрывающегося с более широкой линией, соответствующей переходу с участием акустических фононов. При температуре 2 К минимальная однородная ширина перехода 2~ 2 составляла 32 мкэВ. Ее зависимость от температуры была существенно нелинейной (при 10 К 2~ 2 = 670 мкэВ), показывая, что основной вклад в уширение вносит процесс чистой дефазировки, вызванной упругим рассеянием электронных возбуждений на акустических фононах. Этим же методом была измерена однородная ширина и ее температурная зависимость для фундаментального перехода Z3- экситона в квантовых точках на основе CuCl, выращенных в кристалле NaCl. При температуре 2 К ее однородная ширина оказалась равной 0.4 мэВ для точек с радиусом 3.5 нм. В отличие от CdSe-точек, ее зависимость от температуры была близка к линейной, показывая, что процесс дефазировки связан с рождением акустических фононов с энергией 2.2 мэВ.
Эксперименты по выжиганию провалов в ансамблях квантовых точек, внедренных в разные матрицы, показывают сильное влияние материала матрицы и способа внедрения точек на величину однородной ширины перехода и на ее температурную зависимость. Наличие такой зависимости понятно, поскольку в большинстве случаев именно взаимодействие квантовой точки и матрицы приводит к возможности выжигания долгоживущих провалов. Это обстоятельство можно использовать для изучения влияния матрицы на элек-
238 А.В. Федоров, А.В. Баранов
тронную динамику квантовых точек, однако, для понимания динамики возбуждений в самой квантовой точке такое влияние желательно минимизировать.
Четырехволновое смешение и фотонное эхо
При низких температурах однородные ширины спектральных переходов квантовой точки во многих случаях по величине близки к разрешению дифракционных спектрометров, что затрудняет их измерения. Поэтому для получения информации о T2 в неоднородно уширенных ансамблях квантовых точек широко используются нелинейные оптические методы нестационарной спектроскопии, например фотонное эхо [107]. Этот метод особенно подходит для изучения квантовых точек, выращенных в полупроводниковых гетероструктурах, где наличие подложки и буферных слоев делает невозможным измерение спектров поглощения точек.
Детальное описание реализации этого метода, который основан на зондировании пробным коротким импульсом зависимости интерференции поляризаций элементов ансамбля, созданной парой коротких возбуждающих световых импульсов, от времени задержки между ними, можно найти в [100]. Для реализации метода необходимо выполнение условий фазового синхронизма между волновыми векторами возбуждающих импульсов (k1 и k2), зондирующего импульса (k3), а также импульса фотонного эха (ke). Поэтому сигнал фотонного эха наблюдается только в определенном направлении, например ke = 2k2 − k1 при k3 = k2 или ke = k2 при k3 = k1. Если интенсивность второго возбуждающего импульса, задержанного относительно первого на t12, удовлетворяет определенным требованиям, то сигнал фотонного эха, генерируется еще через t12 и определяется макроскопической поляризацией всего ансамбля. Интенсивность сигнала уменьшается с временем задержки, причем по-разному для разных конфигураций эксперимента: exp (−4t12=T2) для ke = 2k2 −k1 и exp (−2t12=T2) для ke = k2. В обоих случаях появляется возможность измерения времени полной дефазировки в неоднородно уширенном ансамбле. Индуцированная интерференционная картина является, вообще говоря, динамической. Однако в некоторых случаях интерференция поляризаций приводит к формированию в исследуемом объеме образца квазистационарной интерференционной картины, связанной с движением населенностей. В этом случае говорят об аккумулированном фотонном эхе, сигнал которого на 2–3 порядка превышает сигнал обычного фотонного эха [102, 103, 106, 108]. Характерной особенностью аккумулированного фотонного эха является линейная зависимость его интенсивности от мощности возбуждающих импульсов. Очевидно, что эффект аккумулированного фотонного эха характерен для тех же ансамблей квантовых точек, где наблюдается выжигание стационарных провалов [102].
Этот метод измерения T2 был впервые продемонстрирован для ансамбля квантовых точек CuBr [109], а в работе [103] он был использован для исследования дефазировки Z3-экситона в сферических квантовых точках CuCl,

4. Оптика квантовых точек |
239 |
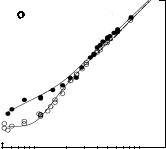
внедренных в стекло. Время релаксации когерентности T2 при температуре 2 К оказалось равным 130 пс, что соответствует ~ 2 10 мкэВ. Сравнение T2 с T1, измеренным в независимом эксперименте, показало, что T2 при 2 К в пределах ошибок эксперимента ( 10%) совпадает с 2T1. Это свидетельствует о том, что, как и в атомных системах, динамика экситона в исследуемых квантовых точках определяется в основном его энергетической релаксацией, а процессы чистой дефазировки весьма слабы. Обратно пропорциональная температурная зависимость T2 в области 2–50 К так же показала, что дефазировка связана, прежде всего, с неупругими процессами, влияющими на время релаксации населенности T1. В этих экспериментах было обнаружено, что T2 увеличивается с уменьшением мощности возбуждающих импульсов, поэтому значение T2 было получено при мощностях, минимально возможных для регистрации сигнала. Не исключено, однако, что реальные предельно длинные времена дефазировки Z3-экситона так и не были достигнуты. Модификация метода аккумулированного фотонного эха с использованием фазовомодуляционной техники [106] позволила существенно уменьшить мощности возбуждения (меньше одного фотона на точку) при сохранении чувствительности измерений. В результате были измерены времена полной дефазировки фундаментального перехода Z3-экситона в примерно одинаковых по размеру квантовых точках на основе CuCl, внедренных в стеклянную матрицу (CuCl/стекло) и в кристалл NaCl (CuCl/NaCl), при температурах до 0.7 К. На рис. 4.23 показаны примеры полученных кривых для разных температур. Использовалась геометрия эксперимента, в которой уменьшение интенсивно-
Сигнал фотонного эха
 CuCl/NaCl
CuCl/NaCl
 CuCl/стекло
CuCl/стекло
10-1 
2 K
10-3  4 K
4 K
10 K
0 200 400
Время задержки, t 12 , пс
Рис. 4.23. Зависимости сигналов фотонного эха квантовых точек CuCl от времени задержки между импульсами возбуждения, t12 для разных температур. Пустые и заполненные кружки – данные для CuCl/NaCl и CuCl/стекло соответственно. Сплошные линии – аппроксимация данных би-экспоненциальным распадом. Время затухания медленных компонент для кривых в направлении сверху вниз: 310, 117, 65, 55, 9.6 и 9.5 пс соответственно [106].
сти сигнала эха описывается выражением exp (−2t12=T2). Экспериментальные
240 А.В. Федоров, А.В. Баранов
зависимости хорошо описывались биэкспоненциальным распадом, в котором медленный компонент соответствовал распаду когерентности фундаментального перехода, а быстрый (10–30 пс) – переходу с участием оптического фонона. Видно, что при температуре 2 К времена дефазировки квантовых точек, внедренных в разные матрицы, существенно различаются. Для матрицы NaCl T2 = 620 пс, а для стекла T2 = 334 пс (~ 2 равно 1 и 1.9 мкэВ соответственно). В области 2–50 K наблюдался линейный рост 2 с повышением температуры, что демонстрирует преобладающий вклад в дефазировку энергетической релаксации экситона. Однако при температурах меньших 2 К для квантовых точек CuCl/NaCl эта зависимость становится существенно нелинейной (рис. 4.24), что свидетельствует о наличии дополнительных механизмов дефазировки, индуцированных окружением. Интересно сравнить данные о T2, полученные из экспериментов по фотонному эху, с временами T1, определен-
1000 |
CuCl/NaCl |
|
 CuCl/стекло
CuCl/стекло
мкэВ, |
100 |
|
|
||
2 |
10 |
|
γ |
|
|
2 |
|
|
|
|
1 |
1 |
10 |
Температура, К
Рис. 4.24. Зависимость однородной ширины Z3 экситона в CuCl квантовых точках, внедренных в кристаллическую (пустые кружки) и стеклянную (заполненные кружки) матрицы, от температуры [102].
ными в прямых измерениях времени затухания резонансной люминесценции квантовых точек при температуре 0.7 К. Для системы CuCl/NaCl T1 = 3:56 нс, что соответствует ~ 2 0.1 мкэВ. Величина 2 оказалась существенно меньше полученной из эксперимента по фотонному эху (0.5 мкэВ), показывая наличие быстрых процессов чистой дефазировки в квантовых точках CuCl
вкристаллической матрице. В то же время для квантовых точек в стекле T1 = 0:6 нс, а ~ 2 0:55 мкэВ очень близка к ее значению, измеренному
вэкспериментах по фотонному эху. Таким образом было показано, что динамика нижайшего по энергии конфайнментного экситона квантовых точек при низких температурах зависит от их окружения. Аналогичный вывод был сделан и при изучении тем же методом динамики электронных возбуждений
вквантовых точках в режиме сильного (CdSe) и промежуточного (CuBr) кон-
файнмента [110].
4. Оптика квантовых точек |
241 |
Высокочувствительная техника гетеродинного детектирования |
сигна- |
ла четырехволнового смешения света [111] была использована для изучения электронной динамики в самоорганизованных квантовых точках InGaAs/GaAs в режиме сильного конфайнмента [98]. Линейная зависимость T2−1 от температуры наблюдалась в области ниже 30 К. При 7 К T2 = 630 пс (~ 2 2 мкэВ). При экстраполяции температурной зависимости к 0 К значение T2 стремилось к удвоенному значению времени энергетической релаксации (T1), показывая, что в данной системе процесс дефазировки фундаментального перехода определяется неупругими столкновениями дырок с акустическими фононами. При этом из температурной зависимости T2 была определена энергия активации этих фононов (16 мэВ). Об измерениях времени распада когерентности фундаментального перехода в самоорганизованных квантовых точках InAlGaAs/GaAlAs методом четырехволнового смешения также сообщалось в работе [99]. Здесь среднее время дефазировки при 5 К составило 372 пс, что соответствует ~ 2 = 1:75 мкэВ. В то же время прямое измерение кинетики распада основного состояния этих квантовых точек дало значение его времени жизни 800 пс. Отсюда видно, что при ненулевых температурах (выше 5 К) вклад чистой дефазировки в распад когерентности существенно превышает вклад энергетической релаксации. Простая экстраполяция температурной зависимости к 0 К показывает, что в этом случае сбой когерентности в исследуемых точках может определяться релаксацией населенностей. Однако такой вывод надо принимать с осторожностью, поскольку, как и для квантовых точек на основе CuCl, заметные отклонения от линейной температурной зависимости могут иметь место при температурах ниже 2 К.
Важно отметить, что в некоторых из обсуждаемых выше систем квантовых точек (CuCl, CuBr и CdSe) возможно измерение T2 как методом выжигания провалов, так и с использованием техники фотонного эха. Сравнение данных, полученных этими методами, показало, что результаты могут сильно различаться [102]. Так же отмечено существенное различие времен дефазировки, полученных при временных´ нелинейно-оптических измерениях и при анализе однородной ширины линии фотолюминесценции одиночной квантовой точки. Природа различия в большинстве случаев остается непонятной. Поэтому важной задачей является развитие новых методов измерения времен дефазировки в неоднородно уширенных ансамблях квантовых точек, совместимых с уже существующими.
Мы предложили использовать для этих целей метод когерентного контроля вторичного свечения неоднородно уширенного ансамбля переходов [112]. Физические особенности этого метода применительно к изучению динамики квантовых точек изложены в следующем разделе.
Когерентный контроль спонтанного вторичного свечения
Поскольку процессы дефазировки в наноструктурах ослаблены по сравнению с объемными материалами, фемто- и пикосекундная экспериментальная
242 А.В. Федоров, А.В. Баранов
техника позволяет при их изучении использовать различные схемы квантового контроля, разработанные для атомных и молекулярных систем (см., например, [113]). Самой распространенной из них является схема когерентного контроля электронной подсистемы наноструктур, резонансно возбуждаемой парой коротких сфазированных импульсов света. Эффект заключается в том, что поляризации и населенности, наведенные первым импульсом, контролируются вторым и в зависимости от времени задержки полные поляризации и населенности могут увеличиваться или уменьшаться, т.е. представляют собой осцилляции на частотах, близких к несущей частоте импульсов !L. Благодаря конструктивной и деструктивной интерференции между поляризациями, индуцированными в исследуемой системе возбуждающими световыми импульсами, оптические отклики в зависимости от времени задержки имеют вид интерферограмм, подобных осцилляциям Рамсея [114]. Вследствие затухания индуцированной поляризации увеличение времени задержки приводит к уменьшению амплитуды осцилляций и, следовательно, к падению эффективности когерентного контроля. В то же время, поскольку форма интерферограмм определяется скоростью потери когерентности, техника двухимпульсного возбуждения может быть использована для изучения динамики спектроскопических переходов. При этом регистрироваться могут сигналы индуцированного отражения [115] (метод накачка–зондирование), четырехволнового смешения [116] или спонтанного вторичного свечения как в режиме реального времени [117, 118], так и интегрированные по времени [119]. Важной особенностью схемы когерентного контроля является то, что высокочастотные осцилляции измеряемых сигналов промодулированы медленной огибающей, форма которой содержит информацию о скорости дефазировки резонансного оптического перехода.
Другой интересной особенностью когерентных процессов, развивающихся при оптическом возбуждении квантовой системы парой сфазированных импульсов, является возможность контроля электронных волновых функций системы в диапазоне времен, сравнимых с временами дефазировки квантовых состояний. Использование техники когерентного контроля позволяет получить информацию об амплитудах и относительных фазах волновых функций, а также манипулировать ими, меняя время задержки и взаимную поляризацию пары импульсов. Таким образом, возникает возможность переводить систему в заданное квантовое состояние и детектировать наличие системы в том или ином состоянии. Техника когерентного контроля успешно использовалась и в полупроводниковых материалах, включая квантовые ямы, для которых была продемонстрирована возможность контроля фототока [120], населенности и ориентации экситонов [115], а также люминесценции [119]. Оказалось, что времена фазовой релаксации электронных состояний в таких системах не превышают десятка пикосекунд, задавая, тем самым, предельное время хранения квантовой информации. Ожидается, что использование квантовых точек позволит существенно увеличить это время: из общих фундаментальных законов сохранения энергии и импульса следует, что для идеальных
4. Оптика квантовых точек |
243 |
квантовых точек времена фазовой релаксации при низких температурах могут быть ограничены радиационным временем жизни, т.е. составлять несколько наносекунд [121]. Таким образом, существуют многообещающие перспективы применения когерентного контроля квантовых точек в различных схемах квантовых вычислений и даже когерентной обработки информации на уровне индивидуальных квантовых систем [122], поскольку возможен когерентный контроль одиночной квантовой точки [123].
С точки зрения определения релаксационных параметров наноструктур, особый интерес представляют интегрированные по времени сигналы резонансного спонтанного вторичного свечения, поскольку измерения в режиме реального времени существенно сложнее. Кроме того, для устойчивой регистрации спонтанного вторичного свечения можно использовать импульсные световые поля, достаточно слабые по сравнению с теми, которые применяются в методе накачка–зондирование и экспериментах по четырехволновому смешению. Это позволяет исключить влияние возбуждающего излучения на величину констант энергетической и фазовой релаксации. Схема когерентного контроля с регистрацией интегрированного по времени квазиупругого вторичного свечения была успешно использована для определения скорости дефазировки оптических переходов в экситонные состояния квантовых ям [119]. При изучении квантовых точек возникает дополнительная трудность, связанная с большим неоднородным уширением их оптических спектров. Ее можно обойти с помощью новой и чрезвычайно сложной техники зондирования одиночной квантовой точки, которая будет рассмотрена в следующем разделе.
Привлекательность метода когерентного контроля заключается в том, что при определенных условиях интегрированный по времени сигнал I( ) оптического отклика на двухимпульсное возбуждение в зависимости от времени взаимной задержки между импульсами может быть представлен в виде интерферограммы
I( ) 1 + K( ) cos(!i ); |
(4.94) |
осциллирующей на высокой частоте !i и промодулированной медленно меняющейся огибающей функцией K( ), которая содержит информацию о скоростях дефазировки резонансных оптических переходов.
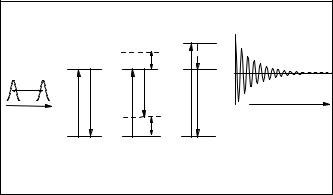
Для выяснения потенциальных возможностей когерентного контроля с точки зрения исследования динамики элементарных возбуждений квантовых точек, обладающих большим неоднородным уширением оптических переходов, были рассмотрены три компоненты спонтанного вторичного свечения: квазиупругое вторичное свечение [124], вторичное свечение с участием оптического фонона [125] и термализованная люминесценция [126]. Соответствующие им оптические переходы представлены на рис. 4.25. Анализ проинтегрированных по времени сигналов спонтанного вторичного свечения показал, что в общем случае они не могут быть представлены в виде одиночной интерферограммы, подобной (4.94). На самом деле, сигналы представляют собой суперпозицию интерферограмм, осциллирующих на различных часто-
244 А.В. Федоров, А.В. Баранов |
|
|
||
|
|
2 |
K(τ ) cos(ωiτ ) |
|
1 |
1 |
Ω 1 |
τ |
|
τ |
ω |
ω20 |
||
|
||||
|
10 |
ω |
|
|
ω10 |
ω D |
D |
ωD ω10 |
|
Ω |
||||
0 |
0 |
0 |
|
|
|
(a) |
(б) |
(в) |
|
Рис. 4.25. Диаграммы энергетических уровней квантовой точки и оптических переходов при возбуждении парой сфазированных лазерных импульсов с переменной взаимной задержкой . В результате возникает: квазиупругое вторичное свечение (a), вторичное свечение с участием оптического фонона (б) и термализованная люминесценция (в). Зависимость сигналов от показана схематически на вставке.
тах и промодулированных различными огибающими функциями. Кроме того, сигналы сильно зависят от формы возбуждающих импульсов и спектральных свойств регистрирующей системы. Для того чтобы проинтегрированные по времени компоненты вторичного свечения могли быть описаны выражением (4.94), необходимо выполнение ряда условий. Прежде всего, спектральная ширина лазерных импульсов должна быть много больше, чем скорости дефазировки оптических переходов . В этом случае рассматриваемая система большую´ часть времени эволюционирует в отсутствие каких-либо внешних возмущений, т. е. затухание свободной поляризации, населенностей и сигналов вторичного свечения контролируется только релаксационными константами . С другой стороны, величина должна быть достаточно мала, чтобы несколько уровней системы не могли возбуждаться одновременно. Таким образом, необходимо выполнение следующего двойного неравенства<< << ", где " равна частоте оптического фонона или частотному зазору между резонансным и ближайшим к нему экситонным уровнем. Кроме того, рассмотрение неоднородно уширенных ансамблей квантовых точек было ограничено системами, для которых неоднородные ширины экситонных переходов значительно превышают .
Если перечисленные выше условия выполняются, то сигнал квазиупругого вторичного свечения (рис. 4.25a) может быть описан выражением (4.94), когда при изучении неоднородно уширенного ансамбля квантовых точек используется фильтр с узкой полосой пропускания D. Соответствующие параметры интерферограмм представлены в табл. 4.1. Если скорость чистой дефазировки pd много меньше, чем обратное время жизни экситона 1, то

4. Оптика квантовых точек |
245 |
Таблица 4.1. Параметры интерферограммы (K( ) и !i) для квазиупругого вторичного свечения: !D – частота детектирования; 2 = 1=2+ pd – полная скорость дефазировки резонансного оптического перехода; 0, 1, и pd – обратные времена жизни фотона, экситона и скорость чистой дефазировки, соответственно.
D <<
exp[−( D + 0=2) ], !D для pd << 1 exp[−( D + 2 2) ], !D для pd >> 1
будет наблюдаться квазиупругое рассеяние. В противоположном случае сигнал осциллирующий на частоте детектирования !D может быть отнесен к резонансной люминесценции. Важно отметить, что в неоднородно уширенных ансамблях проявляется эффект “насыщения” огибающей. Он состоит в том, что при уменьшении полосы пропускания фильтра огибающая стремится к функции exp(− 0=2) или exp(−2 2 ), где 0 – обратное время жизни фотона. Второе проявление неоднородного уширения заключается в том, что затухание люминесценции контролируется удвоенной величиной 2.
Естественным ограничением когерентного контроля спонтанного вторичного свечения при исследовании релаксационных параметров является требование достаточно большого резонансного усиления сигнала. В противном случае полезный сигнал будет замаскирован паразитным светом или сигналом поверхностного рассеяния. В этом смысле, большой интерес представляет когерентный контроль спонтанного вторичного свечения на частоте, отличной от несущей частоты импульсов, например на стоксовой частоте вторичного свечения с участием оптического фонона или на частоте термализованной люминесценции.
Для вторичного свечения с участием оптического фонона (рис. 4.25б) наиболее важные случаи, когда проинтегрированный по времени сигнал может быть представлен одиночной интерферограммой, собраны в табл. 4.2. В случае неоднородно уширенного ансамбля, когда используется узкопо-
Таблица 4.2. Параметры интерферограммы (K( ) и !i) для вторичного свечения с участием оптического фонона при входном резонансе: ph и – обратное время жизни и частота оптического фонона.
D <<
exp[−( D + ph=2) ], !D + для pd << 1 exp[−( D + 2 2 + ph=2) ], !D + для pd >> 1
лосный фильтр, сигнал может быть приписан резонансному комбинационному рассеянию, если pd << 1 и резонансной люминесценции, еслиpd >> 1. Неоднородное уширение приводит к эффекту насыщения оги-

246 А.В. Федоров, А.В. Баранов
бающей, которая стремиться при уменьшении D к функции exp(− ph=2) или exp[−( 2 + ph=2) ], где ph – обратное время жизни фонона. Сигнал резонансной люминесценции осциллирует на частоте !D + и его затухание контролируется параметром 2 2 + ph=2 . Таким образом, для определения 2 необходимо из независимых экспериментов найти ph и наоборот.
Для изучения скоростей релаксации высокоэнергетических экситонных переходов можно осуществить когерентный контроль термализованной люминесценции (рис. 4.25в). Соответствующие параметры интерферограмм представлены в табл. 4.3. Анализ показал, что когерентный контроль терма-
Таблица 4.3. Параметры интерферограммы (K( ) и !i) для термализованной люминесценции: 20 и 10 – скорости полной дефазировки переходов с частотами !20 и !10 в возбужденное и основное экситонное состояние, – отношение между конфайнментными энергиями возбужденного и основного экситонных состояний.
D <<
exp[−( 20 + ( 10 + D)) ], !20 − (!10 − !D)
лизованной люминесценции может быть использован при изучении неоднородно уширенных ансамблей квантовых точек, если неоднородное уширение может быть описано статистической моделью линейной регрессии, в которой частоты экситонных переходов являются случайными и взаимозависимыми величинами с сильной корреляцией. Тогда, сигнал термализованной люминесценции для узкополосного фильтра, как и в случаях рассмотренных выше, проявляет эффект насыщения огибающей. В результате эта функция стремится к предельной величине exp[−( 20 + 10) ] для D << 20 + 10, где 10 – скорость дефазировки перехода с частотой !10 в основное экситонное состояние. Кроме того, осцилляции сигнала происходят на частоте !20 − (!10 −!D),
вто время как их затухание определяется линейной комбинацией 20 + 10, где > 1 – отношение между конфайнментными энергиями возбужденного и основного экситонных состояний. Следует подчеркнуть, что эффект насыщения термализованной люминесценции прямо показывает, что упомянутая выше статистическая модель может описывать неоднородное уширение оптических спектров.
Теория когерентного контроля спонтанного вторичного свечения полупроводниковых квантовых точек показывает, что этот спектроскопический метод может применяться для исследования динамики элементарных возбуждений
вансамбле точек с большим неоднородным уширением. Установлены релаксационные параметры, которые могут быть надежно определены данным методом и найдены оптимальные условия проведения экспериментов. Полученные результаты были успешно использованы при изучении индуцированных механическим напряжением квантовых точек на основе InGaAs/GaAs [112]. Применение теоретической модели когерентного контроля вторичного свече-
