96 Н.Н. Розанов
распространяться в совершенном фотонном кристалле (вдали от дефекта), в нем потери излучения на изгибах резко уменьшаются. Как показывают расчеты [90] и эксперимент [91], в фотонно-кристаллических волноводах с радиусом изгиба, превышающим длину волны излучения, высокое пропускание достижимо почти для всех частот, отвечающих фотонной запрещенной зоне.
2.5.1. Неидеальные фотонные кристаллы
Выше были продемонстрированы последствия таких отклонений от идеальной схемы бесконечного фотонного кристалла, как учет его пространственной ограниченности, последовательное расположение нескольких ограниченных фотонных кристаллов (связанные микрорезонаторы) и введение отдельных дефектов в фотонные кристаллы. Интересно обобщение рассматриваемых структур на случай не периодического, а квазипериодического изменения характеристик среды. Это аналогично замене кристаллов на квазикристаллы, обладающие только дальним порядком [92]. Численное моделирование показывает возможность фотонных квазикристалов с запрещенной зоной [93, 94]. Примыкают к таким структурам изображенные на рис. 2.27 двумерные решетки Пенроуза, получаемые укладкой на плоскости ромбов двух типов с одинаковой длиной сторон. Хотя эта структура непериодическая, она обладает дальним порядком и вращательной симметрией 10-го порядка. Соответственно картина дифракции на такой решетке в дальней зоне обладает выраженными пиками. Эта картина (рис. 2.28) получена при освещении излучением гелий-неонового лазера образца кварца, в котором были вытравлены цилиндры с диаметром 3 мкм. Цилиндры расположены, как это указано на рис. 2.27, причем длины сторон ромбов составляют 10 мкм. Экспериментальные результаты хорошо согласуются с расчетом, в котором учитывается сравнительно небольшое (5) число векторов эффективной обратной решетки [95, 96].
В реальном фотонном кристалле строгая периодичность распределения показателя преломления нарушается, что ставит вопрос о сохранении запрещенной зоны в них. Для ответа на этот вопрос привлекается численное моделирование [97]. Более проста одномерная геометрия, для которой показатели преломления чередующихся слоев A и B определяются соотношением
nA;B = n0(1 + P) ± g:
Здесь величина P принимает случайные значения в диапазоне от −1=2 до 1/2. Тем самым глубина относительных флуктуаций задается параметром .
В случайной структуре сохраняются моды излучения, но они обладают конечным временем жизни, что отвечает комплексности собственных частот. На рис. 2.29 представлены результаты расчета характеристик мод — вещественные части частот ! и времена жизни — для 1000 структур с различной степенью разупорядоченности . Видно, что при < 0.1 флуктуации сужают запрещенную зону, но сохраняют ее существование, тогда как при > 0.15
2. Оптическое излучение... |
97 |
частоты мод случайных микрорезонаторов заполняют уже всю зону. Зависимость от столь резка, что практически можно говорить о пороге, причем согласно расчетам пороговое значение th ≈ √(!=!0)=3. Сходные результаты справедливы и для двумерных разупорядоченных фотонных кристаллов [97]. В фотонном кристалле с хаотически распределенными вакансиями спектры пропускания содержат сравнительно узкие полосы, причем максимальное пропускание заметно ниже, чем при регулярном расположении вакансий (рис. 2.30).
Рис. 2.27. Двумерная решетка Пенроуза. Черные кружки отвечают полым цилиндрам. Широкие стрелки внизу указывают направление волнового вектора падающего света, черные стрелки и числа в скобках отвечают различным направлениям распространения света. Кривые слева и сверху представляют профили показателя преломления, усредненные по сечениям, ортогональным направлениям (00110) и (10000) [95].
Рис. 2.28. Дифракция света на двумерной решетке Пенроуза [95, 96].
98 Н.Н. Розанов
2.5.2. Нелинейные двумерные фотонные кристаллы
Как указывалось выше, оптическая нелинейность может сделать возможным распространение излучения с частотой, даже отвечающей фотонной запре-
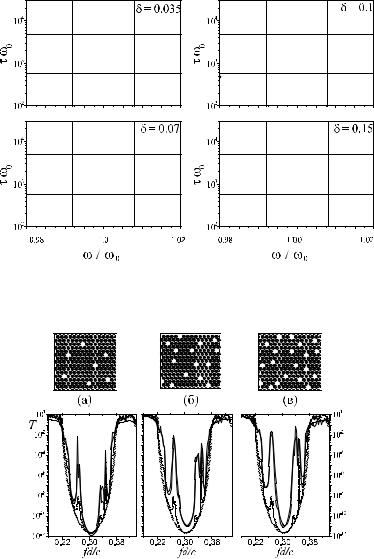
Рис. 2.29. Частоты собственных мод ! и их времена жизни для 1000 одномерных разупорядоченных структур с параметром относительных флуктуаций = 0.035, 0.07, 0.1 и 0.15 [97].
Рис. 2.30. Двумерные фотонные кристаллы с хаотически распределенными вакансиями (сверху) и их спектры при концентрации вакансий 3 (а), 6.7 (б) и 8.3 % (в) (внизу, сплошные линии). Штриховые линии показывают спектры пропускания идеального фотонного кристалла, а пунктир — спектры структуры с одиночной вакансией [98].
2. Оптическое излучение... |
99 |
щенной зоне. Это обстоятельство существенно для формирования двумерных солитонов в фотонных кристаллах с нелинейным показателем преломления.
В качестве примера удобно рассмотреть изображенный на рис. 2.24б фотонный кристалл, составленный из цилиндров (стержней) двух типов [99]. Цилиндры первого типа — линейные с радиусом r0, а второго типа — нелинейные (керровская нелинейность), с радиусом rd. Нелинейные стержни можно трактовать как дефекты, погруженные в идеальную решетку линейных стержней. Используется обобщение системы дискретных НУШ (2.29) для амплитуд En;m(z) = E(rn;m; z) поля в месте расположения дефекта с индексами n; m:
|
@En;m |
∑ |
|
i |
|
− En;m + Jn−k;m−l("d0 + |Ek;l|2)Ek;l: |
(2.39) |
@z |
|||
|
|
k;l |
|
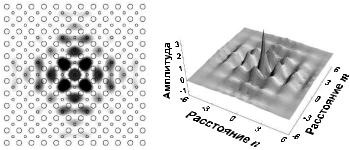
Коэффициенты связи Jn−k;m−l определяются функцией Грина идеальной решетки линейных стержней. Практически для получения достаточной точности требуется учитывать при суммировании не менее 10 соседних стержней. Введение в (2.39) дополнительного члена с временной производной позволяет рассматривать случай импульсов излучения, а также проверять устойчивость нелинейных структур поля. Результаты расчета двумерного солитона с частотой, лежащей в запрещенной зоне нелинейного фотонного кристалла, представлены на рис. 2.31. Как и следовало ожидать для консервативных систем, такие солитоны образуют семейство со сплошным спектром, например, максимальной интенсивности.
Нелинейные квазипериодические структуры исследованы еще недостаточно полно. Отметим здесь только существование квазипериодических параметрических солитонов в подобных системах с квадратичной оптической нелинейностью [100].
Еще одной важной областью применения нелинейных фотонных кристаллов служат микроструктурированные оптические волокна. В них реализуется усиление нелинейно-оптических взаимодействий, что приводит ко многим практическим приложениям в области предельно коротких лазерных импуль-
Рис. 2.31. Контуры интенсивности (слева) и объемный вид (справа) солитона с частотой, отвечающей запрещенной зоне двумерного фотонного кристалла [99].