90 Н.Н. Розанов
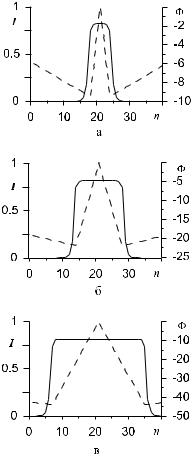
значений контрольного параметра [39]. В рассматриваемом случае такой эффект также имеет место. Это видно из приведенных на рис. 2.20 структур, полученных при различных значениях ширины начального распределения. Особенностью дискретных солитонов является резкое (близкое к ) изменение фаз в соседних волноводах, что не имеет аналога в континуальном пределе. Меняя значение коэффициента усиления, можно получить волны переключения, фронт которых движется в ту или иную сторону (рис. 2.21). Естественно, что для периодических структур невозможен реализующийся для однородных систем вариант структур с эволюцией, отвечающей простому переносу, типа E = E(x − vz). Движение всегда сопровождается модуляцией с периодом, отвечающим периоду системы. Отметим также видные на рис. 2.21 осцилляции интенсивности вблизи фронта движущейся волны переключения.
Перейдем теперь к локализованным (солитоноподобным) диссипативным структурам. На рис. 2.22 представлены два типа установившихся поперечно неподвижных солитонов с малым изменением фазы у соседних волноводов. Для первого типа (а) максимум интенсивности достигается на одном волноводе, а для второго типа (б) — на двух соседних волноводах. Этот вариант примыкает к континуальному пределу, хотя ширина распределения поля не столь велика. Наконец, на рис. 2.23 изображено установившееся поперечное движение дискретного диссипативного солитона. Фаза от волновода к волноводу меняется сравнительно слабо, хотя солитон обладает небольшой шириной. Здесь также видны периодические изменения формы движущегося солитона.
Таким образом, в рассматриваемой системе реализуются локализованные структуры поля как родственные известным в однородных системах, так и не имеющие аналогов, с почти противофазным распределением полей в соседних волноводах. Напомним, что дискретные диссипативные солитоны, как и другие диссипативные солитоны, обладают повышенной устойчивостью к шумам, что и определяет их потенциал для информационных приложений. Кроме того, как и в случае брэгговских солитонов, поперечное движение консервативных дискретных солитонов приводит к потерям их энергии и торможению такого движения, тогда как для аналогичных диссипативных солитонов потери энергии компенсируются усилением и возможным становится поперечное движение с периодически меняющейся формой солитонов. Это обстоятельство важно для реализации поперечных сдвигов массивов солитонов, которыми кодируется распределенная в сечении системы волноводов информация.
2.5. Двумерные фотонные кристаллы
Наиболее распространенные типы современных двумерных фотонных кристаллов можно моделировать решетками цилиндров, оптические свойства которых отличаются от свойств окружающей среды, а оси параллельны друг
2. Оптическое излучение... |
91 |
Рис. 2.20. Установившиеся профили интенсивности (сплошные линии) и фазы (штриховые линии) для трех пар неподвижных волн переключения, формирующихся при начальном возбуждении различной ширины (ширина возрастает от а к в).
другу. Практически их можно получить, формируя лазерным излучением либо разрежения в однородной среде, которые далее могут быть заполнены другой средой, либо, напротив, сгущения в фотополимеризующейся среде. Примеры таких идеальных двумерных фотонных кристаллов представлены на рис. 2.24 для цилиндров одного (а) и двух (б) типов. На рис. 2.25 изображены также трехмерные фотонные кристаллы типа “поленицы”, которые изготавливаются послойно с периодическим изменением направления осей цилиндров. В линейном режиме высокая дисперсия фотонных кристаллов приводит к возможности построения “суперпризм” с аномально высокой чувствительностью угла отклонения к длине волны излучения. В фотонном кристалле, как и в дифракционной решетке, можно управлять распределением излуче-
92 Н.Н. Розанов
z = 0 |
z = 0 |
z = 100 |
z = 40 |
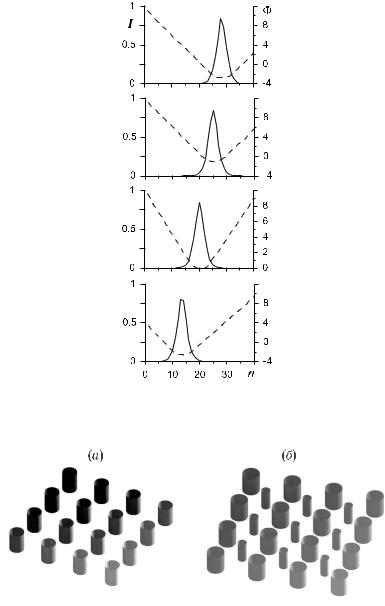
Рис. 2.21. Мгновенные профили интенсивности (сплошные линии) и фазы (штриховые линии) фронта движущихся направо (а, g0 =2.09) и налево (б, g0 =2.113) волн переключения.
Рис. 2.22. Установившиеся профили интенсивности (сплошные линии) и фазы (штриховые линии) для двух типов неподвижных диссипативных дискретных солитонов.
ния по порядкам дифракции. Это позволяет реализовать, например, аналог среды с “отрицательным показателем преломления”, что полезно для ряда приложений. Весьма перспективны для приложений и нелинейные фотонные кристаллы.
Для получения достаточно широких запрещенных зон показатель преломления цилиндров выбирается существенно отличающимся от показателя преломления среды. Это обстоятельство исключает возможность применения теории возмущений по глубине модуляции показателя преломления уже в линейном режиме. В частном случае распространения излучения вдоль оси
2. Оптическое излучение... |
93 |
Рис. 2.23. Мгновенные профили интенсивности (сплошные линии) и фазы (штриховые линии) движущегося диссипативного дискретного солитона; продольная координата изменяется от профиля к профилю на z = 6.
Рис. 2.24. Двумерные фотонные кристаллы, формируемые цилиндрами одного (а) или двух (б) типов.
двумерной системы параллельных цилиндров — одномодовых волноводов со слабой связью — допустим переход к дискретному описанию, представленному в предыдущем разделе. При этом естественным образом учитывается
94 Н.Н. Розанов
Рис. 2.25. Фрагмент трехмерного фотонного кристалла типа “поленицы”.
и нелинейность оптических сред, что позволяет описать двумерные дискретные солитоны. В общей ситуации дисперсионные разложения и структура зон двумерного линейного фотонного кристалла находятся численно с использованием теории Флоке–Блоха и разложением поля в спектр плоских волн. Более прост случай распространения монохроматического излучения с частотой ! ортогонально осям цилиндров, когда электрическая напряженность направлена вдоль их осей, E(r; t) = Re[ezA(r) exp (−i!t)]. Тогда решению подлежит скалярное уравнение Гельмгольца
!2 |
|
2A(r) + c2 "(r)A = 0: |
(2.36) |
Если этот этап выполнен, то далее слабость нелинейно-оптических эффектов позволяет использовать для исследования солитонов тот или иной вариант теории возмущений по интенсивности излучения.
Важным свойством фотонных кристаллов служит возможность целенаправленного введения в них дефектов. Примером служит введение “дефектного стержня” с радиусом rd и диэлектрической проницаемостью "d в двумерный фотонный кристалл с расстоянием между стержнями a. Это позволяют реализовать принципиально новый тип линейных фотонно-кристаллических волноводов на основе фотонной запрещенной зоны. Напомним, что в обычном волноводе используется явление полного внутреннего отражения, для чего показатель преломления сердцевины выбирается превышающим показатель преломления оболочки. В случае же фотонного кристалла и частоты излучения, лежащей в его запрещенной зоне, излучение будет локализованным около дефектного стержня, так как оно не может распространяться в совершенном кристалле без дефекта (с диэлектрической проницаемостью "0(r)). Пространственное распределение диэлектрической проницаемости представляется в виде
"(r) = "0(r) + "d(r);
где при выборе продольной оси координат вдоль оси дефектного стержня z
"d(r) = |
{ "d − "0(r); |
r < rd: |
|
0; |
r > rd; |
2. Оптическое излучение... |
95 |
Рис. 2.26. Локализованная мода, поддерживаемая единственным дефектным стержнем с радиусом rd = 0:1a в двумерной решетке стержней с r0 = 0:18a и "0 = 11:56. Положение стержней указано кружками [89].
Теперь уравнение Гельмгольца (2.36) примет вид
[ 2 |
+ ( |
! |
) |
2 |
"0(r)] |
!2 |
|
|
|
|
|
A(r) = − |
|
"d(r)A: |
(2.37) |
||||
c |
|
c2 |
|||||||
Определяем функцию Грина G(r; r′; !) стандартным соотношением
[ 2 + ( |
c ) |
"0(r)] |
G(r; r′; !) = − (r − r′): |
(2.38) |
|
|
! |
|
2 |
|
|
Практически эту функцию нужно находить численно. Тогда уравнение (2.37) записывается в виде
A(r) = !2 Z∞ G(r; r′; !) "d(r′)A(r′) d2r′: c2
−∞
Численное решение этого интегрального уравнения позволяет найти профиль мод дефекта A(r). Пример такого решения приведен на рис. 2.26 для случая единственного дефектного стержня с тем же показателем преломления, что и у основных стержней, но с меньшим радиусом. Представленные контуры амплитуды поля подтверждают, что свет с частотой, лежащей внутри запрещенной зоны, локализован в области дефекта.
Такая локализация света дефектом предоставляет возможность формирования волноводов с уникальными свойствами. Это особенно актуально в связи с необходимостью резких изгибов световодов для создания компактных “интегральных оптических схем”. В обычном световоде, основанном на эффекте полного внутреннего отражения, на изгибе теряется значительная часть мощности излучения, которая вытекает из сердцевины и свободно распространяется в оболочке. Так как в волноводе на основе брэгговского отражения излучение с частотой, лежащей внутри запрещенной зоны, не может