
- •1. Фотонные кристаллы
- •1.1. Концепция
- •1.1.1. Электроны в кристаллических структурах
- •1.1.2. Электромагнитные волны в кристаллических структурах
- •1.1.3. Фотонное твердое тело: распространение и локализация электромагнитных волн в условиях сильного многократного рассеяния
- •1.2. Синтез и свойства фотонных кристаллов
- •1.2.1. Фотонные кристаллы в природе
- •1.2.2. Одномерные периодические структуры
- •1.2.3. Двумерные периодические структуры
- •1.2.4. Трехмерные периодические структуры
- •1.3. Испускание и рассеяние излучения в фотонных кристаллах: роль плотности фотонных состояний
- •1.3.1. Интегральная и локальная плотности состояний
- •1.3.2. Спонтанное испускание фотонов
- •1.3.3. Тепловое излучение
- •1.3.4. Комбинационное рассеяние
- •1.3.5. Резонансное (релеевское) рассеяние
- •1.4. Заключение
- •Список литературы
- •2. Оптическое излучение в линейных и нелинейных периодических структурах
- •2.1. Введение
- •2.2.1. Квазиоптическое приближение
- •2.2.2. Линзовые волноводы и лазерные резонаторы
- •2.2.4. Мелкомасштабная самофокусировка в периодических системах
- •2.2.5. Квазисинхронное параметрическое взаимодействие
- •2.3. Одномодовый световод с брэгговской решеткой
- •2.3.1. Двунаправленное распространение излучения
- •2.3.2. Брэгговские солитоны
- •2.3.3. Оптическая бистабильность и переключение
- •2.3.4. Полупроводниковые микрорезонаторы
- •2.4. Связанные световоды
- •2.5. Двумерные фотонные кристаллы
- •2.5.1. Неидеальные фотонные кристаллы
- •2.5.2. Нелинейные двумерные фотонные кристаллы
- •2.6. Заключение
- •Список литературы
- •3. Оптика квантовых ям и сверхрешеток
- •3.1. Классификация гетероструктур
- •3.2. Размерное квантование электронных состояний
- •3.3. Правила отбора при оптических переходах
- •3.3.1. Междузонные и внутризонные оптические переходы между подзонами размерного квантования
- •3.3.2. Поляризационные свойства оптических переходов из подзон тяжелых и легких дырок
- •3.4. Резонансное отражение и поглощение света в структурах с квантовыми ямами
- •3.5. Вторичное свечение гетероструктур
- •3.6. Квантовые микрорезонаторы
- •3.7. Заключение
- •Список литературы
- •4. Оптика квантовых точек
- •4.1. Введение
- •4.1.1. Состояния размерного квантования электронных и фононных возбуждений квантовых точек
- •4.1.2. Электрон-фононное взаимодействие в квантовых точках
- •4.1.3. Динамика электронных возбуждений квантовой точки
- •4.2. Оптические методы исследования квантовых точек
- •4.2.1. Изучение энергетической структуры электронных возбуждений
- •4.2.3. Исследование динамики элементарных возбуждений квантовых точек
- •4.2.4. Оптическая спектроскопия одной квантовой точки
- •4.3. Применение квантовых точек
- •4.3.1. Лазеры на квантовых точках для волоконной связи
- •4.3.2. Квантовые точки в биологии и медицине
- •Список литературы
- •5. Оптические резонансные свойства металлических наночастиц
- •5.1. Введение
- •5.2. Резонансы Ми отдельных металлических наночастиц
- •5.2.1. Эффект размера
- •5.2.2. Эффекты формы
- •5.3. Действие окружения на резонансы металлических наночастиц
- •5.3.1. Электродинамические эффекты
- •5.3.2. Контактные эффекты
- •5.4. Нелинейные оптические свойства металлических наночастиц
- •5.4.1. Генерация высших гармоник
- •5.4.2. Оптические комбинационные процессы
- •5.5. Неоднородные системы металлических наночастиц
- •5.5.1. Структурные параметры неоднородных систем
- •5.5.2. Измерение релаксационных параметров индивидуальных резонансов в неоднородных системах
- •5.6. Применения металлических наночастиц, связанные с их оптическими свойствами
- •5.7. Заключение
- •Список литературы
2. Оптическое излучение... |
79 |
2.3.4. Полупроводниковые микрорезонаторы
Представленная теория описывает не только световоды, но и широкий круг структур с брэгговским резонансным отражением. Как показано в [72], брэгговский резонанс в полупроводниковых структурах множественных квантовых ям может быть использован для быстрого (субпикосекундного) переключения. Важным примером более сложной геометрии служат полупроводниковые микрорезонаторы, эквивалентные интерферометрам Фабри–Перо, в которых зеркала заменены брэгговскими структурами. На рис. 2.9 показано продольное ступенчатое распределение показателя преломления, формирующее два связанных линейных микрорезонатора, а также соответствующие распределения напряженностей электрического и магнитного полей. Спектр пропускания этой системы, приведенный на рис. 2.10, демонстрирует обострение резонансов при увеличении числа пар слоев внешних зеркал, сопровождающимся увеличением их эффективного коэффициента отражения, а также сближение резонансов при увеличении числа пар слоев среднего зеркала.
2.4. Связанные световоды
Важный специальный случай периодического изменения показателя преломления отвечает системе слабо связанных одномодовых волноводов типа изображенной на рис. 2.11. Условие одномодовости, как пояснялось в разделе 2.2
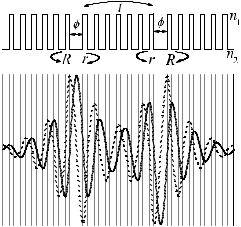
Рис. 2.9. Профиль показателя преломления для двух связанных микрорезонаторов, характеризующихся фазовым набегом , коэффициентами отражения зеркал R и r и связанных средним зеркалом с коэффициентом пропускания t (сверху). Профили напряженностей электрического (сплошная линия) и магнитного (штриховая линия) полей (снизу). Показатели преломления принимают значения n1 =1.45 (SiO2) и n2 =2.3 (TiO2) [73].
80 Н.Н. Розанов
для одиночного световода, существенно упрощает анализ структуры поля, сводя геометрию схемы фактически к одномерной. Учет же слабой связи одномодовых световодов в приближении связанных мод приводит к замене единственного уравнения (2.7) на систему связанных уравнений для комплексных амплитуд мод различных световодов, вид которой зависит от типа нелинейности и режима излучения (непрерывный или импульсный). В данном случае имеет место одномерное поперечное периодическое изменение свойств схемы. В наиболее простом случае линейной системы одинаковых световодов, непрерывного (монохроматического) излучения и керровской нелинейности эти уравнения имеют вид [75]
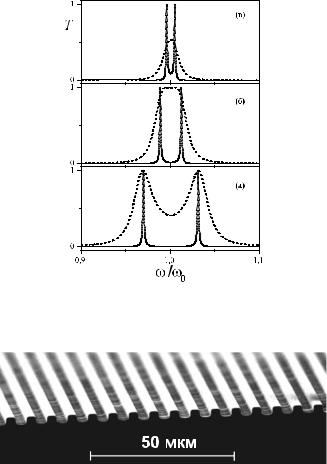
Рис. 2.10. Спектры пропускания двух связанных микрорезонаторов. Внешние зеркала состоят из 6 (сплошные линии) или 3 (штриховые линии) пар слоев. Число пар слоев внутреннего зеркала: 2 (а), 4 (б) и 5 (в) [73].
Рис. 2.11. Система слабо связанных оптических волноводов на основе полимеров (перед нанесением полимерного покрытия), состоящая из 75 одномодовых волноводов [74].

|
|
2. Оптическое излучение... |
81 |
i |
dAn |
+ An + C(An−1 + An+1) + |An|2An = 0: |
(2.29) |
dz |
Здесь An — амплитуда моды n-го волновода, параметры и имеют прежний смысл постоянной распространения и эффективного коэффициента нелинейности, а новым параметром является коэффициент линейной связи волноводов C, причем считается, что такая связь реализуется только для соседних световодов. В идеальной периодической системе световодов c расстоянием между световодами их число бесконечно. Если система конечна, то вид граничных условий тем не менее может быть несущественным, например для светлых солитонов, у которых поле эффективно отлично от нуля только в ограниченном числе световодов.
Систему (2.29) называют дискретным нелинейным уравнением Шредингера. Она переходит в обычное нелинейное уравнение Шредингера (НУШ) в так называемом континуальном пределе. В этом пределе (2.29) трактуется как конечно-разностная аппроксимация континуального НУШ с заменой дифракционного члена
@2A → An−1 − 2An + An+1 ; @x2 h2
где An = A(x = nh) и h — шаг дискретизации. Противоположный (антиконтинуальный) предел C = 0 отвечает несвязанным световодам. Дискретное НУШ (2.29) обладает двумя интегралами движения, отвечающими сохранению пол-
ной мощности P и величины H, где |
|2 − 2 |An|4) |
|
|||||
P = |
n |
|An|2; |
H = |
n |
( |An|2 + C|An − An−1 |
: |
|
|
∑ |
|
|
∑ |
|
1 |
|
В импульсном режиме существен учет дисперсии, для чего (2.29) следует дополнить членами с временными´ производными. Уже для трех связанных нелинейных световодов система (2.29) не решается аналитически и может обладать даже хаотической динамикой [76, 77]. Прежде чем перейти к представлению результатов численных расчетов, обсудим качественные отличия, вносимые периодичностью и дискретностью рассматриваемой системы, по сравнению со случаем однородной среды.
Напомним, что интересующая нас система служит частным случаем периодических систем. Поэтому в линейном режиме (слабое излучение, предел→ 0) к ней также применима общая теория Флоке–Блоха. В линейном случае (2.29) имеет простое решение с дискретными функциями Блоха в виде плоских волн с волновым вектором, наклоненным по отношению к основной оси распространения z (ввиду использования квазиоптического приближения угол наклона должен быть малым):
An(z) = A exp (inkxd + ikzz): |
(2.30) |
После подстановки (2.30) в (2.29) получается следующее дисперсионное соотношение между продольной и поперечной компонентами волнового вектора [78]:
82 Н.Н. Розанов
kz = + 2C cos (kx ): |
(2.31) |
Сравним (2.31) с соответствующим дисперсионным соотношением для случая однородной среды с постоянной диэлектрической проницаемостью "0
|
|
|
k2x |
|
|
! |
|
|
|
|
|
kz = √k02 − k2x ≈ k0 − |
|
|
|
|
|
|
|||||
; |
k0 = |
√"0: |
(2.32) |
||||||||
2k0 |
c |
||||||||||
Приближенное извлечение квадратного корня в (2.32) отвечает квазиоптическому приближению. Основное отличие (2.31) от (2.32) связано с периодичностью зависимости kz(kx) в первом случае, тогда как во втором случае эта зависимость монотонна. Это отвечает возникновению для периодической системы световодов зоны Бриллюэна, отвечающей неравенству
|kx | < :
Дифракционный параметр, описывающий дифракцию в квазиоптическом приближении и определяемый как D0 = @2kz=@k2x, для однородной среды постоянен и отрицателен, D0 = −1=k0. Для периодической системы световодов D0 = −2C 2 cos (kx ), т.е. этот параметр периодически зависит от kx и меняет знак. В квазиоптическом приближении дифракция вообще исчезает при kx = ( =2 )(2n + 1) и становится аномальной в интервалах − =2 + n < kx <=2 + n , n = 0; ±1; ±2; : : : . Этот эффект, означающий возможность управления характером дифракции в периодических средах, называется дискретной дифракцией.
Для линейной задачи решениями (2.29) будут служить и линейные комбинации дискретных блоховских функций, причем их следует выбирать так, чтобы на входе реализовался задаваемый профиль пучка излучения. Если, например, на входе возбуждается только один световод, то на конечном расстоянии z распределение интенсивностей мод In = |An|2 определяется функцией Бесселя: In = I0 Jn2(2Cz) [18]. Видно, что, несмотря на поперечную периодичность показателя преломления, излучение с ростом z все более расплывается в поперечном направлении за счет перекачки мощности в периферийные световоды. Избежать такого расплывания можно в системе нелинейных световодов, к анализу которой мы и переходим.
Если амплитуды мод в соседних световодах достаточно близки, дискретное НУШ можно заменить его континуальным пределом классического НУШ. Соответствующее решение в виде светлого солитона имеет вид
An(z) = A0sch(Xn=w0) exp (i z + 2iCz);
где Xn = n — поперечная координата n-го световода, w0 >> — ширина дискретного солитона и sch(x) = 1=ch(x) — гиперболический секанс. Такой солитон отвечает возбуждению большого числа световодов. При отказе от континуального режима численное решение (2.29) показывает возможность формирования весьма узких (локализованных только на нескольких световодах) солитонов с нулевой или ненулевой компонентой скорости движения

2. Оптическое излучение... |
83 |
в поперечном направлении [75]. Для неподвижных солитонов известны два типа локализованных структур — четные и нечетные. Для четных структур максимум интенсивности достигается на двух соседних световодах и распределение поля (включая его фазу) симмметрично относительно средней координаты между этими световодами. Такие режимы оказываются неустойчивыми. Для нечетных структур максимум поля достигается только на одном световоде и разность фаз меняет знак при переходе через этот центральный световод, причем это устойчивые дискретные солитоны. Направление движения зависит от мощности излучения, что позволяет использовать дискретные солитоны для оптического переключения и управления направлением пучков (см., например, [79]). Ниже мы приведем численные результаты для систем связанных световодов с нелинейным усилением и поглощением, но сначала рассмотрим несколько иной подход, позволяющий более точно описать зонную структуру периодической системы световодов и подчеркивающий принадлежность дискретных систем к фотонным кристаллам [80].
Схема отвечает периодической системе тонкопленочных планарных нелинейных волноводов, вдоль оси которых z распространяется монохроматическое излучение с частотой !0. В направлении y волноводы считаются одномодовыми и соответствующая зависимость исключается так же, как в разделе 2.2. Исходным служит квазиоптическое уравнение для огибающей поля, которое в безразмерной форме имеет следующий вид:
i |
@A |
+ |
@2A |
+ F(I; x)A = 0: |
(2.33) |
||
@z |
|
|
@x2 |
||||
Здесь I = |A|2 — безразмерная интенсивность излучения, а вещественная функция F(I; x) описывает периодическое по поперечной координате линейное и квадратичное по амплитуде поля нелинейное изменение диэлектрической проницаемости среды. Для структур излучения с неизменным поперечным профилем можно положить A(x; z) = u(x) exp (i z), после чего (2.33) превращается в нелинейное уравнение Хилла
d2u |
+ F(I; x)u = u: |
(2.34) |
dx2 |
Приближение периодической (с периодом ) системы бесконечно тонких нелинейных слоев отвечает записи F(I; x) в форме суммы дельта-функций:
∞
∑
F(I; x) = |
( + I) (x − n ): |
(2.35) |
|
n=−∞ |
|
За счет нормировки интенсивности коэффициент = +1 для самофокусировочной нелинейности и = −1 для самодефокусировочной нелинейности. Соотношение (2.35) может быть уточнено за счет введения дополнительных линейных тонких слоев, промежуточных между нелинейными слоями [80].
Модель (2.34), (2.35) более точно, чем (2.29), описывает зонную структуру периодической системы и допускает приближенное аналитическое решение
84 |
Н.Н. Розанов |
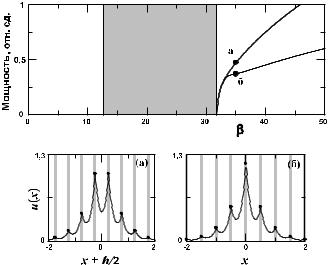
Рис. 2.12. Полная мощность в зависимости от постоянной распространения для нечетных (сплошная линия) и четных (штриховая линия) солитонов в самофокусировочной среде (сверху). Штриховка отмечает полосу пропускания. Внизу показаны профили интенсивности локализованных мод, отвечающие отмеченным точкам (а) и (б). Кружки представляют аналитическую аппроксимацию амплитуд в узлах [80].
в ряде предельных случаев [18]. На рис. 2.12 приведены примеры дискретных солитонов, получаемых в рамках этой модели для самофокусировочной нелинейности. Здесь четные структуры также оказываются неустойчивыми. Устойчивые нечетные солитоны отвечают нахождению частоты в запрещенной зоне, что обеспечивает локализацию (экспоненциальное убывание поля на периферии солитона).
Аналогичные структуры найдены и для самодефокусировочной нелинейности (рис. 2.13). Четные структуры здесь по-прежнему неустойчивы, а нечетные могут становиться неустойчивыми при превышении интенсивностью критического значения.
Если в однородной керровской среде связанные состояния солитонов невозможны, то в керровской среде с периодическим изменением такие состояния могут становиться устойчивыми. Они отвечают противофазной комбинации двух светлых дискретных солитонов и называются сцепленными модами. На рис. 2.14 и 2.15 показаны соответствующие результаты для случаев самофокусировочной и самодефокусировочной нелинейностей. Видно, что имеются широкие области устойчивости таких режимов, расположенные вне области пропускания. Неустойчивость (изображена пунктиром) может иметь колебательный характер.
Эксперименты по консервативным дискретным солитонам. Эксперименты выполнялись на материале AlGaAs [81], а также на полимерных материа-
2. Оптическое излучение... |
85 |
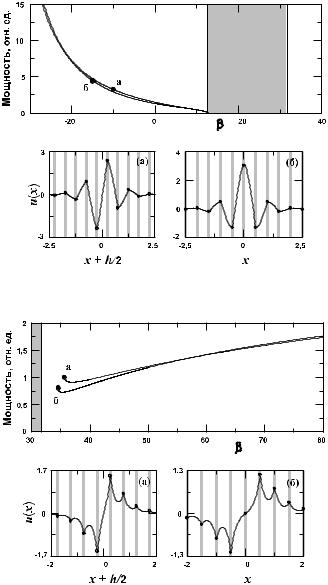
Рис. 2.13. То же, что на рис. 2.12, для среды с самодефокусировочной нелинейностью [80].
Рис. 2.14. Мощность солитона в зависимости от постоянной распространения для нечетных (сплошная линия) и четных (штриховая линия) сцепленных солитонов в самофокусировочной среде (сверху). Штриховка отмечает полосу пропускания. Внизу показаны профили амплитуды локализованных мод, отвечающих отмеченным точкам
(а) и (б) [80].

86 Н.Н. Розанов
Рис. 2.15. То же, что на рис. 2.14, для среды с нелинейностью самодефокусировочного типа [80].
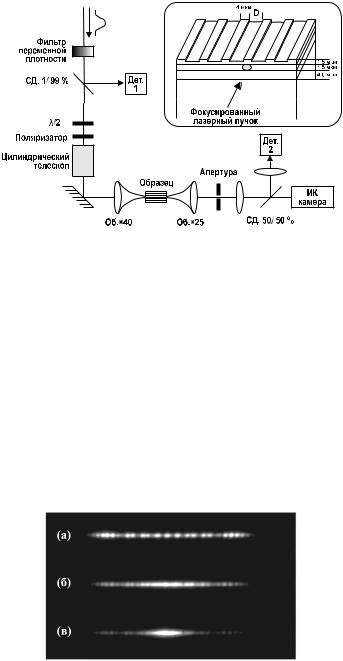
лах [74]. Схема установки показана на рис. 2.16. В экспериментах на основе AlGaAs система одномодовых волноводов шириной 4 мкм создавалась методом ионного травления. Система состояла из нескольких десятков волноводов с составом Al0;18Ga0;82As, разделенных оболочкой, включающей 24 % Al. Управление связью между соседними волноводами достигалось изменением расстояния между волноводами в диапазоне от 2 до 7 мкм. Схема всего волновода показана на вставке к рис. 2.16. Для формирования дискретных солитонов использовался синхронно накачиваемый оптический параметрический генератор. Он излучал импульсы длительностью от 100 до 200 фс, центральная длина волны которых перестраивалась в области 1.5 мкм. Максимально доступная пиковая мощность составляла 1.5 кВт.
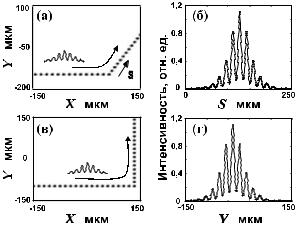
Входной пучок фокусировался в единственный волновод системы длиной 6 мм. Распределение интенсивности на выходе представлено на рис. 2.17 при трех уровнях входной мощности: 70, 320 и 500 Вт. При мощности 70 Вт распространение было практически линейным и пучок расширялся, охватывая более 30 волноводов (рис. 2.17а). Из этого распределения интенсивности можно найти коэффициент связи между волноводами. При возрастании мощности выходной пучок распространялся на несколько волноводов (рис. 2.17б), пока наконец не был максимально ограничен пятью волноводами в режиме дискретного солитона при мощности 500 Вт (рис. 2.17в). Эксперименты находятся в хорошем согласии с результатами расчетов.
Весьма перспективным представляется использование дискретных солитонов для обработки информации в двумерных сетях нелинейных волноводов, предложенное в работах [82, 83]. Такая сеть состоит из ряда ветвей, обра-
2. Оптическое излучение... |
87 |
Рис. 2.16. Экспериментальная установка для наблюдения дискретных солитонов. На вставке схематически показана конструкция волновода [81].
зованных идентичными регулярно расположенными одномодовыми световодами, разделенными расстоянием . В одной из ветвей сети возбуждается дискретный солитон, перекрывающий 5—7 световодов. Наложением наклона волнового фронта солитон можно заставить двигаться вдоль любой ветви сети. Существенным вопросом являются потери энергии солитона при резких изгибах световодов. Этот вопрос исследовался с помощью численного моделирования [82]; результаты для изгибов на 120 и 90 представлены на рис. 2.18. Потери при изгибах оказываются весьма малыми: (менее 0,7 % при угле изгиба 120 и 5 % при изгибе на 90 ). Более того, эти потери можно почти полностью устранить модификацией узлов соединения, внося в них соответствующий дефект [84]. В результате сигналы на основе дискретных солитонов могут практически без потерь перемещаться управляемым обра-
Рис. 2.17. Изображения выходной грани системы волноводов с длиной 6 мм с расстоянием между волноводами 4 мкм при входной пиковой мощности 70 (а), 320 (б) и 500 Вт (в) [81].
88 Н.Н. Розанов
,
, |
, |
, |
|
, |
, |
Рис. 2.18. a — дискретный солитон, распространяющийся вдоль 120-градусного изгиба; б — интенсивность солитона после прохождения изгиба; в — то же, что на а, но для 90-градусного изгиба; г — интенсивность солитона после изгиба вдоль вертикальной ветви [82].
зом по всей двумерной сети нелинейных волноводов. Недавние обзоры достигнутых результатов содержатся в [85, 86].
Еще одним перспективным направлением создания и применения дискретных солитонов служат волноводы, оптически наведенные в фоторефрактивных кристаллах [87]. Волноводы формируются в сильно анизотропном кристалле интерференцией нескольких плоских волн с поляризацией, отвечающей пренебрежимо слабой нелинейности, чтобы исключить нелинейные искажения создаваемых волноводов. Сигнальное излучение обладает поляризацией, отвечающей максимальной нелинейности; при этом оно подвержено и действию периодической модуляции показателя преломления, созданной интерферирующими плоскими волнами.
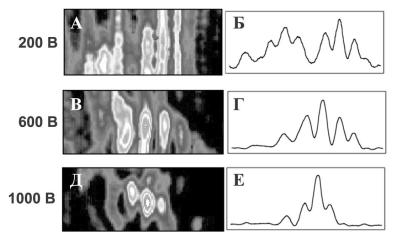
Экспериментально такая схема реализована в кристалле SBN длиной 6 мм, и результаты показаны на рис. 2.19. На входе лазерный пучок возбуждал один волновод. Уровень нелинейности регулировался внешним электрическим напряжением. При слабой нелинейности (напряжение 200 В) сигнальный пучок демонстрирует линейную дискретную дифракцию. Сильно локализованный дискретный солитон формировался при напряжении 1000 В, причем поля в соседних волноводах были противофазны.
Другой важный класс локализованных структур излучения представляют диссипативные дискретные солитоны. В [88] анализ таких структур, состоящих из слабо связанных одномодовых световодов с нелинейным усилением и поглощением, выполнялся с использованием модельной нелинейности третьей-пятой степени. Реалистичней представляется использование более стандартного вида насыщения нелинейности [19, 29], когда система управ-
2. Оптическое излучение... |
89 |
Рис. 2.19. Формирование дискретного солитона в оптически наведенной системе волноводов при усилении самофокусировочной нелинейности приложением внешнего электрического напряжения от 200 (А, Б) до 1000 В (Д, Е). Слева показаны фотографии выходной грани кристалла, справа — разрез соответствующих профилей интенсивности [87].
ляющих уравнений (2.29) заменяется следующей:
dAn |
+ An + C(An−1 + An+1) + f (|An|2)An = 0; |
||||||
i |
|
||||||
dz |
|||||||
где |
|
(−1 + 1 + |A|2 |
− 1 + b|A|2 ) |
: |
|||
f (|A|2) = |A|2 − i |
|||||||
|
|
|
|
g0 |
|
a0 |
|
При = 0 мы вновь получим случай керровской нелинейности и дискретное НУШ (2.29). Новыми параметрами являются a0 и g0 — коэффициенты линейного усиления и поглощения и b — отношение интенсивностей насыщения усиления и поглощения. При = 1 продольная координата z нормирована на длину нерезонансного поглощения.
На представленных ниже рисунках распределения интенсивностей и фаз мод в зависимости от номера солитона N соединены для удобства сплошными линиями. Прежде всего, отметим специфику волн переключения в периодических системах. Под волной переключения мы будем понимать пространственно-неоднородное распределение типа фронта, типичное для широкого круга оптических бистабильных систем [19, 25]. В обычных (однородных) бистабильных системах скорость фронта волны переключения является знакопеременной функцией контрольного параметра, например коэффициента усиления, обращающейся в нуль при одном (“максвелловском”) его значении [25]. Однако это не так в периодически неоднородных системах, в которых скорость волны переключения обращается в нуль в целом диапазоне
