
- •1. Фотонные кристаллы
- •1.1. Концепция
- •1.1.1. Электроны в кристаллических структурах
- •1.1.2. Электромагнитные волны в кристаллических структурах
- •1.1.3. Фотонное твердое тело: распространение и локализация электромагнитных волн в условиях сильного многократного рассеяния
- •1.2. Синтез и свойства фотонных кристаллов
- •1.2.1. Фотонные кристаллы в природе
- •1.2.2. Одномерные периодические структуры
- •1.2.3. Двумерные периодические структуры
- •1.2.4. Трехмерные периодические структуры
- •1.3. Испускание и рассеяние излучения в фотонных кристаллах: роль плотности фотонных состояний
- •1.3.1. Интегральная и локальная плотности состояний
- •1.3.2. Спонтанное испускание фотонов
- •1.3.3. Тепловое излучение
- •1.3.4. Комбинационное рассеяние
- •1.3.5. Резонансное (релеевское) рассеяние
- •1.4. Заключение
- •Список литературы
- •2. Оптическое излучение в линейных и нелинейных периодических структурах
- •2.1. Введение
- •2.2.1. Квазиоптическое приближение
- •2.2.2. Линзовые волноводы и лазерные резонаторы
- •2.2.4. Мелкомасштабная самофокусировка в периодических системах
- •2.2.5. Квазисинхронное параметрическое взаимодействие
- •2.3. Одномодовый световод с брэгговской решеткой
- •2.3.1. Двунаправленное распространение излучения
- •2.3.2. Брэгговские солитоны
- •2.3.3. Оптическая бистабильность и переключение
- •2.3.4. Полупроводниковые микрорезонаторы
- •2.4. Связанные световоды
- •2.5. Двумерные фотонные кристаллы
- •2.5.1. Неидеальные фотонные кристаллы
- •2.5.2. Нелинейные двумерные фотонные кристаллы
- •2.6. Заключение
- •Список литературы
- •3. Оптика квантовых ям и сверхрешеток
- •3.1. Классификация гетероструктур
- •3.2. Размерное квантование электронных состояний
- •3.3. Правила отбора при оптических переходах
- •3.3.1. Междузонные и внутризонные оптические переходы между подзонами размерного квантования
- •3.3.2. Поляризационные свойства оптических переходов из подзон тяжелых и легких дырок
- •3.4. Резонансное отражение и поглощение света в структурах с квантовыми ямами
- •3.5. Вторичное свечение гетероструктур
- •3.6. Квантовые микрорезонаторы
- •3.7. Заключение
- •Список литературы
- •4. Оптика квантовых точек
- •4.1. Введение
- •4.1.1. Состояния размерного квантования электронных и фононных возбуждений квантовых точек
- •4.1.2. Электрон-фононное взаимодействие в квантовых точках
- •4.1.3. Динамика электронных возбуждений квантовой точки
- •4.2. Оптические методы исследования квантовых точек
- •4.2.1. Изучение энергетической структуры электронных возбуждений
- •4.2.3. Исследование динамики элементарных возбуждений квантовых точек
- •4.2.4. Оптическая спектроскопия одной квантовой точки
- •4.3. Применение квантовых точек
- •4.3.1. Лазеры на квантовых точках для волоконной связи
- •4.3.2. Квантовые точки в биологии и медицине
- •Список литературы
- •5. Оптические резонансные свойства металлических наночастиц
- •5.1. Введение
- •5.2. Резонансы Ми отдельных металлических наночастиц
- •5.2.1. Эффект размера
- •5.2.2. Эффекты формы
- •5.3. Действие окружения на резонансы металлических наночастиц
- •5.3.1. Электродинамические эффекты
- •5.3.2. Контактные эффекты
- •5.4. Нелинейные оптические свойства металлических наночастиц
- •5.4.1. Генерация высших гармоник
- •5.4.2. Оптические комбинационные процессы
- •5.5. Неоднородные системы металлических наночастиц
- •5.5.1. Структурные параметры неоднородных систем
- •5.5.2. Измерение релаксационных параметров индивидуальных резонансов в неоднородных системах
- •5.6. Применения металлических наночастиц, связанные с их оптическими свойствами
- •5.7. Заключение
- •Список литературы

2. Оптическое излучение... |
73 |
2.3.2. Брэгговские солитоны
Одним из важнейших следствий нелинейности уравнений связанных волн (2.16) служит наличие их локализованных (солитоноподобных) решений, которые имеют вид [53]
|
|
|
|
|
|
|
Af (z; t) = a+sch( − i |
=2)ei ; |
|
|
|
|
|
|
(2.20) |
|||||||||||
где |
|
|
|
|
Ab(z; t) = a−sch( + i |
=2)ei ; |
|
|
|
|
|
|
(2.21) |
|||||||||||||
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
a± = ± 1 |
± v |
|
|
(3 |
− v2) sin ; = √− |
G |
|
2 |
sin |
; |
|
(2.22) |
||||||||||||||
|
1 |
v |
|
1=4 |
|
|
|
(1 |
v2) |
|
z V t |
|
|
|
|
|||||||||||
( |
|
|
|
|
) |
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
1 − v |
|
|
|
|
|
|||||||||||
= |
v(z − VGt) |
|
|
|
|
4v |
|
|
|
|
= |
|
|
: |
(2.23) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
√ |
1 − v2 |
|
|
|
cos − (3 − v2) arctg[|ctg( |
|
|
|
2)|cth |
] |
|
|
|||||||||||
Согласно (2.20)–(2.23), семейство брэгговских солитонов двухпараметрическое. Параметр v меняется в диапазоне −1 < v < 1, а параметр выбирается в диапазоне 0 < < . Частный случай = =2, отвечающий центру запрещенной зоны, первоначально был изучен в [56]. Брэгговские солитоны отвечают таким комбинациям встречных волн, огибающие которых движутся вместе с уменьшенной скоростью VG = vvg. Так как параметр v может быть и отрицательным, солитон огибающих может двигаться вперед или назад. Если доминирует Af (Ab), солитон движется в прямом (встречном) направлении с уменьшенной скоростью. В случае равных амплитуд солитон неподвижен, VG = 0 (случай стационарных щелевых солитонов). В пределе |v| → 1 брэгговские солитоны отсутствуют. Длительность солитона Ts связана с параметрами v и и определяется выражением
√
Ts = 1 − v2=( VG sin ):
Брэгговские (щелевые) солитоны с аналитическим видом огибающих (2.20) и (2.21) входят в более общий класс солитонов, который может быть найден численным решением нелинейных уравнений связанных мод (2.16) при требовании сохранения формы солитона при распространении [58, 59]. Такие локализованные решения существуют и внутри, и вне запрещенной зоны для фокусирующей и дефокусирующей нелинейностей. При сравнительно малых нелинейностях уравнения связанных мод сводятся к эффективному нелинейному уравнению Шредингера (НУШ), солитоны которого хорошо изучены. Анализ подтверждает устойчивость щелевых солитонов в сравнительно широкой области параметров [60]. При взаимодействии с дефектами решетки щелевые солитоны ведут себя подобно классическим частицам, так что в зависимости от параметров возможны захват, отражение и прохождение щелевых солитонов [61].
Экспериментально брэгговские солитоны в световодах с наведенной решеткой впервые обнаружены в 1996 г. [63]. В типичных условиях такие солитоны наблюдались в аподизированном световоде с решеткой длиной 7.5 см.
74 Н.Н. Розанов
,
, |
, |
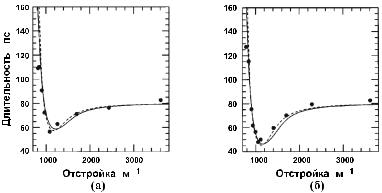
Рис. 2.5. Экспериментальные зависимости длительности импульсов на выходе решетки (кружки) от отстройки для входных импульсов длительности 80 пс с пиковой интенсивностью 3 (а) и 6 ГВт/см2 (б). Сплошные и штриховые линии показывают соответственно результаты расчетов в рамках теории связанных мод и эффективного НУШ [62].
Входные импульсы длительностью 80 пс получались из импульсов Nd:YLFлазера в режиме модулированной добротности и синхронизации мод (длина волны 1053 нм) с пиковой интенсивностью около 10 ГВт/см2. Результаты, естественно, сильно зависят от отстройки от брэгговского резонанса. На рис. 2.5 представлены экспериментальные (черные кружки) и расчетные (сплошные линии — уравнения связанных волн, штриховые линии — эффективное НУШ) зависимости длительности импульса на выходе решетки от расстройки при длительности входного импульса 80 пс и двух значениях пиковой интенсивности. Результаты подтверждают справедливость эффективного НУШ в области его применимости. Практически возбуждение щелевых солитонов внутри запрещенной полосы затруднительно из-за отражения света в этой области при введении в решетку излучения. Решение этой проблемы возможно при использовании эффекта вынужденного комбинационного рассеяния света, когда импульс накачки с частотой вне запрещенной зоны возбуждает в самой решетке комбинационный щелевой солитон [64].
2.3.3. Оптическая бистабильность и переключение
Другим важным нелинейным эффектом, реализующимся в брэгговских решетках, является оптическая бистабильность, т.е. двузначная зависимость мощности прошедшего решетку излучения от мощности падающего излучения. Этот эффект можно найти решением уравнений связанных волн (2.16) в стационарном случае при соответствующих граничных условиях на двух концах решетки (z = 0 и z = L), причем решение выражается через эллиптические функции [65]. Характерные зависимости показаны на рис. 2.6. Видно, что бистабильность реализуется при превышении отстройкой определенного
2. Оптическое излучение... |
75 |
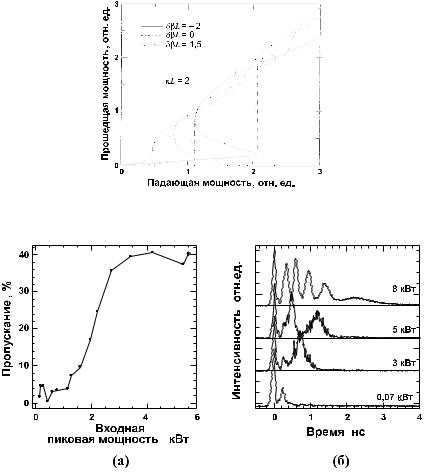
Рис. 2.6. Прошедшая мощность в зависимости от падающей мощности для трех зна- |
|
чений отстройки внутри запрещенной зоны [65]. |
|
, |
|
, |
, |
|
|
Рис. 2.7. Пропускание в зависимости от пиковой мощности на входе, демонстрирую- |
|
щее нелинейное переключение (а); форма импульсов на выходе при нескольких уров- |
|
нях пиковой мощности входного импульса (б) [67]. |
|
критического значения. Качественно эффект можно пояснить, заметив, что эффективная отстройка в нелинейной решетке зависит от интенсивности излучения. При низких интенсивностях (линейный режим) входное излучение с частотой внутри запрещенной зоны отражается от решетки, практически не проникая в нее. Однако при достаточно больших интенсивностях из-за нелинейного сдвига отстройки большая´ часть излучения проходит через решетку. Более детальные расчеты показывают, что часть верхней ветви при больших интенсивностях становится неустойчивой. Тогда при монохроматическом входном излучении выходное излучение характеризуется периодической или даже хаотической зависимостью от времени [66].

76 |
Н.Н. Розанов |
|
, |
|
, |
|
, |
|
, |
Рис. 2.8. Зависимость пропускания решетки от пиковой мощности на входе, демон- |
|
стрирующая действие И-вентиля (а), и форма импульса на выходе при уровне пиковой |
|
мощности 3 кВт, когда на вход подана только одна (штриховая линия) или обе (сплош- |
|
ная кривая) поляризационные компоненты (б) [67]. |
|
Как видно из рис. 2.6, выбором отстройки можно достичь и другого нелинейного режима — оптического переключения, характеризующегося резкой зависимостью пропускания от интенсивности входного сигнала. Экспериментально нелинейное переключение в световоде с брэгговской решеткой впервые наблюдалось в 1998 г. в важной для волоконно-оптической связи области длин волн 1.55 мкм [67, 68]. В эксперименте использовалась решетка длиной 8 см с максимальным коэффициентом отражения 98 %. Входные импульсы обладали длительностью 3 нс и пиковой мощностью до 10 кВт. На рис. 2.7а виден резкий рост пропускания до 40 % при увеличении мощности до 3– 4 кВт. На рис. 2.7б показаны временные´ профили излучения на выходе при различных мощностях. Формирование нескольких импульсов при больших мощностях связано с упомянутой выше неустойчивостью непрерывного режима.
В световоде с двулучепреломлением компоненты моды с ортогональными поляризациями обладают различными показателями преломления. Запрещенные зоны для этих поляризаций несколько сдвинуты друг относительно друга. Нелинейный сдвиг запрещенных зон также различен для двух поляризаций. При сравнительно малых интенсивностях (предел эффективных НУШ) режимы описываются двумя связанными уравнениями вида [69]
@Ax |
|
|
i 2g @2Ax |
|
|
2 |
|
2 |
|
|
|
2 |
|
i g |
|
|
2 |
2i z |
|
|
|
|||||||||
|
|
+ |
|
|
|
|
|
|
|
|
= i g (|Ax| |
|
+ |
|
|Ay| |
) |
Ax |
+ |
|
A*xAy e− |
|
|
; |
|
(2.24) |
|||||
@z |
|
|
2 |
|
|
@t2 |
|
|
3 |
3 |
|
|
|
|||||||||||||||||
|
@Ay |
|
|
|
i 2g @2Ay |
= i g (|Ay|2 + |
2 |
|Ax|2) |
|
|
i g |
|
2 |
2i z |
|
|
||||||||||||||
|
|
|
|
+ |
|
|
|
|
|
|
Ay + |
|
|
Ay*Axe |
|
|
; |
(2.25) |
||||||||||||
|
|
@z |
|
|
2 |
|
|
@t2 |
3 |
|
3 |
|
|
|||||||||||||||||
2. Оптическое излучение... |
77 |
где ≡ 0x − 0y — разность постоянных распространения для ортогональных поляризаций. Эти уравнения имеют решение в виде векторного солитона с равными амплитудами, или связанного щелевого солитона [69].
Связанный щелевой солитон можно использовать для построения чисто оптического И-вентиля. Поляризационные x- и y-компоненты входного излучения служат единицами информации — битами, каждый из которых принимает значение 0 или 1 в зависимости от отсутствия или присутствия соответствующего сигнала. Для вентиля И необходимо, чтобы выходной импульс появлялся, только если присутствуют одновременно обе компоненты. Для этого нужно, чтобы обе поляризационные компоненты отвечали запрещенной зоне. Их суммарная интенсивность может настолько увеличить эффективный показатель преломления, что обе компоненты будут пропущены. Однако, если хотя бы одна из компонент на входе отсутствует (0 бит), обе компоненты отражаются решеткой. В эксперименте такой чисто оптический И-вентиль был реализован в 1988 г., причем был получен контраст переключения 17 дБ при пиковой мощности 2.5 кВт [70]. На рис. 2.8 показана доля прошедшей энергии по отношению к полной энергии импульса в зависимости от пиковой мощности на входе (а) и форма прошедшего импульса при пиковой мощности 3 кВт (б). Когда на вход подается только одна поляризационная компонента, решетка пропускает малую часть энергии. Однако, когда подаются обе поляризационные компоненты, на выходе решетки наблюдается интенсивный импульс в соответствии с результатами расчетов на основе связанных НУШ (2.24) и (2.25).
Детальный теоретический и численный анализ нелинейного распространения излучения в одномерных периодических структурах, ориентированный на приложения к световодам с брэгговской решеткой, выполнен в [71], где изучены такие вопросы, как применимость квазиоптического приближения и метода связанных волн, инерционность отклика нелинейной среды и т.д. Впрочем, полнота этого весьма математизированного анализа вряд ли всесторонняя. В частности, задача здесь сразу считается одномерной, что оставляет нерешенным еще недостаточно изученный вопрос о поперечных эффектах в рассматриваемом световоде (поперечная структура излучения, во-первых, искажается из-за нелинейности среды и, во-вторых, различна для волн различных порядков). Еще более принципиальными представляются эффекты непараксиальности, связанные с ограниченностью параксиального приближения — приближения медленно меняющихся амплитуд. Рассмотрим, например, важный частный случай неподвижного брэгговского солитона. В рамках этого приближения, отвечающего уравнениям (2.16) при @=@t = 0, решение обладает инвариантностью к сдвигу по оси z на любую величину, т.е. расположение солитона никак не привязано к решетке показателя преломления. Между тем очевидно, что различные положения солитона физически далеко не эквивалентны, и более точные решения должны обладать симметрией только по отношению к сдвигу по оси z на период решетки. Такие решения можно получить из (2.3) для одномерной геометрии нелинейного уравнения
78 Н.Н. Розанов
Гельмгольца для вещественной амплитуды монохроматического поля с фиксированной поляризацией излучения
d2E |
+ |
!2 |
["0 + "1 cos (2 Bz) + "2E2 |
]E = 0: |
(2.26) |
|
dz2 |
|
c2 |
||||
|
|
|
|
|
||
Здесь коэффициент "1 отвечает (малой) глубине модуляции линейной диэлектрической проницаемости, а "2 пропорционален коэффициенту керровской нелинейности. Для справедливости (2.26) в среде с кубичной нелинейностью необходимо, чтобы амплитуда третьей оптической гармоники (с частотой 3!) была пренебрежимо мала (условия синхронизма на этой частоте не выполнены).
Будем искать решение уравнения (2.26) методом теории возмущений в виде
E(z) = E0(z − z0) + E(z);
где E0(z − z0) — приведенное выше решение в (нулевом) приближении медленно меняющихся амплитуд, z0 — подлежащая определению постоянная, отвечающая координате центра солитона, а E(z) — малая поправка к приближенному решению. Линеаризованное по E(z) уравнение (2.26) имеет вид
|
d2 E !2 |
|
|
|
|
|
||||
|
|
+ |
|
|
["0 + "1 cos (2 Bz) + 3"2E02] E = −R(z); |
(2.27) |
||||
|
dz2 |
|
c2 |
|||||||
где в правой части стоит известная из нулевого приближения величина |
|
|||||||||
|
|
|
d2E0 |
|
!2 |
["0 + "1 cos (2 Bz) + "2E02]E0: |
|
|||
|
R(z) = |
|
+ |
|
|
|
||||
|
dz2 |
|
c2 |
|
||||||
|
|
|
|
|
|
|
|
|||
Как известно, условием разрешимости неоднородного линейного уравнения (2.27) служит ортогональность его правой части R(z) решениям отвечающего (2.27) однородного уравнения E0(z) (однородное уравнение самосопряженное) Z
R(z) E0(z) dz = 0: (2.28)
Вид функции E0(z) может быть найден решением (2.27) в приближении медленно меняющихся амплитуд. Тем самым уравнение (2.28) позволяет найти координату центра солитона z0. Решение не может быть единственным, так как (2.28) сохраняется при сдвиге z0 на период решетки. Поэтому (2.28) дает дискретный и периодический (с периодом решетки) набор равновесных положений солитона, причем для чередующихся решений естественно полагать чередование устойчивости. Родственные рассуждения приложимы и к случаю движущихся брэгговских солитонов, причем здесь выявляется непараксиальный механизм потерь энергии солитона, связанный с движением. В строгом смысле слова устойчивые консервативные брэгговские солитоны неподвижны, тогда как диссипативные солитоны в решетках могут двигаться из-за компенсации потерь усилением.
