- •2. Первый закон Ньютона. Инерциальные системы отсчета. Принцип относительности Галилея. Преобразования Галилея. Второй и третий законы Ньютона.
- •3. Центр масс механической системы. Закон движения центра масс. Движение центра масс замкнутой системы. Закон сохранения импульса.
- •4. Работа силы и ее выражение через криволинейный интеграл. Мощность.
- •5.Кинетическая энергия системы. Связь изменения кинетической энергии и работы.
- •6.Консервативные и неконсервативные силы. Сила тяжести, сила упругости, центральные силы как консервативные силы.
- •8.Полная механическая энергия системы, связь её изменения с работой неконсервативных сил. Закон сохранения полной механической энергии.
- •9. Абсолютно неупругий удар. Абсолютно упругий удар. Скорости шаров после абсолютно упругого центрального удара.
- •Момент инерции
- •11.Основные уравнения динамики вращательного движения твердого тела.
- •12. Кинетическая энергия вращающегося твердого тела. Работа сил при вращательном движении тела. Кинетическая энергия твердого тела при плоском движении.
- •Кинетическая энергия при плоском движении
- •13.Гироскоп.Вывод формулы частоты прецессии гироскопа.
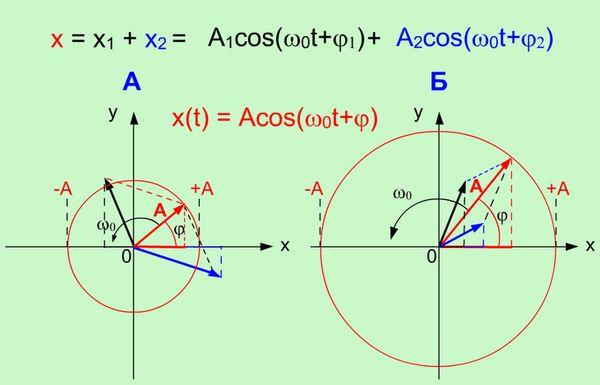
- •15.Сложение двух гармонических колебаний одинакового направления и частоты. Геометрическая интерпретация.
- •16.Дифференциальное уравнение затухающих колебаний и его решение. Основные характеристики затухающих колебаний. Логарифмический декремент затухания. Апериодический процесс.
- •17.Дифференциальное уравнение вынужденных колебаний и его решение. Резонанс. Резонансные кривые.
13.Гироскоп.Вывод формулы частоты прецессии гироскопа.
Гироскоп - устройство, способное реагировать на изменение углов ориентации тела, на котором оно установлено в ИнСиОт. Вывод: M=L/t (М-момент силы); (am / JΩ) g; - маховик гироскопа будет совершать медленное вращение (прецессию) в горизонтальной плоскостиΩ L=JΩ( Ω– угловая частота); М = [a, F]; F=mg; L/t = [Ω, L]; [ωo, JΩ] = - [mg, a];
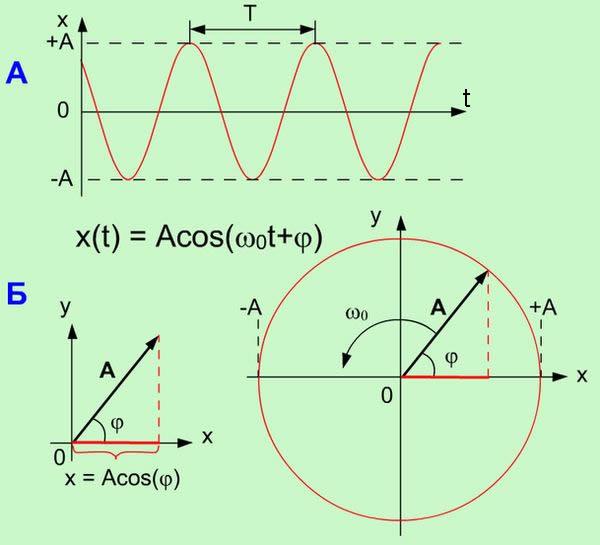
14.дифференциальное уравнение гармонических колебаний и его решение. Основные характеристики гармонических колебаний. Векторное изображение колебаний. Гармонические колебания груза на пружине, математического и физического маятников. Энергия гармонических колебаний(на примере пружинного маятника) Графики зависимости смещения, скорости, ускорения, кинетической и потенциальной энергии колебаний от времени.
(d^2)s/d(t^2)+ωs=0; (d^2)s/d(t^2)= -A (ω^2)(sin^2 )(ωt+φ); ds/dt= Acosx(ωt+φ); s(t)=Asinx(ωt+φ)-уравнение гармонических колебаний. Колебания вдоль оси х. Бывают свободные и вынужденные. Для расчета Гарм.колеб обычно рассматривают плоскость векторного изображения как комплексную плоскость с вращающемся вектором А, c соотношением z=A(cos ωt+isin ωt)
15.Сложение двух гармонических колебаний одинакового направления и частоты. Геометрическая интерпретация.
При
сложении двух гармонических колебаний
одинакового направления и частоты,
результирующее смещение будет суммой
(![]() )
смещений
)
смещений ![]() и
и ![]() ,
которые запишутся следующими выражениями:
,
которые запишутся следующими выражениями:
![]() ,
, ![]() ,
Сумма
двух гармонических колебаний также
будет гармоническим колебанием той же
круговой частоты:
,
Сумма
двух гармонических колебаний также
будет гармоническим колебанием той же
круговой частоты:
![]() =
= ![]() .
Значения
амплитуды А и начальной фазы φ этого
гармонического колебания будет зависеть
от амплитуд исходных колебаний и их
начальных фаз (Рис. 1.2).
.
Значения
амплитуды А и начальной фазы φ этого
гармонического колебания будет зависеть
от амплитуд исходных колебаний и их
начальных фаз (Рис. 1.2).
|
|
|
Рисунок 1.2. Сложение двух гармонических колебаний одинакового направления и частоты |
На
рисунке 1.2. приведено два примера А и В
сложения гармонических колебаний с
использованием метода
векторных диаграмм. Из
векторных диаграмм видно, что направление
(начальная фаза φ)
и длина А вектора амплитуды суммарного
гармонического колебания зависит, как
от направления (от начальных фаз), так
и от длины векторов амплитуд исходных
гармонических колебаний.
Если
угол (разность фаз:
Δφ = φ1 - φ2)
между векторами А1 и А2 равен
0, то исходные колебания находятся
в фазе и
суммарная амплитуда (А =А1 +А2)
будет максимальна. Если угол (разность
фаз: Δφ = φ1 - φ2)
между векторами А1 и А2 равен
- π или π, то исходные колебания находятся
в противофазе и
суммарная амплитуда (А = ![]() А1 -А2
А1 -А2![]() )
будет минимальна.
)
будет минимальна.
16.Дифференциальное уравнение затухающих колебаний и его решение. Основные характеристики затухающих колебаний. Логарифмический декремент затухания. Апериодический процесс.
будем
считать, что наряду с упругой или
квазиупругой силой Fy в
системе действует сила трения,
пропорциональная скорости и направленная
противоположно ей: Fтр = ![]() .
Тогда учет влияния этих двух сил на
характер движения приводит к следующему
дифференциальному уравнению:
.
Тогда учет влияния этих двух сил на
характер движения приводит к следующему
дифференциальному уравнению:
![]() 8)
8)
Разделив левую и правую части уравнения (8) на m ,обозначив r/m = 2b и сохранив обозначение к/m = w02 , приведем это уравнение к виду:
![]() (9)
(9)
Решение этого уравнения имеет вид:
![]() (10)
(10)
Формула (10) представляет собой смещение при затухающем колебании как функцию времени и параметров системы b и w. Коэффициент b = r/2m имеет смысл коэффициента затухания. Из формулы (10) видно, что в затухающих колебаниях амплитуда уменьшается со временем. Причем, колебания затухают тем быстрее, чем больше коэффициент затухания b. По сравнению с гармоническими колебаниями уменьшается также и циклическая частота колебаний w. Это уменьшение зависит от коэффициента затухания. Оказывается, что
![]() (11)
(11)
Колебательный процесс может происходить лишь при условии: (w02 - b 2)>0, когда частота w в формуле (11) является действительной величиной . Если же затухание в системе слишком велико (w0 < b ) , то под корнем в формуле (11) оказывается отрицательная величина, - в этом случае движение не имеет периодического характера.
Графически затухающее колебания представлено на рис.2, где сплошной линией показана зависимость смещения от времени, а пунктирной - экспоненциальный закон убывания амплитуды.
что быстрота убывания амплитуды затухающих колебаний характеризуется коэффициентом затухания b , который зависит от параметров системы. На практике затухание колебаний удобнее характеризовать декрементом затухания d , представляющим собой отношение двух последовательных амплитуд, разделенных периодом колебаний Т (см. рис.2) :
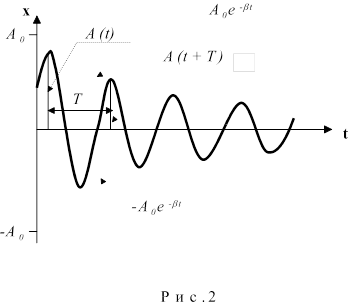
Натуральный логарифм этого отношения, называемыйлогарифмическим декрементом затуханияl, весьма просто связан с коэффициентом затухания и периодом:
 или l
= bT . (12)
или l
= bT . (12)
Удобство использования логарифмического декремента затухания l для характеристики затухающих колебаний заключается в простоте его экспериментального определения. Если затухающие колебания зарегистрированы в виде соответствующего графика (см.рис.2), то необходимо в любых единицах измерить две амплитуды колебаний, разделенные интервалом времени, равным периоду, и найти натуральный логарифм их отношения. Определив таким образом величину l и зная период Т , легко найти и коэффициент затухания b .
Для характеристики качества колебательной системы вводится ряд параметров:
- время релаксации затухающих колебаний (за амплитуда уменьшается в e раз).
![]() - логарифмический
декремент затухания; N -
число колебаний, в течение которых
амплитуда уменьшается в eраз.
Соответственно, exp()
- просто декремент
затухания.
- логарифмический
декремент затухания; N -
число колебаний, в течение которых
амплитуда уменьшается в eраз.
Соответственно, exp()
- просто декремент
затухания.
![]() - добротность
колебательной системы; W(t)
- энергия (полная) колебательной системы
в момент времени t.
- добротность
колебательной системы; W(t)
- энергия (полная) колебательной системы
в момент времени t.