Момент инерции

Моментом инерции системы (тела) относительно данной оси называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:  В случае непрерывного распределения масс эта сумма сводится к интегралу  где интегрирование производится по всему объему тела. При этом величина r в есть функция положения точки с координатами х, у, z. В качестве примера будем искать момент инерции однородного сплошного цилиндра высотой h и радиусом R относительно его геометрической оси (рис. 1). 

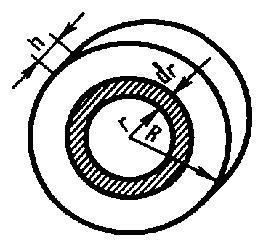
Рис.1

Разобьем цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом r и внешним r+dr. Момент инерции отдельного полого цилиндра dJ=r²dm (так как dr<<r, то считаем, что расстояние всех точек цилиндра от оси равно r), где dm - масса всего элементарного цилиндра; его объем 2πrhdr. Если ρ-плотность материала, то dm=2πrhρdr и dJ=2πhρr³dr. Тогда момент инерции сплошного цилиндра  но так как πR2h - объем цилиндра, то его масса m=πR2hρ, а момент инерции  Если мы знаем момент инерции тела относительно оси, проходящей через его центр масс, то мы можем найти и момент инерции относительно любой другой параллельной этой оси, который можно найти с помощью теоремы Гюйгенса-Штейнера: момент инерции тела J относительно произвольной оси равен моменту его инерции J_c относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния а между осями:  Приведем значения моментов инерции (табл. 1) для некоторых тел (тела считаются однородными, m - масса тела).

11.Основные уравнения динамики вращательного движения твердого тела.

Основной закон динамики вращательного движения можно получить из второго закона Ньютона для поступательного движения твердого тела

  ,                                                                                                       (1.6)

где F – сила, приложенная к телу массой m; а – линейное ускорение тела.

Если к твердому телу массой m в точке А (рис. 5) приложить силу F, то в результате жесткой связи между всеми материальными точками тела все они получат угловое ускорение и соответственные линейные ускорения, как если бы на каждую точку действовала сила . Для каждой материальной точки можно записать:

,

где ,  поэтому

,                                                                                                  (1.7)

где m_i – масса i-й точки; – угловое ускорение; r_i – ее расстояние до оси вращения.

Умножая левую и правую части уравнения (1.7) на r_i, получают

,                                                                                               (1.8)

где – момент силы – это произведение силы  на ее плечо .

Плечом силы называют кратчайшее расстояние от оси вращения “ОО” (рис. 5) до линии действия силы .

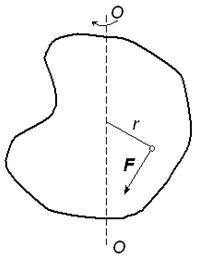
Рис. 5. Твердое тело, вращающееся под

действием силы F около оси “ОО”

– момент инерции i-й материальной точки.

Выражение (1.8) можно записать так:

.                                                                                                            (1.9)

Просуммируем левую и правую части (1.9) по всем точкам тела:

.

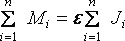Обозначим 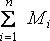через М, а через J, тогда

                                                                                                         (1.10)

Уравнение (1.10) – основной закон динамики вращательного движения твердого тела. Величина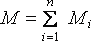– геометрическая сумма всех моментов сил, то есть момент силы F, сообщающий всем точкам тела ускорение .– алгебраическая сумма моментов инерции всех точек тела. Закон формулируется так: «Момент силы, действующий на вращающееся тело, равен произведению момента инерции тела на угловое ускорение».

Мгновенное значение углового ускорения , есть первая производная угловой скорости по времени , то есть

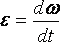,                                                                                                        (1.11)

где – элементарное изменение угловой скорости тела за элементарный промежуток времени .

Если в выражение основного закона (1.10) поставить значение мгновенного ускорения (1.11), то

    или        ,        (1.12)

где – импульс момента силы – это произведение момента силы  на промежуток времени .

– изменение момента импульса тела,  – момент импульса тела есть произведение момента инерции J на угловую скорость , а есть .

Поэтому основной закон динамики вращательного движения твердого тела формулируется так: “Импульс момента силы , действующий на вращательное тело, равен изменению его момента импульса ”:

   или