Глава III.

ЛИНИИ, ПОВЕРХНОСТИ И ИХ УРАВНЕНИЯ.

ЛЕКЦИЯ 1

I. ЛИНИЯ И ЕЕ УРАВНЕНИЯ.

§ 21. О понятии линии и ее уравнениях.

Определение I. Уравнением линии в декартовой системе коор­динат называется уравнение F(x,y)=0, (1) (это неявное уравнение линии) которому удовлетворяют координаты х, у всех точек этой линии и только координаты таких точек.

В частности, уравнение линии может иметь вид y=f(x) (явное уравнение) (2).

Уравнением линии в полярной системе координат называется уравнение (3), (это тоже неявное уравнение) которому удовлетворяют полярные координаты ивсех точек этой линии и только координаты таких точек.

В частности, уравнение линии в полярных ко-ординатах может иметь вид (явное) (4).

Определение II. Параметрическими уравнениями линии в де­картовой системе координат называются уравнения вида , где функции x(t) и у(t) имеют одну и ту же область определения, каждому значению t из этой области соответствует точка M(x(t),y(t)) рассматриваемой линии и каждая точка М этой линии соответствует некоторому значению t из области определе­ния функций x(t) и y(t), т. е. для любой точки М линии найдет­ся такое значение t, что x(t) и y(t) будут координатами точки М. Аналогично определяются параметрические уравнения линии в полярных координатах.

§ 22. Примеры составления уравнений линии.

Пример 1. Рассмотрим окружность S радиуса r с центром в точке C(a,b) заданной относительно декартовой прямоугольной системы координат (рис. 46) Пусть М(x,y) - произвольная точка плоскости. Точка М лежит на окружности

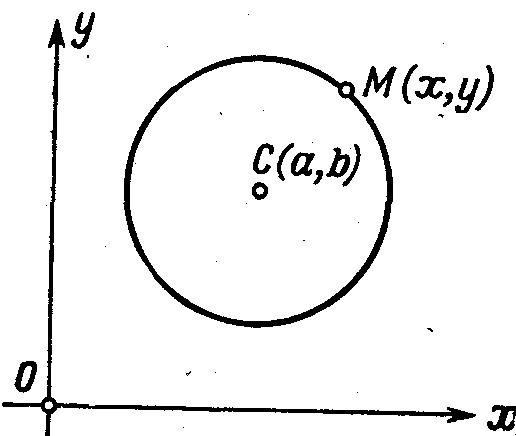рис. 46

рис. 47

S тогда и только тогда, когда расстояние между точками М и С равно радиусу r окружности S.

Расстояние между точками М и С равно 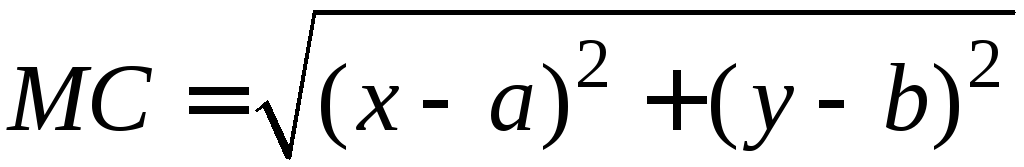,поэтому уравнение окружностиS имеет вид 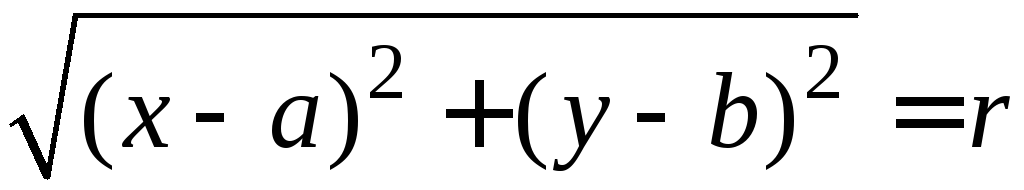, или (1), или(1').

В частности, уравнение окружности радиуса r с центром в начале коор­динат имеет вид (рис.47) ; (2),(2').

Уравнения (1') и (2') называются нормальными уравнением окружности.

Пример 2. Составить уравнение линии, произведение расстояний любой точки которой до двух данных точек F₁ и F₂ равно данному числу b².

Решение. Пусть расстояние между точками F₁ и F₂ равно 2а. За на­чало О декартовой прямоугольной системы координат на плоскости примем середину отрезка F₁F₂ , а прямую F₁F₂ с положительным направлением от О к F₂ примем за ось Ох. Точка F₁ в выбранной системе координат имеет коорди­наты: (-а,0), а точка F₂ - (а,0). Согласно условию задачи или . Применяя формулу расстояния между двумя точками, находим, и соотношение принимает вид:

,

Линии, определяемые этим уравнением, называются овалами Кассини. Изображения их (для случаев a>b , а=b, а < b) даны на рис. 48. Если а=b,

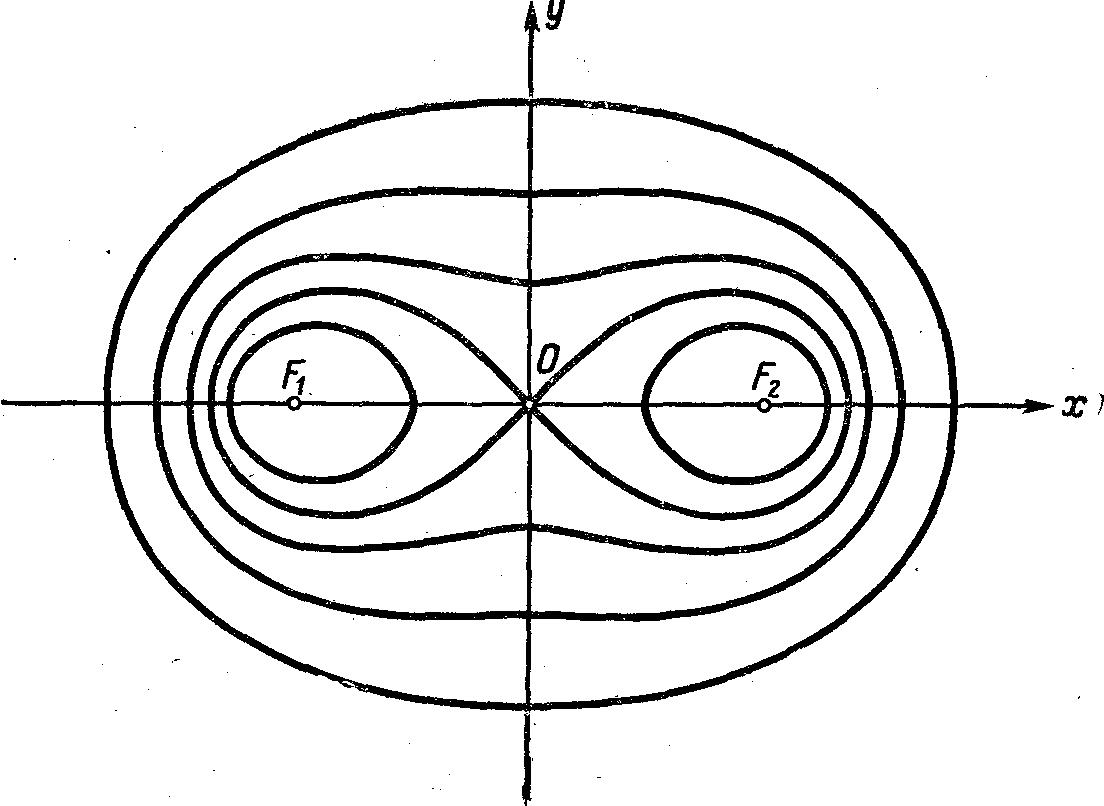
Рис. 48

т. е. если произведение расстояний от точки М до точек F₁ и F₂, равно квадрату половины расстояния между точками F₁ и F₂, то овал Кассини называется лемнискатой Бернулли (рис. 49). Уравнение лемнискаты имеет вид

.

Составим уравнение лемнискаты еще в полярной системе координат, при­нимая точку О за полюс, а положительную полуось Ох за полярную ось.

Заменяя в уравнении лемнискаты х и у их выражениями через полярные коор­динаты получим или .

При изменении от 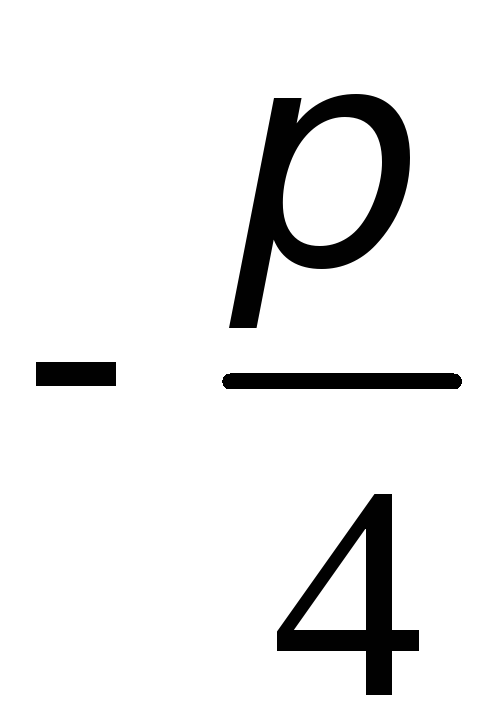до 0 функция возрастает от 0 до , а при изменении от 0 до 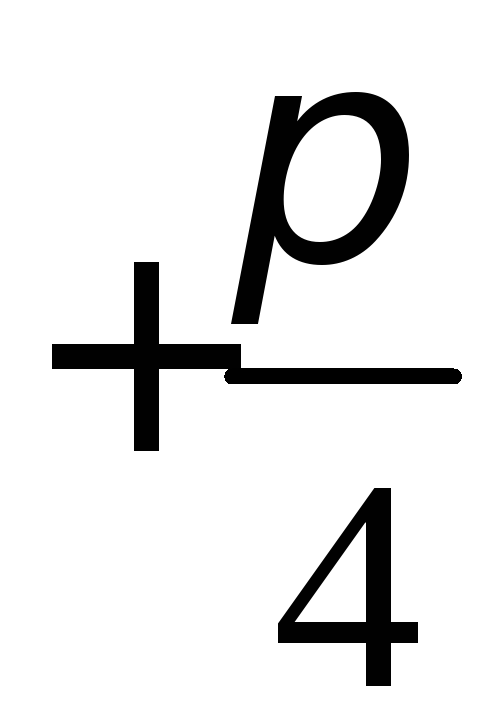- эта функция убывает от до 0; по­лучается петля, расположенная в первой и четвертой четвертях; при изменении отдополучается другая петля, расположенная во второй и третьей четвертях, симметричная пер­вой относительно полюса.

Рис. 49

Значениям , для которыхсоответствуют мнимые значения функции, следовательно, этим значениямне соответствуют никакие точки лемнискаты.

Что касается построения овалов Кассини, то точки этих линий удобнее всего строить, исходя из геометриче­ского определения линии. Уравнения линий иногда удобно со­ставлять в полярной системе координат. Рассмотрим следующий пример линии . Подумайте, что это за линия.