§ 131. Асимптотический конус гиперболоидов.
Два гиперболоида
(один однополостный, другой двуполостный):
 (9)
(9)
называются
сопряжёнными.
Конус второго
порядка, выражаемый уравнением:
 (10)
(10)
называется
асимптотическим конусом для обоих
гиперболоидов.
Докажем, что любая
плоскость, проходящая через ось
 ,
пересекает поверхности (9) по сопряжённым
гиперболам, а асимптотический конус
(10) по двум прямым, которые для этих
сопряженных гипербол являются асимптотами.
В самом деле, повернём оси координат
вокруг оси
,
пересекает поверхности (9) по сопряжённым
гиперболам, а асимптотический конус
(10) по двум прямым, которые для этих
сопряженных гипербол являются асимптотами.
В самом деле, повернём оси координат
вокруг оси на угол
на угол .
.
Уравнения (9) и
(10) в новой системе координат
 будут иметь вид:
будут иметь вид:
 ,
(
,
( )
)
 .
(
.
( )
)
Сечения этих
поверхностей плоскостью
 выражаются уравнениями:
выражаются уравнениями:
 ,
,
 (
( )
)
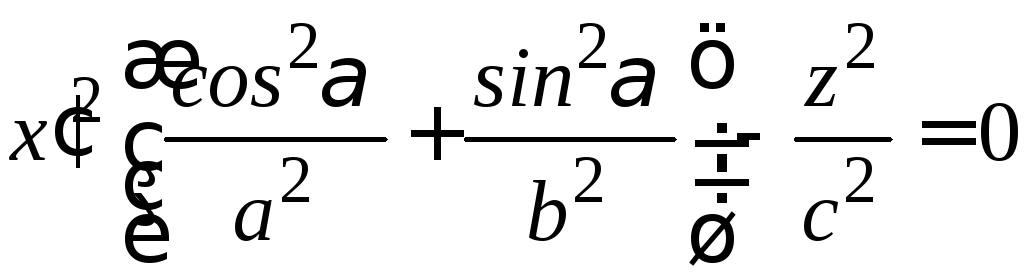 ,
,
 (
( )
)
Из этих уравнений
видно, что сечениями являются две
гиперболы ( )
с полуосями:
)
с полуосями: ,
, ,
а прямые (
,
а прямые ( )
- асимптотами этих гипербол (См. рис.
205).
)
- асимптотами этих гипербол (См. рис.
205).
Заметим, что все
гиперболоиды семейства:
 имеют общий асимптотический конус:
имеют общий асимптотический конус: (См. рис. 206).
(См. рис. 206).
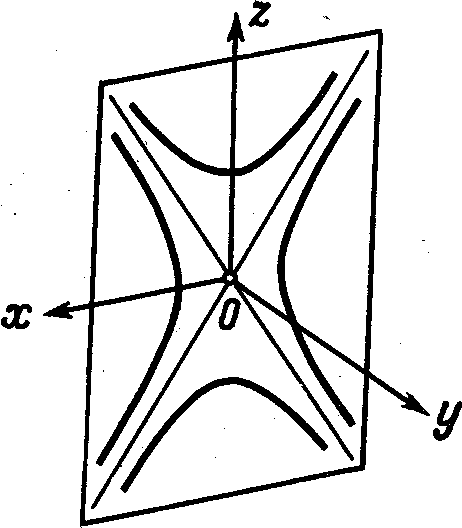
Рис. 205.
Рис. 206.

27


 (9)
(9) (10)
(10) ,
(
,
( .
(
.
( ,
,
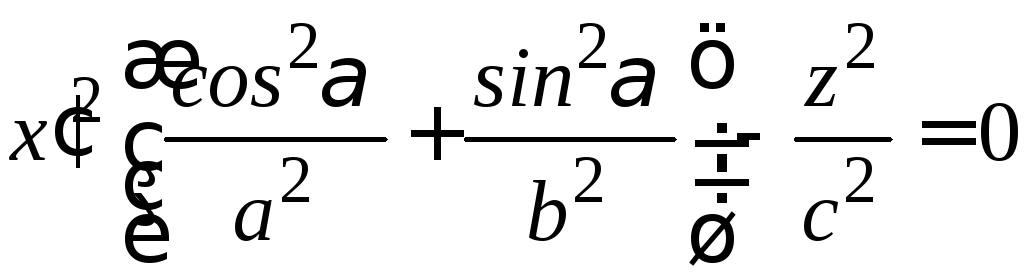 ,
,
 ,
, имеют общий асимптотический конус:
имеют общий асимптотический конус: (См. рис. 206).
(См. рис. 206).
