Кулісні механізми застосовують в строгальних верстатах, поршневих насосах і приладах.

Кулісою звичайно називають ланку з пазом, по якому переміщається повзун (кулісний камінь). Куліса може бути гойдаючуюся, що обертається, рухається поступально.

На рис. 12 наведена схема гидроприводу, в якому циліндр з поршнем замінює кулісний камінь.

Рис. 12

Зубчасті механізми часто використовуються у механізмах і призначені для здійснення потрібного обертального руху.

Найчастіше потрібний рух дістають внаслідок перетворення обертального руху з якоюсь кутовою швидкістю в обертальний рух з іншою кутовою швидкістю.

Механізми, що обслуговують обертальний рух, називають передачами. Тому зубчасті механізми, поряд с пасовими, фрикційними, ланцюговими та іншими належать до передач.

Досить поширені не лише плоскі, а й просторові зубчасті механізми. Ось ведучого і веденого валів зубчастих механізмів можуть бути паралельними, пересічними і перехресними у просторі.

Два циліндричних зубчастих колеса, що передають рух з одного вала на паралельний йому інший вал, можуть утворювати зовнішнє і внутрішнє зачеплення.

На рис. 13. показано зубчасту передачу із зовнішнім зачепленням; вона складається з коліс 1 і 2 та стояка 3.

Рис.13

Поряд із зубчастими механізмами, колеса яких обертаються навколо нерухомих осей, широко застосовують також механізми з валами, підшипники яких встановлено на рухомій рамі (водилі). При цьому зубчасті колеса беруть участь у складному русі, обертаючись не тільки відносно водила, а й разом с ним.

Такі механізми, залежно від числа ведучих ланок називають диференціальними або планетарними. Характерною особливістю диференціальних механізмів є наявність двох чи більше ведучих ланок, а планетарних  однієї ведучої ланки і нерухомого зубчастого колеса, яке називають сонячним. За допомогою диференціальних механізмів (диференціалів) можна здійснювати алгебраїчне додавання кутових швидкостей, а тому їх можна використовувати у верстатах, автомобілях і т.п.

До зубчастих механізмів належать також зірчасті, або цівкові, мальтійські хрести, храпові.

Кулачкові механізми використовують у багатьох машинах і приладах, особливо ву машинах-автоматах, двигунах внутрішнього згоряння, парових машинах і турбiнах, текстильних і поліграфічних машинах.

Рис.14

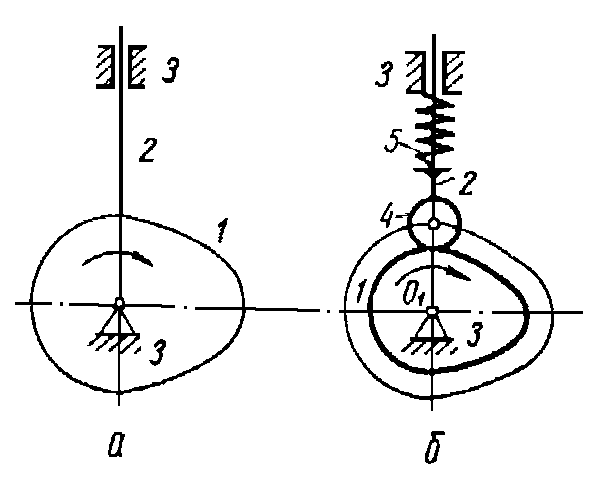
Розглянемо механiзм, що складається з кулачка 1, штовхача 2 і стояка 3 (рис.14, а). Щоб запобігти швидкому спрацюванню бічної поверхні кулачка, на кінці штовхача встановлюють ролік 4 (рис.14, б), який з’єднується з штовхачем на шарнірі, а для замикання елементів вищої кінематичної пари встановлюють пружину 5, яку не0вважають за ланку механізму і не враховують при підрахунку числа ступенів вільності.

На рис.15показано схеми найчастiше застосовуваних кулачкових механізмiв. Один з таких механізмiв, зображений нарис.15, є просторовим, решта - плоскі. Тут позначено ведучу ланку 1, ведену (штовхач) 2 і стояк 3.

Ступінь вільності розглядуваних кулачкових механізмiв можна визначити за відповідною структурною формулою. Найчастіше ступінь рухомостi кулачкових механізмів визначають за структурною формулою Чебишева; звичайно він дорiвнює одиницi. Тому при заданому русі ведучої ланки (кулачка) рух решти рухомих ланок буде цілком визначений.

Частіше застосовують кулачковi механізми з обертовим кулачком (рис. 15, а, д), рідше - з кулачком, що рухається поступально (рис.15, б).

Ведена ланка кулачкового механізму може здійснювати поступальний рух (рис.15, а, б, в) або обертальний - (рис.15, д); дуже рідко - складний плоский.

Рис.15

За типом штовхача кулачкові механізми поділяють на механізми з гострокінцевим штовхачем (рис. 15, а), штовхачем, що має ролик (рис. 15, б, в), плоским (мал. 15, д) штовхачем. Найпоширеніші роликовi штовхачі, бо при цьому тертя ковзання між профiлем кулачка і штовхачем замінюється на тертя кочення, внаслідок чого знижуються втрати на тертя в кінематичних парах механізму і зменшується спрацювання профілю кулачка.

Розглянемо найважливіші означення, що зустрічаються під час аналізу і синтезу кулачкових механізмів. Нарис.16 прийнято такі позначення:

_в- фазовий кут віддалення (піднімання);

_в.п- фазовий кут верхньої паузи;

_наб- кут наближення (опускання);

_н.п.- кут нижньої паузи;

R₀- радіус основної шайби теоретичного профілю кулачка;

г₀- радіус основноі шайби справжнього (робочого) профілю кулачка;

 - радіус-вектор теоретичного профілю кулачка;

г_p- радіус ролика;

h - хiд штовхача.

Дійсним (робочим) профілем кулачка називають профіль, з яким стикається ролик.

У розглядуваному випадку за теоретичний профіль узято траєкторію центра ролика у відносному русі штовхача відносно кулачка. Для механiзму із штовхачем, що має ролик, теоретичний профіль є еквідистантний (рiвновiддалений по нормалi) відносно дійсного.

Радіус-вектор теоретичного профілю завжди дорівнює за модулем відстані вiд осі обертання до вiдповідної радiус-вектору точки теоретичного профілю.

Інтервалам часу віддалення і наближення веденої ланки відповідають ті ділянки теоретичного профілю, на яких радіус-вектор дістає додатний або від'ємний приріст. Інтервалам верхньої і нижньої пауз відповідають ділянки профілю, на яких радіус-вектори сталі величини.

Фазові кути віддалення, верхньої паузи, наближення (повернення) і нижньої

паузи пропорціональнi вiдповідним інтервалам часу.

Тривалість різних циклів руху веденої ланки в часi або за кутом повороту кулачка можна показати на схемі (циклограмі). На поданій нижче циклограмі кожний з чотирьох фазових кутів (кутiв повороту кулачка, що відповідають певним циклам роботи механізму) дорівнює 90.

Рис.16

Сума фазових кутів дорівнює 360:

_в+_в.п.+_наб+_н.п.= 360. (87)

Відповідні інтервали часу пропорціональні фазовим кутам:

t_в+ t_в.п.+ t_наб+ t_н.п.= T, (88)

090180270360

Ланка	Фазовий кут
Кулачок	в.	в.п.	наб	н.п.
Штовхач	Віддалення	Верхня пауза	Наближення	Нижня пауза

де t_в.- час що відповідає віддаленню штовхача;

t_в.п.- тривалість верхньої паузи;

t_наб- час наближення;

t_н.п.- тривалість нижньої паузи;

T - період руху механізму.