1. Лекция: Графы и способы их представления

Приводятся начальные сведения о графах и основные понятия и определения такие как орграф, смешанный граф, дубликат графа дуга, петля, полустепени исхода и захода. Даются возможные способы представления графов. Цель лекции: Дать представление о графах и возможных способах их представления.

Введение

В последние годы особую важность приобрели те разделы математики, которые имеют отношение к развитию цифровых устройств, цифровой связи и цифровых вычислительных машин. Базой для преподавания этих дисциплин наряду с классическими методами анализа непрерывных физических моделей стали алгебраические, логические и комбинаторные методы исследования различных моделей дискретной математики.

Значительно возросла популярность теории графов– ветви дискретной математики.Графывстречаются во многих областях под разными названиями: "структуры" в гражданском строительстве, "сети" – в электронике, "социограммы" – в социологии и экономике, "молекулярные структуры" – в химии, "дорожные карты", электрические или газовые распределительные сети и т. д.

Родившись при решении головоломок и игр, таких, например, как задача о кенигсбергских мостах и игра Гамильтона, теория графовстала мощным средством исследования и решения многих задач, возникающих при изучении больших и сложных систем. Для специалистов по вычислительной технике, информационным системам и системам цифровой связитеория графов– это удобный язык выражения понятий из этой области; многие результаты теории графов имеют непосредственную связь с задачами, с которыми им приходится сталкиваться. Графическая интерпретация различных моделей графов дана на рис. 1.1.

Так в виде ориентированных графов можно представить любую логическую или функционально - логическую схему (рис. 1.1,а). На таких графовых моделях можно, например, оценить быстродействие схемы. Блок-схема алгоритма может быть представлена вероятностным графом (рис. 1.1,б), который позволяет оценить временные характеристики алгоритма, затраты процессорного времени, трудоемкость и другие. Графом типа "дерево" можно отобразить практически любую структуру организации или предприятия (рис. 1.1,в).

Широкое применение теория графовполучила при исследовании так называемой проблемы оптимизации, возникающей при конструировании больших систем как технических, так и программных, например, таких, как компиляторы.

В рамках этих исследований были разработаны многие, неизвестные ранее теоретико-графовые понятия. Теория графовимеет большую привлекательность для специалистов в области проектирования для построения эффективных алгоритмов и анализа их сложности. Использование аппарата теории графов оказало существенное влияние на разработку алгоритмов конструкторского проектирования схем. Непосредственное и детальное представление практических систем, таких, как распределительные сети, системы связи, приводит к графам большого размера, успешный анализ которых зависит в равной степени, как от эффективных алгоритмов, так и от возможностей компьютерной техники. Поэтому в настоящее время основное внимание сосредоточено на разработке и описании компьютерных алгоритмов анализа графов. В связи с этим основной упор в данном учебном пособии делается на машинные способы представления графов и алгоритмы решения задач на графах, легко реализуемых на ЭВМ.

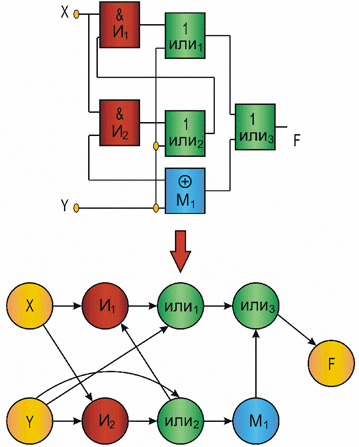
a

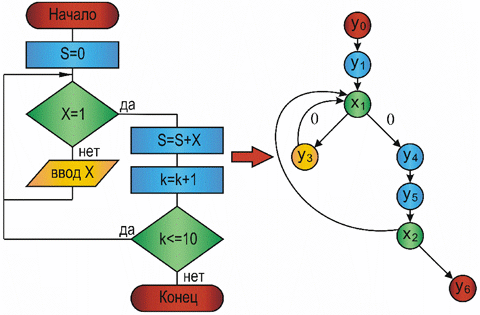
б

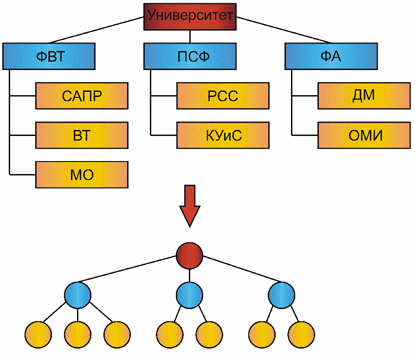
в

Рис. 1.1. Графическая интерпретация применения графовых структур: а – орграф; б – вероятностный граф; в – граф-дерево

Графы и способы их представления

Основные определения

Граф задается множеством точек или вершинх₁, х₂, ..., х_nи множеством линий или реберa₁, a₂, ... , a_m, соединяющих между собой все или часть точек. Формальное определение графа может быть дано следующим образом.

Графомназывается двойка вида

G = (X, A),

где X = {x_i}, i = 1, 2, ..., n– множество вершин графа,A = {a_i}, i = 1, 2,... , m– множество ребер графа.

Графымогут быть ориентированными, неориентированными и смешанными (рис. 1.2). Если ребра у множестваAориентированы, что обычно показывается стрелкой, то они называются дугами, играфс такими ребрами называется ориентированнымграфомилиорграфом(рис. 1.2,а).

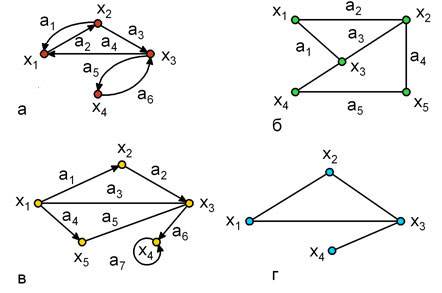
Рис. 1.2.

Если ребра не имеют ориентации, то графназывается неориентированным (рис. 1.2,б).Граф, в котором присутствуют и ребра, и дуги называется смешанным (рис. 1.2,в). В случае, когдаG = (X, A)являетсяорграфом, и мы хотим пренебречь направленностью дуг из множестваA, то неориентированный граф, соответствующийG, будет обозначаться и называться неориентированным дубликатом или неориентированным двойником (рис. 1.2,г).

Дуга a_i может быть представлена упорядоченной парой вершин(х_n, х_k), состоящей из начальнойх_nи конечнойх_kвершин. Например, дляграфаG₁(рис. 1.2,а) дугаa₁ задается парой вершин(x₂, x₁), а дугаа₃парой(x₂, x₃). Еслих_n,х_k– концевые вершины дугиa_i, то говорят, что вершиных_nих_kинцидентны дугеa_iили дугаa_i инцидентна вершинамх_nих_k.

Дуга, у которой начальная и конечная вершины совпадают, называется петлей. В графе G₃ (рис. 1.2,в) дугаa₇ является петлей.

Каждая вершина орграфах_i может характеризоватьсяполустепенью исходаd₀(х_i)иполустепенью заходаd_t(х_i).

Полустепенью исходавершиных_i—d₀(х_i)называется количество дуг, исходящих из этой вершины. Например, дляорграфаG₁(рис. 1.2,а) характеристики полустепеней исхода следующие:d₀(х₁)=1,d₀(х₂)=2,d₀(х₃)=2,d₀(х₄ )=1.

Полустепенью заходавершиных_i—d_t(х_i)называется количество дуг, входящих в эту вершину. Например, дляорграфаG₁:d_t(х₁)=2,d_t(х₂)=1,d_t(х₃)=2,d_t(х₄ )=1.

Очевидно, что сумма полустепеней исхода всех вершин графа, а также сумма полустепеней захода всех вершин графа равна общему числу дуг графа, т. е.

ⁿ_i=1d₀(x_i)= ⁿ_i=1d_t(x_i)=m

где n– число вершин графа,m– число дуг.

Каждая вершина неориентированного графах_i может характеризоваться степенью вершиныd(х_i).

Степенью вершины х_i–d(х_i)называется количество ребер, инцидентных этой вершине. Например, дляорграфаG₁(рис. 1.2,б) характеристики степеней следующие:d(х₁)=2,d(х₂)=3,d(х₃)=3,d(х₄ )=2.

Способы описания графов

Теоретико-множественное представление графов

Графописывается перечислением множества вершин и дуг. Примеры описания приведены дляорграфовна рис. 1.3 и рис. 1.4.

G₄ = (Х, А),

где Х = {х_i},i = 1, 2, 3, 4– множество вершин;А = {a_i },i = 1, 2, ..., 6– множество дуг, причемА = {(х₁, х₂), (х₄, х₂), (х₂, х₄ ), (х₂, х₃), (х₃, х₃), (х₄ , х₁)}.

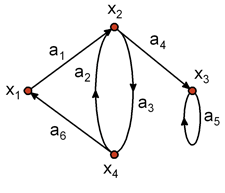
Рис. 1.3.

G₅ = (X, A),

где X = {B, C, D, E, F}– множество вершинграфа,A = {a_i},i = 1, 2, ..., 5– множество дугграфа, причемa₁ = (F, B),a₂ = (B, E),a₃ = (F, D),a₄ = (E, C),a₅ = (C, D).

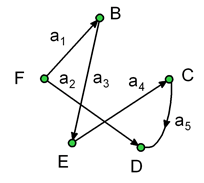
Рис. 1.4.

Задание графов соответствием

Описание графовсостоит в задании множества вершинХи соответствияГ, которое показывает, как между собой связаны вершины.

Соответствием Гназывается отображение множестваХвХ, аграфв этом случае обозначается паройG = (X, Г).

Отображением вершины х_i —Г(х_i)является множество вершин, в которые существуют дуги из вершиных_i, т. е.Г(х_i) = { х_j: дуга (х_i, х_j) A}.

Так для орграфана рис. 1.3 описание заданием множества вершин и соответствия выглядит следующим образом:

G₄=(X, Г),

где X = {х_i},I = 1, 2, ..., 4– множество вершин,Г(х₁) = { х₂ },Г(х₂) = { х₃, х₄ },

Г(х₃) = { х₃ },Г(х₄) = { х₁, х₂ }– отображения.

Для неориентированного или смешанного графовпредполагается, что соответствиеГ задает такой эквивалентный ориентированныйграф, который получается из исходногографазаменой каждого неориентированного ребра двумя противоположно направленными дугами, соединяющими те же самые вершины. Например, дляграфана рис. 1.2,бГ(х₂) = { х₁, х₃, х₅ },Г(х₄) ={ х₃, х₅}и т. д.

Матричное представление графов

Для обработки на ЭВМ графыудобно представлять в видематриц смежностииинциденций.

Матрица смежности– это квадратная матрица размерностьюn xn, (гдеn– число вершинграфа), однозначно представляющая его структуру.

A = {a_ij},i, j = 1, 2, ..., n, а каждый элемент матрицы определяется следующим образом:

a_ij = 1, еслидуга(х_i, х_j),

a_ij = 0, если нет дуги(х_i, х_j).

Матрица инциденцийпредставляет собой прямоугольную матрицу размеромn x m, гдеn– количество вершинграфа, аm– количество дугграфа. Обозначается матрица инциденцийB = {b_ij},i = 1, 2, ..., n,j = 1, 2, ..., m.

Каждый элемент матрицы определяется следующим образом:

b_ij = 1, еслих_i является начальной вершиной дугиa_j,

b_ij = –1, еслих_iявляется конечной вершиной дугиa_j,

b_ij = 0, еслих_iне является концевой вершиной дугиa_jили еслиa_jявляется петлей.

На рис. 1.5, а,б приведен графи егоматрица смежности, по которой можно найти характеристики вершин. Так сумма элементовi-ой строки матрицы даетполустепень исхода вершиных_i, а сумма элементовi-го столбца даетполустепень заходавершиных_i. Поматрице смежностиможно найти прямые и обратные отображения. Рассмотримi-ю строку матрицы. Если элементa_ij=1, то элементграфах_jвходит в отображениеГ(х_i). Например, во 2-й строке матрицыА(рис. 1.5,б) единицы стоят в 2-м и 5-м столбцах, следовательно,Г(х₂) = { х₂, х₅}.

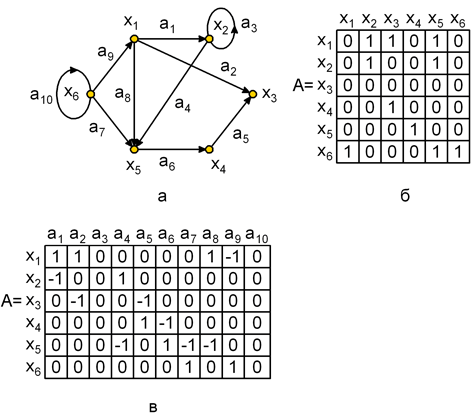
Рис. 1.5. Орграфи его матричное представление: а –орграф; б – матрица смежности; в – матрица инциденций

Для графана рис. 1.5,аматрица инциденцийприведена на рис. 1.5,в. Поскольку каждая дуга инцидентна двум различным вершинам, за исключением того случая, когда дуга образует петлю, то каждый столбец либо содержит один элемент равный 1 и один – равный – 1, либо все элементы столбца равны 0.

Для неориентированного графа,матрица инциденцийопределяется так же, за исключением того, что все элементы, равные –1, заменяются на 1.

2. Лекция: Операции над графами

Приводятся основные операции над графами такие как объединение, пересечение, кольцевая сумма, удаление вершины, удаление ребра, замыкание и стягивание. Эти операции рассматриваются для представления графов матрицами смежности. Цель лекции: Дать представление об операциях над графами и возможных способах их представления в матричных структурах.

Рассмотрим семь операций над графами, три из которых являются бинарными, включающими два графа, а остальные четыре – унарные, т. е. определены на одномграфе.

Объединение графовG₁ иG₂, обозначаемое какG₁ G₂, представляет такой графG₃ = (Х₁ Х₂, A₁ A₂), что множество его вершин является объединениемХ₁иХ₂, а множество ребер – объединениемA₁иA₂. ГрафG₃, полученный операцией объединения графовG₁иG₂, показан на рис. 2.1,д, а его матрица смежности – на рис. 2.1,е. Матрица смежности результирующего графа получается операцией поэлементного логического сложения матриц смежности исходных графовG₁иG₂.

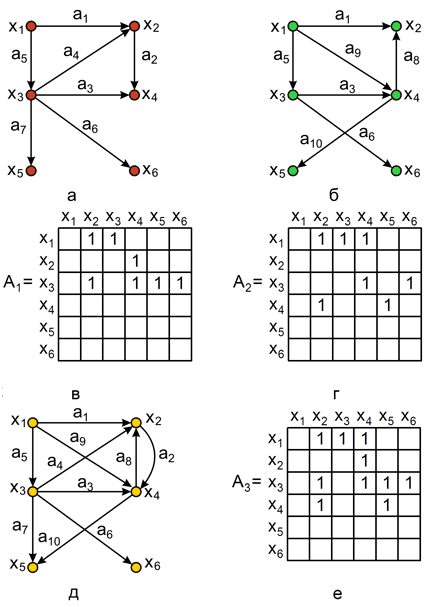
Рис. 2.1.

Пересечение графовG₁иG₂, обозначаемое какG₁ G₂, представляет собойграфG₄ = (Х₁ Х₂, A₁ A₂). Таким образом, множество вершинграфаG₄состоит из вершин, присутствующих одновременно вG₁иG₂. Операция пересеченияграфов G₁ G₂показана на рис. 2.2,в, а результирующая матрица смежности получается операцией поэлементного логического умножения матриц смежности исходныхграфовG₁иG₂. показана на рис. 2.2.г.

Рис.2.2. Операция пересечения и кольцевой суммы: а – граф G₁; б – графG₂;

в – граф G₁ G₂; г – матрица смежности графаG₁ G₂; д – графG₁ G₂; е – матрица смежности графаG₁ G₂

Кольцевая суммадвухграфовG₁иG₂, обозначаемая какG₁ G₂, представляет собойграфG₅, порожденный на множестве реберA₁ A₂. Другими словами,графG₅не имеет изолированных вершин и состоит только из ребер, присутствующих либо вG₁ , либо вG₂, но не в обоих одновременно. Кольцевая суммаграфовG₁иG₂ показана на рис. 2.2,д, а результирующая матрица смежности получается операцией поэлементного логического сложения поmod 2матриц смежности исходных графовG₁иG₂. показана на рис. 2.2.е.

Легко убедиться в том, что три рассмотренные операции коммутативны

т. е. G₁ G₂ = G₂ G₁, G₁ G₂ = G₂ G₁, G₁ G₂ = G₂ G₁ ,

и многоместны,

т. е. G₁ G₂ G₃ G₄ ...,G₁G₂ G₃G₄ ...и так далее.

Рассмотрим унарные операции на графе.

Удаление вершины. Еслих_i-вершина графаG = (X, A), тоG–х_i-порожденный подграфграфаGна множестве вершинX–х_i, т. е.G–х_iявляетсяграфом, получившимся после удаления изграфаG вершиных_i и всех ребер, инцидентных этой вершине. Удаление вершиных₃ показано на рис. 2.3,б (для исходного графа, изображенного на рис. 2.3,а). Матрица смежности исходногографа представлена на таблице 2.1а). Результирующая матрица смежностиграфа после выполнения операции удаления вершиных_iполучается путем удаления соответствующегоi- го столбца иi-ой строки из исходной матрицы и "сжимания" матрицы по вертикали и горизонтали начиная с(i+1)- го столбца и(i+1)-ой строки (таблица 2.1б). В дальнейшем элементы графа могут быть переобозначены.

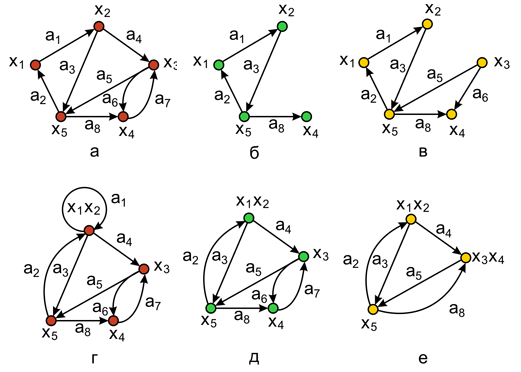
Рис. 2.3.

Удаление ребраилиудаление дуги. Еслиa_i -дугаграфаG = (X, A),тоG-a_i – подграфграфаG, получающийся после удаления изGдугиa_i. Заметим, что концевые вершины дугиa_i не удаляются. Удаление изграфамножества вершин или дуг определяется как последовательное удаление определенных вершин или дуг. Удаление дугa₄ иa₇показано на рис. 2.3,в. Результирующая матрица смежностиграфапосле выполнения операции удаления дуги ai получается путем удаления соответствующих элементов из исходной матрицы (таблица 2.1в).

Замыкание или отождествление. Говорят, что пара вершинх_i иx_jвграфеGзамыкается (или отождествляется), если они заменяются такой новой вершиной, что все дуги вграфеG, инцидентныех_iиx_j, становятся инцидентными новой вершине. Например, результат замыкания вершиных₁ их₂показан на рис. 2.3,г дляграфаG(рис. 2.3,а). Матрица смежностиграфапосле выполнения операции замыкания вершинх_iиx_j получается путем поэлементного логического сложенияi- го иj- го столбцов иi-ой иj- строк в исходной матрице и "сжимания" матрицы по вертикали и горизонтали (таблица 2.1г).

Стягивание. Под стягиванием подразумевают операцию удаления дуги или ребра и отождествление его концевых вершин.Граф, изображенный на рис. 2.3,д получен стягиванием дугиa₁, а на рис. 2.3,е – стягиванием дугa₁ ,a₆ иa₇. Соответствующие результирующие матрицы смежности показаны в таблицах 2.1д и 2.1е.

3.Лекция: Многозначные отображения и транзитивные замыкания

Рассматриваются прямые и обратные отображения для орграфов различных порядков. Даются понятия прямого и обратного транзитивного замыкания и способы нахождения транзитивных замыканий по матрице смежности. Цель лекции: Дать представление о многозначных отображениях и транзитивных замыканиях и способах их нахождения.

Многозначные отображения

Прямые отображения

Прямым отображением 1-го порядка вершины х_i является множество таких вершинграфа, для которых существует дуга(х_i, x_j), т. еГ¹( х_i ) = {x_j : дуга (х_i, x_j) A}дляграфа

G = (X, A), гдеX ={ х_i },i =1, 2, ..., n– множество вершин, аA = {a_i},i = 1, 2, ..., m– множество дуг.

Прямое отображение 2-го порядка вершины х_i – это прямое отображение от прямого отображения 1-го порядка, т. е.Г⁺²( х_i ) = Г⁺( Г⁺¹ ( х_i ) ).

Аналогично можно записать для прямого отображения 3-го и т. д. n-го порядка.

Г⁺³(x_i)= Г⁺(Г⁺²(x_i))= Г⁺(Г⁺(Г⁺¹(x_i)))

...

Г⁺ⁿ(x_i)=Г⁺(Г^+(n-1)(x_i)).

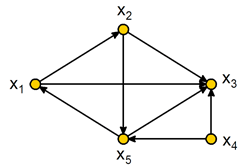
Рис. 3.1. Орграф G

Прямые многозначные отображения для графа на рис. 3.1 находятся следующим образом:

Г⁺¹(x₁)=(x₂,x₃),

Г⁺²(x₁)=Г⁺(Г⁺¹(x₁))=Г⁺(x₂,x₃)=(x₃,x₅),

Г⁺³(x₁)=Г⁺(Г⁺²(x₁))=Г⁺(x₃,x₅)=(x₃,x₁)и т. д.

Обратные отображения

Обратным отображением 1-го порядка для вершины х_iявляется множество элементовx_j таких, что существует дуга(x_j, х_i), принадлежащая множеству дуг графа, т. е.

Г^-1(х_i ) = { x_j : дуга (х_j, х_i) А }.

Обратные отображения 2-го, 3-го и т. д. n-го порядка определяются следующим образом:

Г^-2(x_i)= Г^-(Г^-1(x_i)),

Г^-3(x_i)= Г^-(Г^-2(x_i)),

...

Г^-n(x_i)= Г^-(Г^-(n-1)(x_i)).

Для графа на рис. 3.1 обратные многозначные отображения вершины х₁ находятся следующим образом:

Г^-1(x₁)=x₅,

Г^-2(x₁)= Г^-(Г^-1(x₁))=Г^-(x₅)= x₂,x₄,

Г^-3(x₁)= Г^-(Г^-2(x₁))=Г^-(x₂x₄)= x₁,

Г^-4(x₁)= Г^-(Г^-3(x₁))=Г^-(x₁)= x₅и т.д.

П р и м е ч а н и я:

1. Когда отображение действует не на одну вершину, а на множество вершин

Х_q = { х₁, х₂, ..., х_q }, то подГ(Х_q)понимают объединение

Г(х₁) Г(х₂) ...Г(х_q).

2. Многозначное отображениедля неориентированногографастроится, если представить каждое ребро двумя противоположно направленными дугами (рис. 3.2).

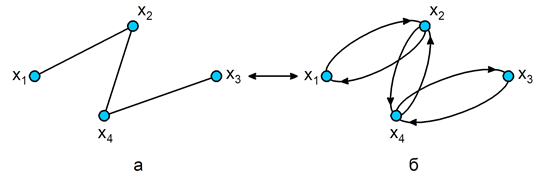
Рис. 3.2. Граф: а – неориентированный; б – тождественный ему ориентированный

http://images.google.com/imgres?imgurl=http://www.intuit.ru/department/algorithms/ingrth/5/05-04.gif&imgrefurl=http://www.intuit.ru/department/algorithms/ingrth/5/&usg=__KPXfdLHNyY_u3OpFt0mrYtULRVQ=&h=358&w=315&sz=9&hl=ru&start=3&um=1&tbnid=vTFUql_rFlKhIM:&tbnh=121&tbnw=106&prev=/images%3Fq%3D%25D0%25B3%25D1%2580%25D0%25B0%25D1%2584%25D1%258B%26hl%3Dru%26client%3Dopera%26rls%3Dru%26sa%3DX%26um%3D1

Транзитивные замыкания

Прямое транзитивное замыкание

Прямым транзитивным замыканиемнекоторой вершиных_i – T⁺( х_i )является объединение самой вершиных_iс прямыми отображениями 1-го порядка, второго порядка и т. д., т. е.

T⁺( х_i ) = х_i Г⁺¹ ( х_i ) Г⁺²( х_i ) ...

Многозначные отображения находятся до тех пор, пока в них добавляются новые вершины.

Так, для графа на рис. 3.1.

Г⁺¹ ( х₁ ) = { х₂, х₃ }, Г⁺²( х₁ ) = { х₃, х₅ }, Г⁺³( х₁ ) = { х3, х₁ }, Г⁺⁴( х₁ ) = { х₂, х₃ }.

Отображение четвертого порядка содержит те же элементы, что и отображение 1-го порядка, следовательно, других элементов в последующих отображениях не появится. Транзитивное замыканиедля вершиных₁получается следующим образом:

T⁺( х₁ ) = х₁ { х₂, х₃ } { х₃, х₅ } { х₃, х₁ } = { х₁, х₂, х₃, х₅ }.

Проанализировав множество вершин, входящих в T⁺( х_i ), можно сделать вывод:прямое транзитивное замыканиесодержит вершины, в которые есть пути из вершиных_i. Таким образом, можно дать второе определениеT⁺( х_i ).

Прямое транзитивное замыканиенекоторой вершиных_iT⁺( х_i ) – это множество вершин, достижимых из вершиных_i, т. е.T ( х_i ) = { х_j | путь из х_i в х_j }.

Обратное транзитивное замыкание

Обратным транзитивным замыканиемнекоторой вершиных_i –T^-( х_i )является объединение этой вершины с обратными отображениями 1-го, 2-го и т. д.n-го порядка, т. е.

T^-( х_i ) = х_i Г^-1(х_i ) Г^-2(х_i ) ...

Иначе, обратное транзитивное замыкание для некоторой вершины х_i –T^-( х_i )– это множество вершин, из которых достижима вершина х_i,

т. е. T^-( х_i ) = { xj | путь из x_j в х_i }.

Рассмотрим построение обратного транзитивного замыкания для графа на рис. 3.1.

Г^-1(х₁) = { х₅ }, Г^-2(х₁) = { х₂, х₄ }, Г^-3(х₁) = { х₁ }, Г^-4 (х₁) = { х₅ },

T^-(х₁) = х₁ { х₅ }{ х₂, х₄ } { х₁ } { х₅ } = {х₁, х₂, х₄, х₅}.

Нахождение транзитивных замыканий по матрице смежности

Рассмотрим метод нахождения прямого транзитивного замыкания по матрице смежности, показанной на рис. 3.3,а для вершины х₂графа, изображенного на рис. 3.3,б. На 1-м шаге итерации заносим 0 в столбецТ⁺для элементах₂и просматриваем 2-ю строку матрицы. Находим, что элементыa₂₂=1 иa₂₅=1. Заносим 1 в 5-ю клеткуТ⁺. 2-я клетка уже занята нулем, поэтому 1 не заносим. 2-й шаг начинается просмотром 5-й строки матрицы смежности, соответствующий вершинех₅графа. Находим, что элементыa₅₁=1иa₅₄=1, т. е. из вершиных₅имеются дуги в вершиных₁их₄или иначе из вершиных₂имеются пути длиной 2 в вершиных₁их₄. Длину пути 2 заносим в 1-ю и 4-ю клетки столбцаT⁺(х₂). На 3-м шаге анализируются 1-я и 4-я строки матрицы смежностиА. Находим элементыa₁₂=1,a₁₃=1,a₄₃=1. В соответствующие свободные клетки

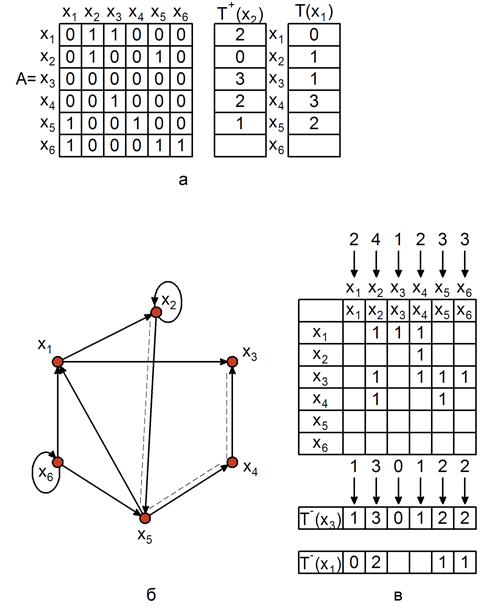
Рис. 3.3. Построение прямого (а) и обратного (в) транзитивных замыканий для графа(б)

Это возможно сделать только для вершины х₃, так как вторая клетка уже занята. Анализ 3-й строки матрицы на 4-м шаге показывает, что из вершиных₃нет исходящих дуг, следовательно, процесс формированияпрямого транзитивного замыканиязавершен.

Таким образом, в столбце T⁺(х₂)стоят числа равные длине пути от вершиных₂к соответствующим вершинамграфа. Путь отх₂кх₃равный 3 показан штриховой линией на рис. 3.3,б. В столбцеT⁺( х₂ )отмечены все вершины, достижимые из вершиных₂, следовательно, они входят вT⁺( х₂ ).

T⁺( х₂ ) = { х₁, х₂, х₃, х₄, х₅ }.

Во втором столбце показано построение прямого транзитивного замыканиявершиных₁ – T⁺( х₁ ).

T⁺( х₁ ) = { х₁, х₂, х₃, х₄, х₅ }.

Нахождение обратного транзитивного замыканияпо матрице смежности показано на рис. 3.1,в. Рассмотрим нахождениеобратного транзитивного замыканиявершиных₃– T^-( х₃ ), которое начинается с занесения 0 в 3-ю клетку строкиT^-( х₃ ). На 1-м шаге алгоритма, помеченного стрелкой с цифрой 1, просматриваем 3-й столбец матрицыА. Определяем элементы равные 1, т. е.a₁₃=1иa₄₃=1. Следовательно, вграфеиз вершинх₁их₄есть дуги в вершинух₃. Заносим 1 в 1-ю и 4-ю клеткиT^-(х₃). На втором шаге просматриваем 1-й и 4-й столбцы матрицыA. Находимa₅₁=1,a₆₁=1,a₅₄=1и проставляем 2 (так как длина пути от этих вершин до вершиных₃равна 2) в свободные клеткиT^-(х₃), т. е. в 5-ю и 6-ю клетки. 3-й шаг заключается в просмотре 5-го и 6-го столбцов матрицыA. Элементыa₂₅=1,a₆₅=1,a₆₆=1позволяют поставить 3 во 2-ю клетку строкиT^-( х₃ ). 4-й шаг просмотра 2-го столбца дает элементыa₁₂ = 1иa₂₂ = 1, уже вошедшие вT^-(х₃). Итак, сформировано обратное транзитивное замыкание для вершиных₃.

T^-( х₃ ) = { х₁, х₂, х₃, х₄, х₅, х₆ }.

Числа, стоящие в клетках T^-( х₃ ), показывают длину кратчайшего пути от соответствующих вершин до вершиных₃.

Во второй строке показано формирование обратного транзитивного замыкания вершины х₁.

T^-( х₁ ) = { х₁, х₂, х₅, х₆ }.