МОТС / МЕТОДИЧЕСКИЕ УКАЗАНИЯ по МОТС №1
.docМЕТОДИЧЕСКИЕ УКАЗАНИЯ
для проведения лабораторной работы по дисциплине
“Математические основы теории систем”
Тема I. Основы теории графов.
Цель работы: Получить практические навыки по отысканию кратчайшего пути в графе с ребрами произвольной длины.
Задание на лабораторную работу:
-
Найти решение задачи о кратчайшем пути в графе с ребрами произвольной длины, соответствующее определенному варианту задания (см. Приложение).
-
Полученные результаты занести в отчет.
-
Сделать вывод по результатам работы.
Теоретические сведения
Граф - это множество точек плоскости, называемых вершинами, и множество направленных отрезков, соединяющих все или некоторые из вершин и называемых дугами.
Способы задания графа:
-
Двумя множествами: множеством вершин X и множеством дуг U
G ={X, U}.
-
Множеством вершин X и отображением F, которое отображает множество X само в себя: G = {X, F}.
Определение 1: Две вершины x и y являются смежными, если они различны и если существует дуга, идущая из x в y .
Определение 2: Дуга u называется инцидентной вершине x, если она заходит в эту вершину или исходит из нее.
Обозначим через x1, x2, … , xn вершины графа, а через u1, u2, … , um - его дуги. Введем числа:
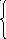
1, если имеется дуга, соединяющая вершину i с вершиной j;
rij =
0, если такой дуги нет.
Матрица R = [rij] называется матрицей смежности графа. Строки и столбцы матрицы смежности соответствуют вершинам графа.
Дуга, инцидентная только одной вершине, называется петлей. Если в главной диагонали есть 1, то в графе есть петли.
Введем далее числа:
+1,
если дуга uij
исходит из
xi;
sij = - 1, если дуга uij заходит в вершину xj;
0, если uij не инцидентна вершине x.
Матрица
S
= [sij]
порядка n
m
называется матрицей
инциденций
для дуг графа.
Путь
- последовательность дуг
,
в которой конец каждой предыдущей
дуги совпадает с началом следующей.
Длиной
пути
называется число l(
),
равное числу дуг, составляющих путь.
Путь может быть конечным и бесконечным.
Контур - это конечный путь, у которого начальная вершина совпадает с конечной. При этом контур называется элементарным, если все его вершины различны, за исключением начальной и конечной.
Контур единичной длины называется петлей.
Граф без учета ориентации называется неориентированным. Дуги называются ребрами. В неориентированном графе вместо понятий путь и контур используют понятия цепь и цикл.
Связный граф - это граф, в котором две любые его вершины можно соединить цепью.
Задача о кратчайшем пути.
Дан
неориентированный граф G
= (X,
U).
Каждому ребру приписано некоторое
число l
(u)
≥ 0, называемое длиной ребра. При этом
любая цепь
будет характеризоваться длиной
.
Требуется
для двух произвольных вершин a
и b
графа G
найти путь
,
причем такой, чтобы его длина была
наименьшей.
Задача распадается на две:
-
Нахождение кратчайшего пути в графе с ребрами единичной длины (или с ребрами равной длины).
-
Нахождение кратчайшего пути в графе с ребрами произвольной длины.
Нахождение кратчайшего пути в графе с ребрами единичной длины (или с ребрами равной длины).
-
Приписываем конечной вершине индекс 0.
-
Помечаем 1 все смежные вершины.
-
Находим все вершины, смежные вершинам, имеющим индекс 1, и приписываем им индекс 2.
-
И т.д., пока не будут помечены все вершины. Значение индекса начальной вершины будет длиной пути.
Нахождение кратчайшего пути в графе с ребрами произвольной длины.
-
Каждая вершина xi помечается индексом
i.
Конечной вершине приписываем
индекс
0
=0. Для
остальных вершин предварительно
полагаем
i
=
(i
).
-
Ищем такую дугу (xi, xj), для которой
i
-
j
> l
(uij),
и заменяем индекс
j
индексом
j’
=
i
+ l
(uij)
<
j.
Продолжаем этот процесс замены
индексов до тех пор, пока остается
хотя бы одна дуга, для которой можно
уменьшить
j.
Если какую–то вершину можно пометить несколькими способами, то выбирается наименьшее значение.
Сформулируем правило для нахождения кратчайшего пути:
Пусть
xn
=a
– начальная вершина с индексом
n.
Ищем вершину xp1,
такую, что
n
-
p1
= l
(un,p1).
Далее ищем вершину xp2,
такую, что
p1
-
p2
= l
(up1,p2)
и т.д. до тех пор, пока не дойдем до
конечной вершины.
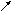
П
2
9
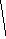
3
2
5
8 3
5 7
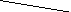5
6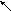
11
*
Найти кратчайший путь из вершины 6 в вершину 1.
-
Вершине 1 присваиваем индекс «0». Для остальных вершин полагаем
i
=
. -
Ищем дугу, для которой
j
-
1>
l(xj,x1).
Это дуги (x1,
x2)
и (x1,
x3). -
Приписываем вершинам 2 и 3 индексы
2’
=
1+
l
(x0,x2)
= 0 + 2 = 2;
3’=
1+
l
(x0,x3)
= 0 + 9 = 9. -
Далее ищем дуги, для которых
j
-
2
> l
(xj,
x2);
j
-
3
> l
(xj,
x3). -
Вершинам 4, 5 приписываем индекс
4’
=
2
+ l
(x2,
x4)
= 2 + 3 = 5,
5’=
2
+ l
(x2,
x5)
= 2 + 3 = 5. Вершине 6 приписываем индекс
6’=
3
+ l
(x3,x6)
=
9
+
7
=
16.
-
Вершину 6 можно пометить из вершины 4, так как
6
-
4
> l
(x4,
x6);
16–5
> 6 ;
6’
=
4
+ l
(x4,
x6)
= 5 + 6 = 11.
Находим
кратчайший путь. Индекс вершины 6
равен 11, значит, длина кратчайшего
пути равна 11. Ищем вершину, для которой
6
-
j
= l
(x6,
xj).
Это вершина 4: 11 – 6 = 5. Значит, первой
промежуточной вершиной на пути 6 –
1 является вершина 4. Далее ищем
вершину, для которой
4
-
j
= l
(x4,
xj).
Это вершина 2: 5 – 2 = 3. И так далее,
пока не дойдем до вершины 1.
Получаем кратчайший путь из вершины 6 в вершину 1: 6 – 4 – 2 – 1, длина которого равна индексу вершины 6, т.е. равна 11.
Приложение.
8
2 3 4 5 5 5 7 7 6 6 8 10 3 2 2 7 4 4 5 5 8 8 10 10 10 2 2 2 6 6 4 5 4 5 3 3 3 10
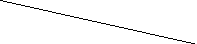
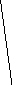
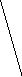
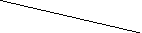
3 4 7 5 4 6 8 8 10 10 10 2 6 7 10 7 3 5 2 6 4 7 10 5 4 6 8 10 8 2 7 6 3 4 5 12 8
3 4 4 3 2 5 5 7 7 8 8 10
