§ 2. Предел функции.

Определение 1. ПустьАВ.Точках₀Вназываетсяточкой сгущения множестваА, если в любой ее окрестности найдется точкахА,хх₀.

Вставка 1.

Определение 2 (по Гейне). Пустьх₀R{} – точка сгущения множестваD_f. ЧислоаR{}называется пределом функцииfв точкех₀(или прих х₀), если{x_n} (x_nD_f,x_nх₀ n N), сходящейся кх₀(), соответствующая последовательность {f(x_n)} значений функцииf сходится к числуа().

В этом случае пишут илиf(x)a прих х₀.

Вставка 2.

Определение3 (по Гейне). Пустьх₀R{} – точка сгущения множестваD_f. ЧислоаR{} называетсяпределомфункцииf в точкех₀справа(слева), если{x_n}D_f,x_n>x₀(x_n<x₀), сходящейся кх₀, соответствующая последовательность {f(x_n)} сходится к числуа.

В этом случае будем писать .

Правосторонний и левосторонний пределы называются еще одностороннимии обозначаются соответственноf(x₀+),f(x₀-).

Вставка 3.

Определение4 (по Коши, на языке окрестностей). Пустьх₀R{} – точка сгущения множестваD_f.Числоа R{} называется пределом функцииfв точкех₀, если> 0=() > 0:.

Расшифровывая понятие окрестности в конкретных случаях, получим различные определения, например.

Определение5 (по Коши,на языке « - » ). Пустьх₀R– точка сгущения множестваD_f. Числоа Rназывается пределом функцииf в точкех₀, если> 0=() > 0:xD_f, 0 < |x –x₀| <,|f(x) –a| <.

Вставка 4.

Определение 6., если₀> 0:  > 0 x  .

Вставка 5.

Определение 7 (по Коши,на языке « - » ). Пустьх₀,аRи х₀- точка сгущения множестваD_f. , если> 0=() > 0:xD_f,x₀<x <x₀ + (x₀ - <x<x₀)|f(x) –a| <.

Аналогично можно сформулировать понятия: .

Вставка 6.

Теорема. Определения пределов функции в точке по Гейне и по Коши эквивалентны.

Доказательство. Рассмотрим случай х₀,аR.

1) Пусть по Коши. Выберем произвольную последовательность,. Это можно сделать, посколькух₀– точка сгущения множестваD_f.

Пусть > 0 и=() > 0 выбраны согласно определению 5. Так как, тоn₀:n>n₀0 < |x_n–x₀| < . Поэтому в силу неравенства |f(x) –a| < для 0 < |x–x₀| <будет выполнено неравенство |f(x_n) –a| < . А так как последовательность {x_n} – произвольная, то а является пределом функцииf в точкех₀ по Гейне.

2) Пусть теперь число аявляется пределом функцииf в точкех₀ по Гейне. Предположим, чтоане является пределом функцииfв точкех₀ по Коши. Тогда, согласно определению 6, для некоторого₀> 0 и> 0x .

Если, например, выберем последовательность , то_n x_nD_f: и . Первое неравенство означает, что,х_nx₀. Но тогда, т.к.а есть предел функцииf в точкех₀ по Гейне должны получить, что противоречит второму неравенству. Значит, наше предположение о том, чтоа не является пределом функцииf в точкех₀ по Коши, не верно.

Вопросы и упражнения.

1. Принадлежит ли точка сгущения некоторого множества самому множеству?

2. Имеют ли конечные множества точки сгущения?

3. Сравнить понятия «точка сгущения множества» и «предельная точка».

4. Доказать единственность предела функции в точке.

5. Доказать: 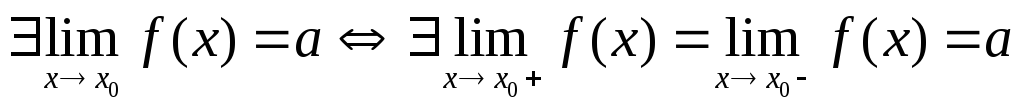,аR.

6. Сформулировать определение по Гейне: .

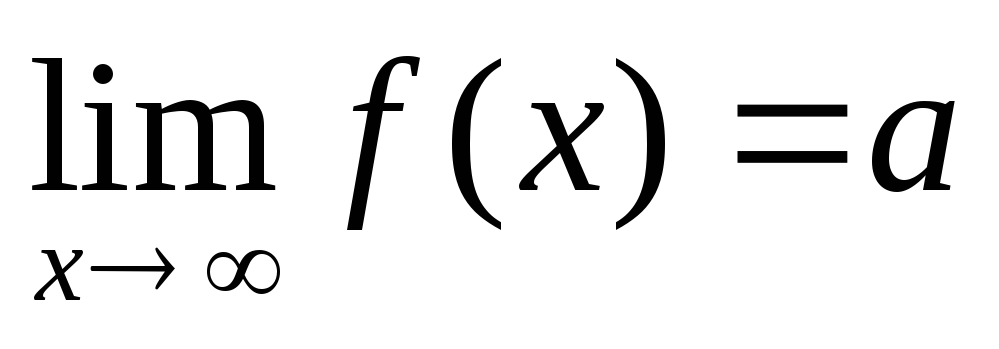7. Какие функции будут удовлетворять определению «предела» функции в точке х₀, если отказаться от условиях_nх₀?

8. Сформулировать отрицание предела функции в точке по Коши и по Гейне.

9. Можно ли в определении 5 заменить на₁, где: а) 0 <₁<, б) ₁>?

10. Существуют ли f(3 +) иf(3 -), если? Существуют ли?

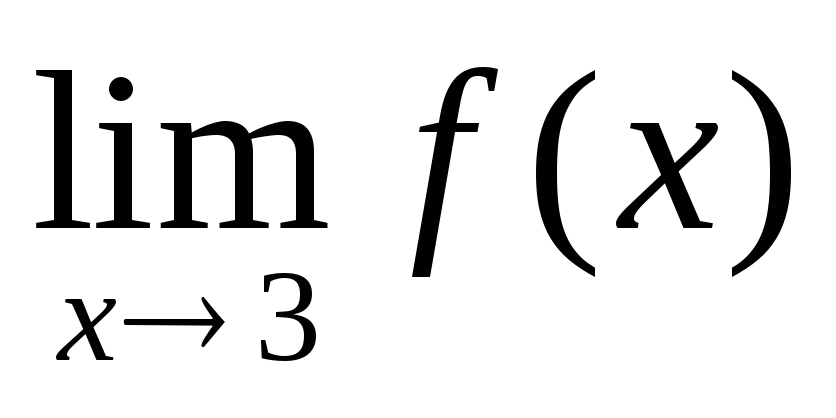11. Сформулировать определение по Коши: . Доказать, что.

12. Доказать по Коши, что .

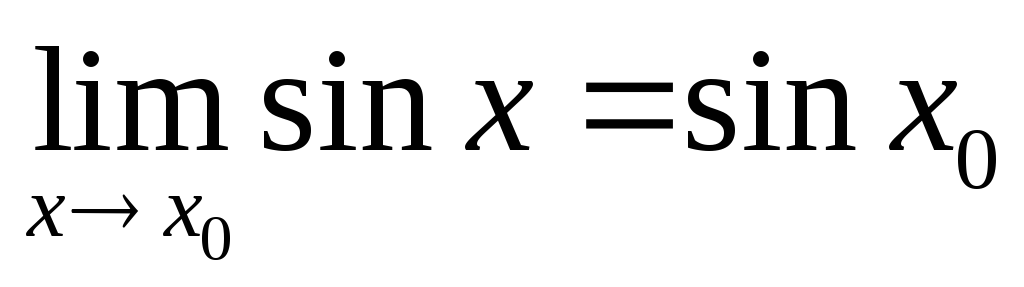13. Доказать, что функция Дирихле не имеет предела ни в одной точке.

14. Если в определении 5 вместо слов «> 0» написать «> 0», то какие функции будут удовлетворять такому определению?