
§ 5. Замечательные пределы и некоторые их свойства.
Т

![]()
Доказательство.Рассмотрим круг
радиусаRс центром в точкеО.
Пусть![]()
![]() ВОА, 0 <х <
ВОА, 0 <х <![]() иСА
иСА![]() ОА
(см. рис.). Тогда
ОА
(см. рис.). Тогда![]() ,
,![]() ,
,![]() .
Из геометрических соображений получим
.
Из геометрических соображений получим![]() <
<![]() <
<![]() ,
откуда в результате преобразований
имеем неравенства 0 < 1 -
,
откуда в результате преобразований
имеем неравенства 0 < 1 -![]() < 1 -
< 1 -![]() .
.
В силу четности здесь всех функций эти
неравенства можно считать верными
![]() .
.
Из левого неравенства следует, что
![]() <
<![]() ,
и потому
,
и потому![]() <
<![]() .
Таким образом,
.
Таким образом,
0 < 1-
![]() <
<![]()
![]() .
.
А так как
![]() ,
то из теоремы о зажатой функции получим
,
то из теоремы о зажатой функции получим![]()
Вставка 1.
Следствие.1)![]() ,
2)
,
2)![]() ,
3)
,
3)![]() ,
4)
,
4)![]() ,
,
5)
![]() ,
6)
,
6)![]() ,
7)
,
7)![]() .
.
Доказательство.1)![]() ;
;
2) 0 <
![]()
![]() ;
;
3)
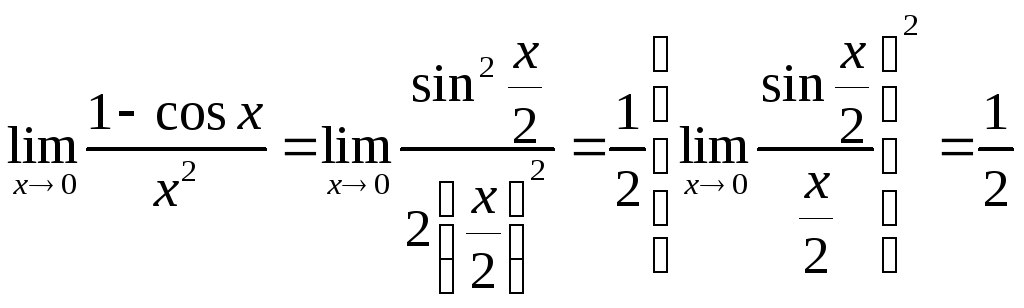 ;
;
4)
![]()
![]()
![]() ;
5)
;
5)![]() ;
;
6)
![]() ;
7)
;
7)![]() .
.
Теорема2 (2-й замечательный
передел).![]() .
.
Доказательство. В§3 гл.IIбыл доказан предел![]() .
.
Пусть х +. Возьмемx > 1. По свойству Архимедаn Nтакое, чтоnх <n + 1. Тогда
![]() .
.
Так как
![]() ,
то по теореме о зажатой функции получим
нужное.
,
то по теореме о зажатой функции получим
нужное.
2) Пусть х. Рассмотримх<1. Тогда

![]() .
.
Теорема доказана.
Следствие. 1)![]() 2)
2)![]()
![]() (в частности,
(в частности,![]()
![]() );
3)
);
3)![]()
![]()
![]() (в частности,
(в частности,![]()
![]() );
);
4)
![]() ;
5)
;
5)![]()
![]() .
.
Действительно:1) .
.
2)Воспользуемся примером![]() ,
тождеством
,
тождеством![]() и теоремой о пределе сложной функции:
и теоремой о пределе сложной функции:
![]()
![]()
![]()

3)![]()
![]()
4)![]()
![]()
![]()
![]() .
.
5)![]()
![]()
![]() .
.
Вопросы и упражнения.
Докажите неравенство 0 < 1 -
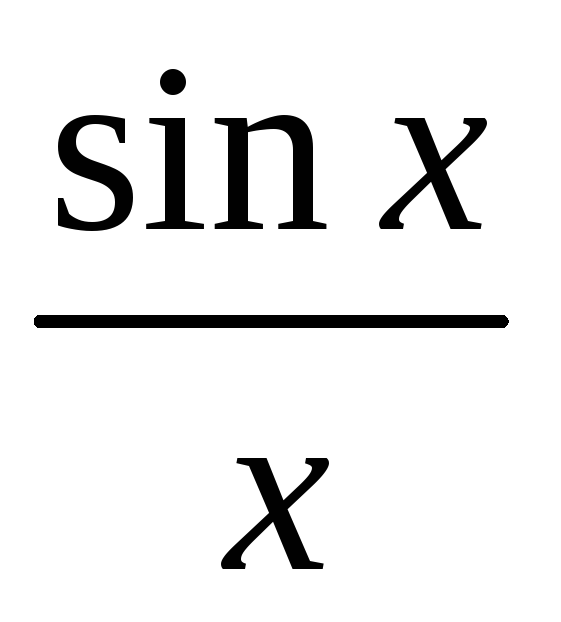 < 1 -
< 1 - при
при (теорема 1).
(теорема 1).Почему при доказательстве теоремы 2 можно было полагать x> 1 илиx< - 1?
Докажите, что
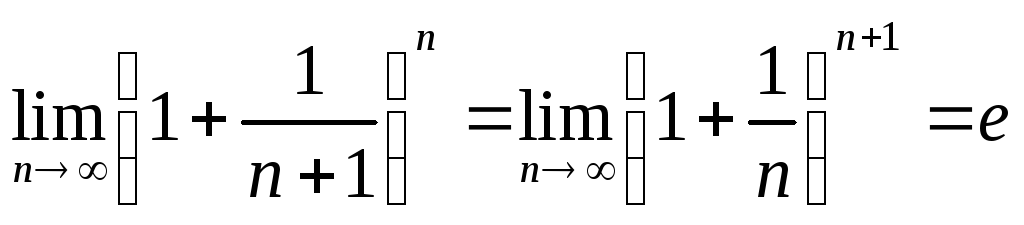 .
.
§ 6. Вычисление пределов.
В следующей главе будет показано, что
если функция
![]() элементарна и точка
элементарна и точка![]() ,
то
,
то![]() В этом случае применимы теоремы о
пределах, поскольку все слагаемые и
сомножители ( значения функций в
предельной точке ) конечны, причем предел
знаменателя (если таковой имеется)
должен быть отличен от нуля.
В этом случае применимы теоремы о
пределах, поскольку все слагаемые и
сомножители ( значения функций в
предельной точке ) конечны, причем предел
знаменателя (если таковой имеется)
должен быть отличен от нуля.
Пример 1.Найти![]() .
.
Решение.Так как функция, стоящая
под знаком предела, элементарна и![]() ,
то
,
то![]()
Таким образом, вычисление пределов от
элементарных функций будет затруднено
только в точках сгущения множества
![]() ,
не принадлежащих
,
не принадлежащих![]() .
Однако здесь иногда оказываются полезными
свойстваб/миб/бфункций.
.
Однако здесь иногда оказываются полезными
свойстваб/миб/бфункций.
Пример 2.Найти![]() .
.
Решение.Так как![]() ,
а
,
а![]() -б/бфункция при
-б/бфункция при![]() ,
то
,
то![]() -б/мфункция при
-б/мфункция при![]() и потому
и потому![]()
Все остальные ситуации представляют неопределенности.
Условимся в обозначениях: ()
-б/бфункция прих
х0; (0) -б/мфункция прих
х0,
отличная от нуля; (1) – функция, не равная
1 и имеющая в точкех0предел,
равный 1. В этих обозначениях виды
неопределенностей можно записать так:![]() (здесьб/бфункции одного знака),
(здесьб/бфункции одного знака),![]() .
Теоретически все неопределенности
можно свести к какой-либо одной из них.
Так, если за исходную взять неопределенность
.
Теоретически все неопределенности
можно свести к какой-либо одной из них.
Так, если за исходную взять неопределенность![]() ,
то:
,
то:
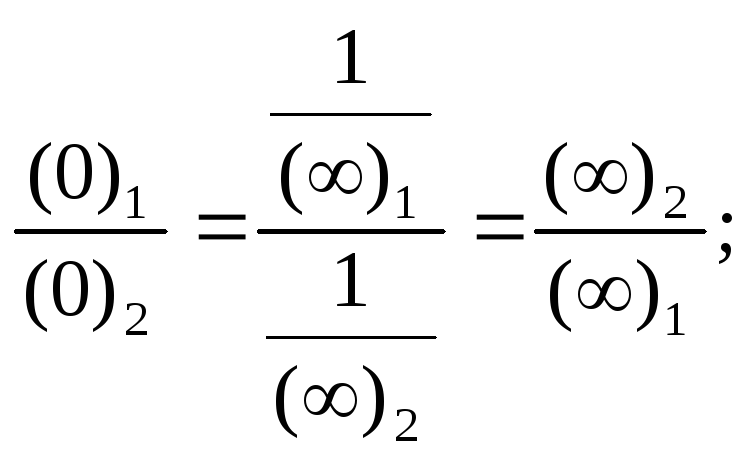
![]() ,
либо
,
либо![]() ;
;
![]()
![]()
неопределенности
![]() логарифмированием сводятся к
неопределенности
логарифмированием сводятся к
неопределенности![]() .
Однако на практике такие преобразования
не всегда удобны. Рассмотрим некоторые
рецепты для раскрытия указанных
неопределенностей.
.
Однако на практике такие преобразования
не всегда удобны. Рассмотрим некоторые
рецепты для раскрытия указанных
неопределенностей.
1.Для раскрытия неопределенности![]() нужно разделить числитель и знаменатель
функции на слагаемое, которое растет
быстрее других (можно без коэффициента)
и воспользоваться теоремами о пределах.
нужно разделить числитель и знаменатель
функции на слагаемое, которое растет
быстрее других (можно без коэффициента)
и воспользоваться теоремами о пределах.
Пример 3.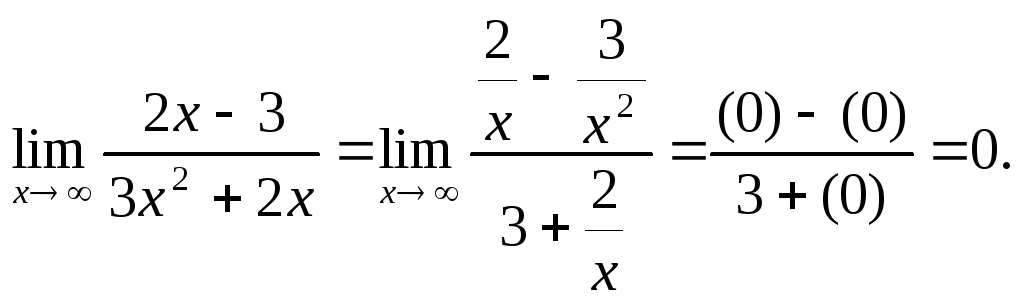
Пример 4.
Ясно, что результат предельного перехода в таких функциях зависит только от высших степеней числителя и знаменателя (см. упр. 1).
2.При раскрытии неопределенности![]() в зависимости от примера можно использовать
следующие приемы.
в зависимости от примера можно использовать
следующие приемы.
2.1.В числителе и знаменателе выделяют
множитель![]() ,
,![]() > 0, после чего производят сокращение.
В случае необходимости операцию
повторяют.
> 0, после чего производят сокращение.
В случае необходимости операцию
повторяют.
Пример 5.![]()
Пример 6.![]()
Можно было сначала сделать замену
![]() ,
тогда
,
тогда
![]()
Если в выражении, стоящем под знаком предела, присутствуют тригонометрические и обратные тригонометрические функции, то полезным оказывается применение первого замечательного предела и его следствий.
Пример 7.![]()
Пример 8.
Пример 9.![]()
Если в выражении, стоящем под знаком предела, участвуют показательная
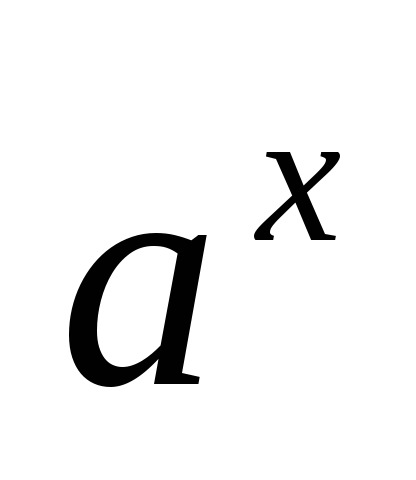 ,
логарифмическая
,
логарифмическая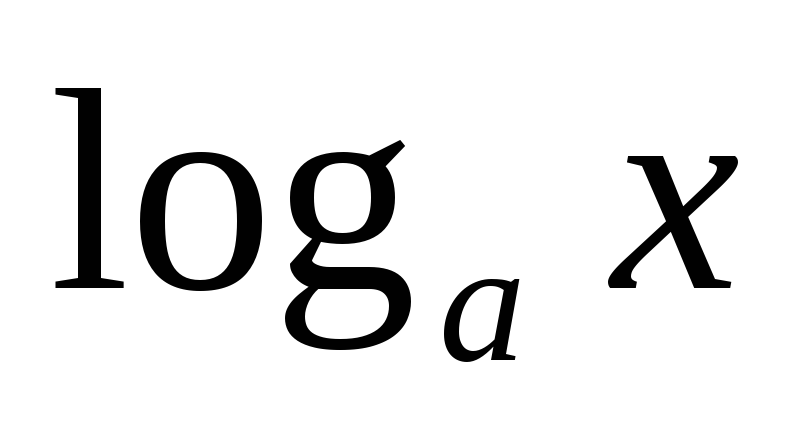 или биномиальная
или биномиальная функции, то полезными оказываются
следствия из второго замечательного
предела.
функции, то полезными оказываются
следствия из второго замечательного
предела.
Пример 10.
Пример 11.![]()
![]()
Пример 12.
При раскрытии неопределенности
 в зависимости от примера выражение,
стоящее под знаком предела, либо приводят
к общему знаменателю, либо избавляются
от иррациональности в числителе.
в зависимости от примера выражение,
стоящее под знаком предела, либо приводят
к общему знаменателю, либо избавляются
от иррациональности в числителе.
Пример 13.![]()
Пример 14.![]()
Неопределенность
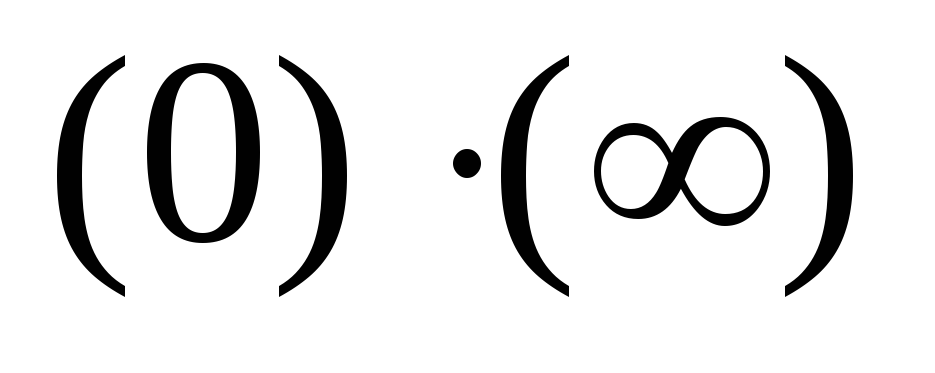 в зависимости от примера сводится к
неопределенностям
в зависимости от примера сводится к
неопределенностям
Пример 15.
![]()
![]()
Неопределенности вида
 путем применения основного логарифмического
тождества сводятся к неопределенности
путем применения основного логарифмического
тождества сводятся к неопределенности .
При раскрытии неопределенности
.
При раскрытии неопределенности можно непосредственно пользоваться
вторым замечательным пределом.
можно непосредственно пользоваться
вторым замечательным пределом.
Пример16.![]()

( здесь и далее
![]() );
либо
);
либо
![]()
![]()
![]()
При вычислении некоторых пределов полезно знание следующих предельных соотношений:
а) б)
б)
в) г)
г)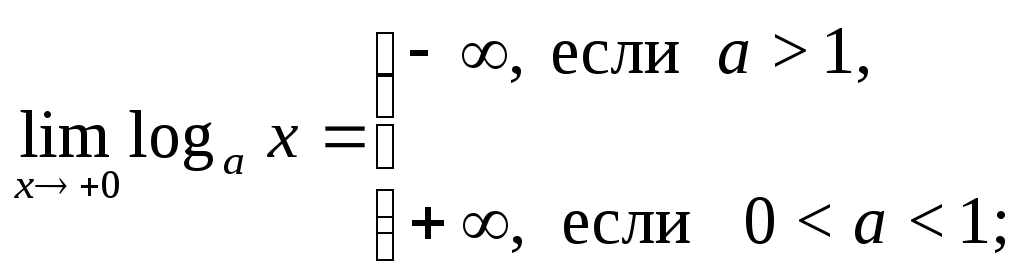
д)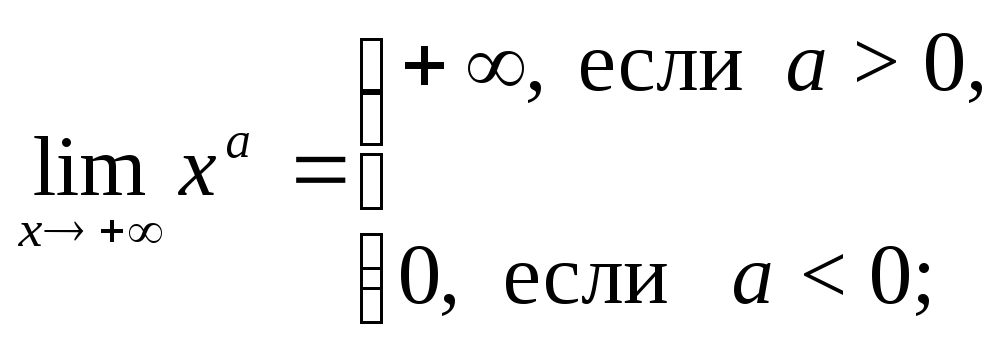 е)
е)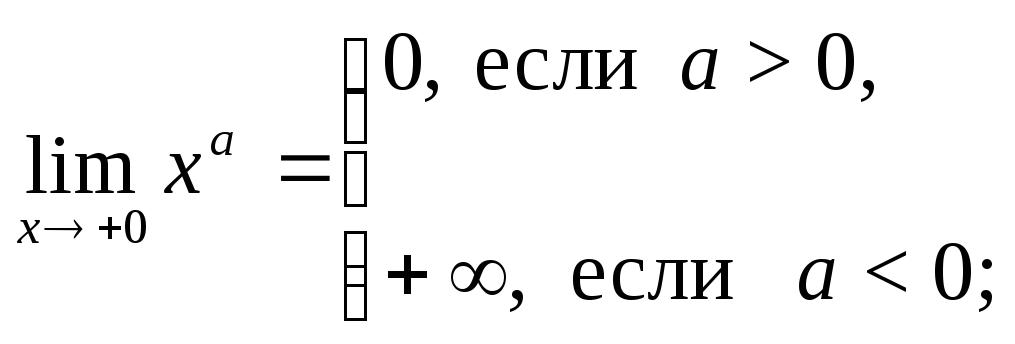
ж)![]()
![]() з)
з)![]()
![]() ;
;
и)![]()
![]() ;к)
;к)![]()
![]()
Пределы а)- е)известны со школы. Рассмотрим пределж).
Пусть
![]() и
и![]() .
Тогда
.
Тогда
![]() .
(4)
.
(4)
Покажем, что
![]()
![]() .
(5)
.
(5)
Можно считать, что
![]() ,
т.к. при
,
т.к. при![]() предел (5) очевиден. Пусть
предел (5) очевиден. Пусть![]() тогда
тогда
![]() , где
, где![]() .
.
Но (бином Ньютона)
 По теореме о «зажатой» функции получим
По теореме о «зажатой» функции получим![]() ,
откуда
,
откуда![]() .
По той же теореме из предыдущего
неравенства получим предел (5).
.
По той же теореме из предыдущего
неравенства получим предел (5).
Далее, из этого предела и неравенства
(4) имеем
![]() ,
или пределж).
,
или пределж).
Если в пределе ж)заменить![]() на
на![]() и возвести в степень
и возвести в степень![]() ,
то получим пределз).Предели)вытекает изз)при замене
,
то получим пределз).Предели)вытекает изз)при замене![]() на
на![]() .
Пределк)при
.
Пределк)при![]() следует изи)с помощью потенцирования.
Если теперь заменить
следует изи)с помощью потенцирования.
Если теперь заменить![]() на
на![]() ,
то получим пределк)при
,
то получим пределк)при![]()
Вопросы и упражнения
1. Пусть![]()
![]() где
где![]() >
0 и
>
0 и![]()
![]() .
Показать, что
.
Показать, что
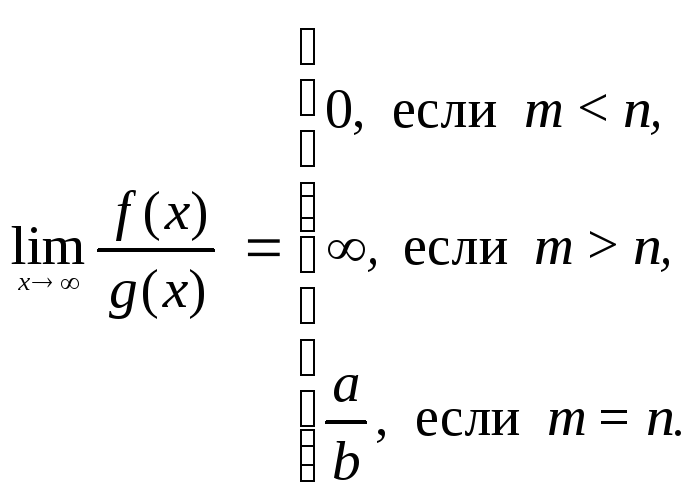
2.Почему в![]() (случай 2.1) можно производить сокращение
на
(случай 2.1) можно производить сокращение
на![]() ,
,![]() >0?
>0?
3.Вычислить пределы:
а)
![]() , б)
, б)![]() , в)
, в)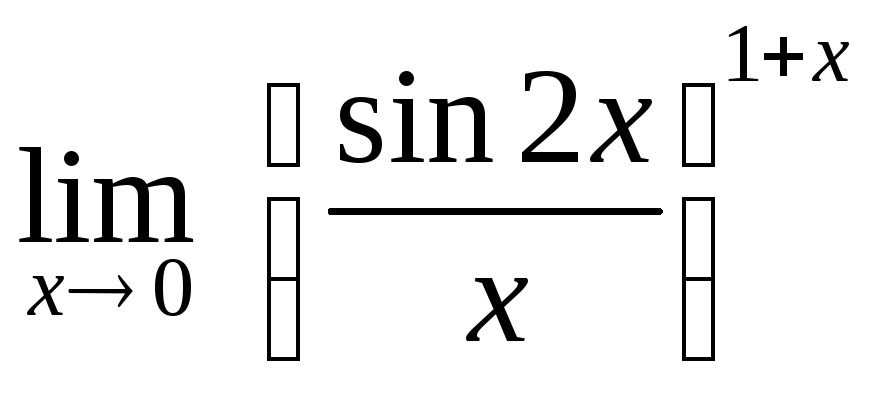 ,
,
г)
 ,
д)
,
д)![]() ,
е)
,
е)![]() ,
,
ж)
![]() ,
з)
,
з)![]() ,
и)
,
и)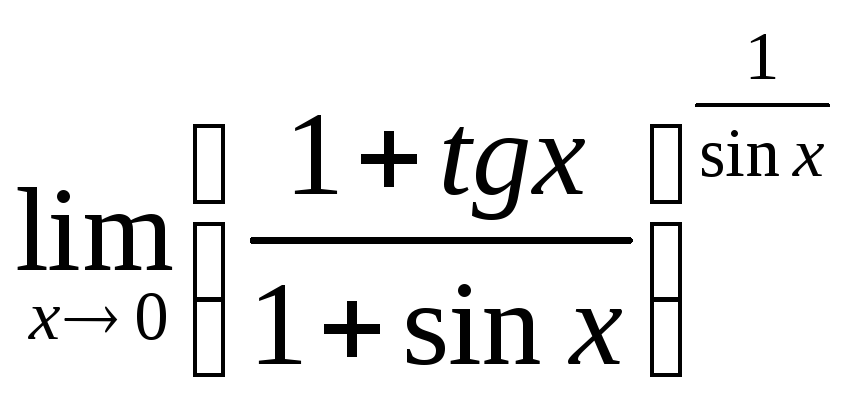 ,
,
к)
![]() ,
л)
,
л)![]() (а> 0), м)
(а> 0), м)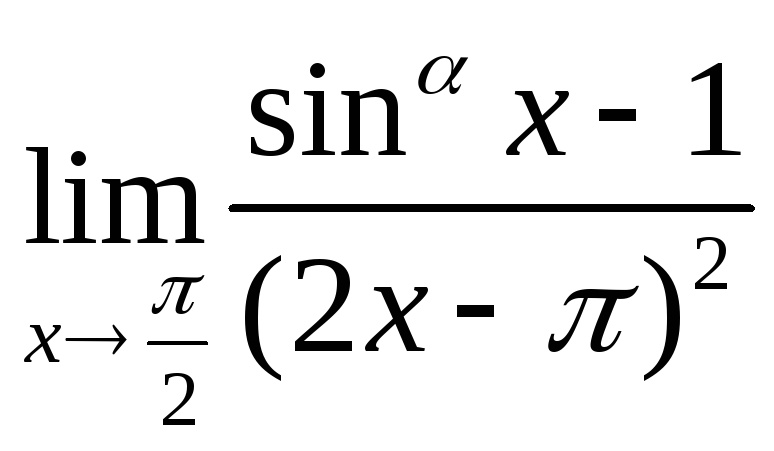 .
.
