4.3. Свойство Архимеда.

Свойство Архимеда для вещественных чисел состоит в следующем.

Теорема.аRnZ:n> an– 1, т.е. множествоZ– неограниченно сверху и снизу.

Доказательство. Докажем левое неравенство. Предположим, что множествоZограниченно сверху. Тогда по теореме (п. 5.2) существуетsupZ=. По свойству 2) утверждения 1n₀Z:n₀>- 1. Но тогдаn₀+ 1 >, причем (n₀+ 1)Z. Это противоречит предположению. Следовательно, свойство Архимеда верно.

Следствие.а, b R (a> 0)nZ:na>b(n– 1)a.

Действительно, достаточно взять, что возможно по доказанной теореме.

С геометрической точки зрения утверждение следствия означает, что каковы бы ни были отрезки длин аиb, a <b, первый отрезок укладывается во втором конечное число раз.

Если в теореме всюду операцию сложения заменить умножением, то получим другой вариант свойства Архимеда.

Теорема1. Если a > 1 и y > 0, то  n  Z: a^{n – 1}  y < aⁿ.

Вставка.

Вопросы и упражнения.

1. Покажите, что в любом ограниченном сверху подмножестве множества Nнайдется наибольший элемент.

2. Покажите, что > 0nN: 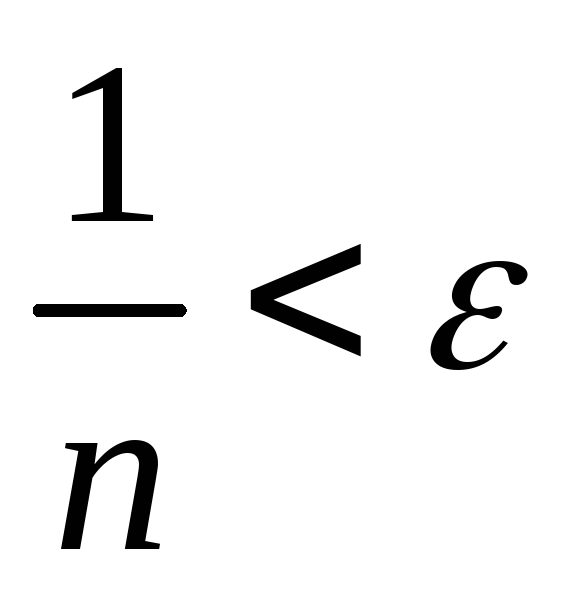. Сделайте отсюда вывод, что.

3. Докажите теорему 1.

§ 5. Расширенная система вещественных чисел. Некоторые числовые множества.

Приведем еще одну геометрическую иллюстрацию вещественных чисел. Рассмотрим числовую прямую и окружность, касающуюся ее в точке О – начале отсчета.

P

-  +

x^’

x0

Пусть ОР - диаметр. Построим отрезок Р, где точкалежит на числовой прямой. Пусть- точка пересечения отрезкаРи окружности. Если исключить из рассмотрения точкуР, то между множеством точек и множеством точекх устанавливается взаимно однозначное соответствие, т.е. каждой точке одного множества отвечает единственная точка другого множества, причем так, что различным точкам отвечают также различные точки. Дополним вещественную ось, а значит, и множество вещественных чисел , двумя символами –и +, которые будут соответствовать точкеР на окружности при рассмотренном правиле взаимно однозначного соответствия.

Определение 1. Под расширенной системой вещественных чисел будем понимать множество =, для элементов которого выполняются следующие условия:

1) R: –<< +,,,;

2) если > 0, то

3) если < 0, то

Если необходимо подчеркнуть различие между символами с одной стороны, и вещественными числами, с другой, то последние будем называтьконечными. Если нас не интересует знак, то будем писать символ

Заметим, что, например, операции илине определены (см. гл.II).

Определение 2. Пусть А  . ЕслиА не ограничено сверху, то будем полагать sup A = + ; если А неограниченно снизу, то inf A = - .

В дальнейшем мы будем оперировать следующими числовыми множествами:

1) сегмент, или отрезок

2) интервал <<

3)окрестность точки

4) проколотая окрестность точки:

5) окрестность точки :где> 0,>0;

6. полусегменты, или полуинтервалы : =(] = [] \ {};

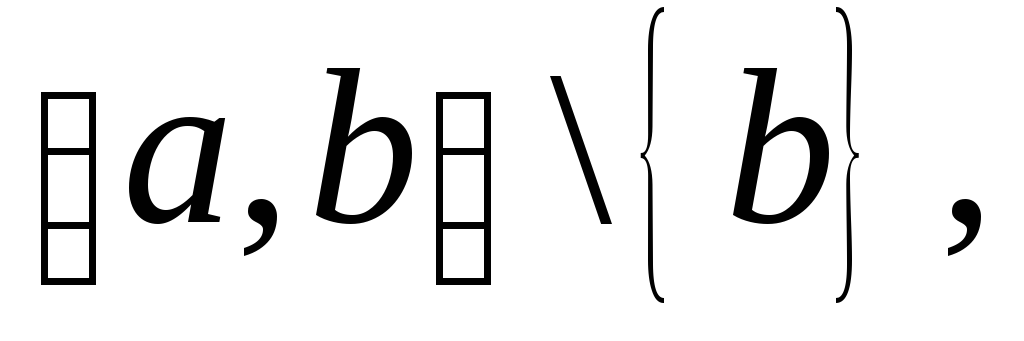7. числовая прямая :

8. полупрямые : [

9. открытые полупрямые: ><

Все указанные множества, кроме 3) и 4), будем называть еще промежутками.

Вопросы и упражнения.

1. Найти sup N, inf Z, sup Q.

2. Определить +  + (+), 2^+, 2^{- }.

3. Записать О_ (а) и с помощью неравенств.

4. Отличаются ли множества и?

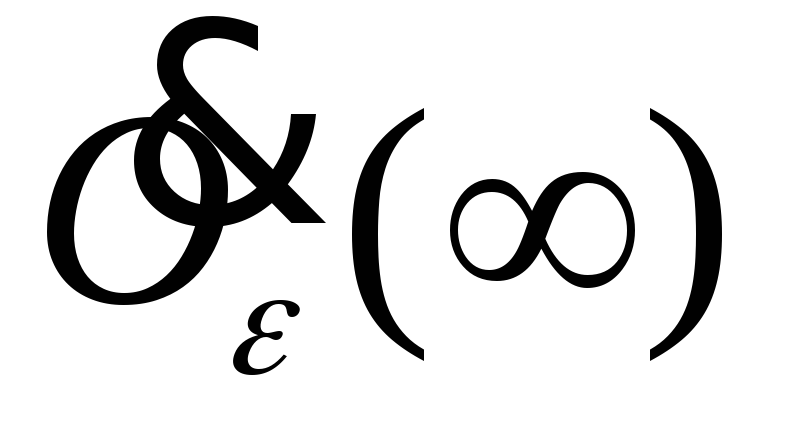5. Будут ли являться окрестностями точки а объединение и пересечение двух и более окрестностей этой точки?

6. Пусть свойство А будет верно в О¹(х₀), а свойство В – в О²(х₀). Укажите точки, для которых верны свойства А и В.