
- •4.1. Функция двух переменных
- •4.2. Основные понятия и определения
- •4.3. Предел функции нескольких переменных
- •4.4. Частные производные и дифференциалы функции нескольких переменных
- •4.5. Связь между дифференцируемостью и существованием частных производных
- •4.6. Связь между дифференцируемостью и непрерывностью функции нескольких переменных
- •4.7.1. Геометрический смысл частных производных
- •4.7.2. Геометрический смысл полного дифференциала
- •4.8. Дифференцирование сложных функций
- •4.9. Инвариантность формы дифференциала
- •4.10. Частные производные и дифференциалы высших порядков
- •4.11. Дифференцирование функций, заданных неявно
- •4.12. Экстремум функции нескольких переменных
- •4.13. Наибольшее и наименьшее значения функции

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
производной (4.4) получаем: |
f (M |
|
) |
|
|
|
o |
|
x |
|
|
A . |
Аналогично доказывается, что |
||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
|
0 |
|
lim A |
|
|
1 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
x1 |
|
|
x |
|
0 1 |
x1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f (M 0 ) |
A . |
Следовательно, частные производные функции в точке |
|
существуют. |
|||||||||||||||||||||||||
x2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя |
Ai |
f (M 0 ) |
для |
|
|
|
в (4.7), получим формулу (4.8) |
|
|
|
|
|
|||||||||||||||||
xi |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение. Частным дифференциалом функции |
|
|
по переменной xk называет- |
||||||||||||||||||||||||||
ся произведение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример. z x2 y ln 3y . Найти полный и частные дифференциалы функции. |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z 2xy dx , d |
|
|
|
1 |
|
► dz |
2xy dx x2 |
|
|
dy - полный дифференциал. |
d |
x |
y |
z |
x2 |
|
dy |
||||||||||||||||||
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
||
- частные дифференциалы по переменным x и y ◄ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Теорема 2 (о достаточном условии дифференцируемости ф.н.п.). Пусть функция |
|||||||||||||||||||||||||||||
определена на множестве |
|
|
|
и имеет в некоторой окрестности точки M 0 X част- |
|||||||||||||||||||||||||
ные производные по всем переменным, |
непрерывные в точке M 0 . Тогда функция |
диф- |
|||||||||||||||||||||||||||
ференцируема в этой точке. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4.6.Связь между дифференцируемостью и непрерывностью функции нескольких переменных
Теорема. Пусть функция определена на множестве |
. Если дифференци- |
руема в точке M0 X , то она непрерывна в этой точке. |
|
Доказательство. Пусть функция дифференцируема в точке M 0 . Тогда по опреде- |
|
лению дифференцируемой функции ее приращение в этой точке представимо в виде |
||||||||
при |
. Отсюда |
lim f (M |
0 ) lim |
A x o |
|
x |
|
0 |
|
|
|||||||
|
|
x 0 |
x 0 |
|
|
|
|
|
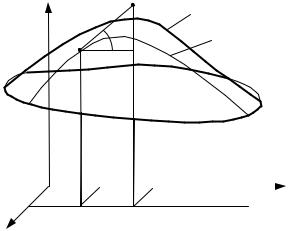
Замечание. Обратное утверждение, вообще говоря, неверно. Из непрерывности функции не следует ее дифференцируемость.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
26 |
|||
4.7. |
Геометрический смысл частных производных и полного дифференциа- |
||||||||||||||||||||
|
|
|
ла функции двух переменных |
|
|
|
|
|
|
|
|
|
|
|
|||||||
4.7.1. |
|
Геометрический смысл частных производных |
|
|
|
|
|||||||||||||||
Рассмотрим функцию двух |
переменных |
и . Пусть |
|
имеет частные производные |
|||||||||||||||||
в точке |
|
. |
Уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
||||||||
|
|
задает |
поверхность |
|
(рис. |
|
|
|
z |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
( ) : z f (x, y) |
||||||||||||
4.5). Зафиксируем переменную |
– |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
пусть |
|
. |
В результате |
получим |
|
|
|
P |
|
|
|
R |
(l) : z f (x0 , y) |
||||||||
|
|
|
|
|
|
||||||||||||||||
функцию |
|
одной переменной . |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Обозначим |
ее |
: |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Графиком этой функции будет кривая |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
, получающаяся |
при |
пересечении |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
поверхности |
|
и плоскости |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Обозначим |
|
|
, |
где |
|
|
|
|
|
|
|
|
x x0 |
|
|||||||
|
|
|
. |
Проведем в точке |
ка- |
|
|
O |
|
y |
|
|
y0 y |
|
|
|
y |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
сательную |
|
к кривой |
. Посколь- |
|
|
|
0 |
|
|
|
|
|
|
|
|||||||
|
|
x0 |
|
|
|
|
|
|
|
|
|
|
|||||||||
ку |
|
|
|
, то из геометриче- |
x |
|
M 0 |
|
|
M |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ского |
смысла |
производной |
функции |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
одной |
переменной |
следует, |
что |
|
|
|
|
|
|
Рис. 4.5 |
|
|
|
|
|||||||
|
|
|
|
|
|
, где |
|
- угол ме- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
жду прямой |
|
, параллельной оси Oy , и касательной |
|
|
к кривой |
в точке . |
|||||||||||||||
Аналогично получаем геометрический смысл частной производной |
|
. |
|
|
|||||||||||||||||
|
|||||||||||||||||||||
4.7.2.Геометрический смысл полного дифференциала
Предположим, что функция |
дифференцируема в точке |
. Тогда ее прира- |
|||
щение в этой точке представимо в виде (4.5): |
|
|
|
||
|
|
|
при |
|
. |
|
|
|
|
||
При доказательстве теоремы 1 из п. 4.5 было получено (с учетом разницы в обозна- |
|||||
чениях), что |
, |
. Тогда |
|
|
|
|
|
|
|
при |
. |
Определение. Плоскость, определяемая уравнением |
|
|
|||
|
|
|
|
, |
(4.9) |
называется касательной плоскостью к поверхности |
в точке |
. |
|||
Поскольку |
|
|
, то из уравнения (4.9) получаем: |
||
Отсюда |
|
|
|
|
|
|
|
|
, |
|
|
где - аппликата касательной плоскости в точке |
, |
. |
|||
Таким образом, |
дифференциал |
равен приращению аппликаты касательной |
|||
плоскости к поверхности |
. |
|
|
|
|
Определение. Нормалью к поверхности |
в точке |
называется |
|||
прямая, перпендикулярная касательной плоскости в точке касания. |
|
||||
