21

4.

Функции нескольких переменных

4.1.

Функция двух переменных

СР

z

Определение. Пусть заданы два множества

z f (M )

,

(множество

задано на плоскости

). Если каждой паре чисел

по неко-

торому правилу

ставится в соответствие число

, то говорят, что на множестве

задана (опре-

делена) функция двух переменных со значениями

во множестве

и пишут

1) или

или

. Также говорят, что задано

O

y

отображение

из множества

во множество .

и

называются независимыми переменны-

(D)

ми, а

– зависимой переменной или функцией.

x

Множество

называют

областью

определения

M (x; y)

функции, а множество

–

множеством значе-

Рис. 4.1

ний функции.

Аналогично определяется функция трех, четырех и более переменных. Функция

переменных задается на

-мерном вещественном пространстве

. Применяются сле-

дующие обозначения: для функции трех переменных -

или

,

для

функции

переменных -

. Во всех случаях применяют обозначение

.

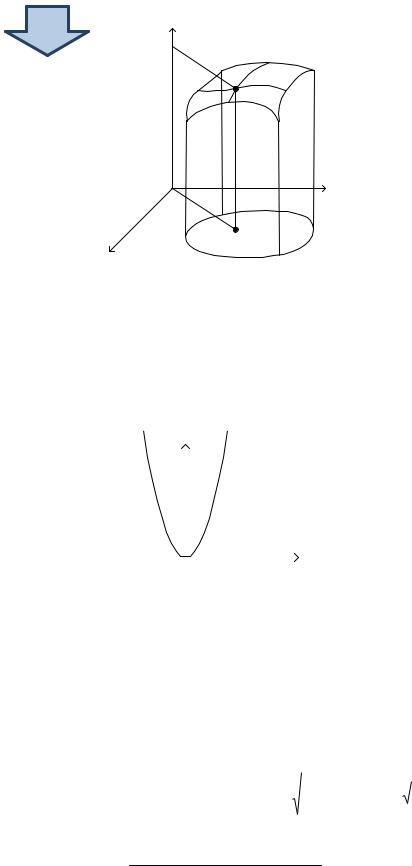
Графиком функции двух переменных является некоторая поверхность (рис. 4.1).

Функции более двух переменных не имеют геометрического представления.

Пример. Найти область определения функции

.

y

►Учитывая область определения логарифма, полу-

чаем:

. Следовательно,

. Границей области определения является парабола

. Граница не принадлежит

, так как неравен-

ство строгое. Берем любую точку, находящуюся не на

x

параболе, например, выше параболы:

. Проверяем,

принадлежит ли эта точка

.

– ложно. Следо-

O

вательно, заштриховываем область ниже параболы (рис.

4.2)◄

Рис. 4.2

Пример.

.

►

. Графиком функции является поверхность

- эллиптический

параболоид. Множеством значений является

◄

Как известно, расстояние в -мерном вещественном пространстве

между двумя

точками

и

находится по формуле:

n

(M1 , M 2 )

( yi

xi )2

( y1 x1 )2 ... ( yn xn )2

(4.1)

i 1

1)

читается так: «функция

задана на множестве и имеет значения во множестве » (или «

отображает множество в множество

», или кратко: «отображение из в »)

22

Определение.

-окрестностью

точки

называется

множество

точек

таких, что расстояние от этих точек до точки M 0 меньше :

U

(M

0

) M Rn : (M

0

, M ) .

Определение. Проколотой

-окрестностью точки

называется множество

точек

, отличных от точки

и таких, что расстояние от этих точек до точки

)

M Rn :

0 < (M

, M ) . Или

) U

меньше : U (M

0

0

U (M

0

(M

0

) \ {M

}.

0

Пространство

можно дополнить бесконечно удаленной точкой .

Определение.

-окрестностью называется множество

U

( ) {M Rn : (M ,O) },

где O(0,..., 0) - начало координат.

Примеры

1.

Пусть

– точка на плоскости

. Тогда

y

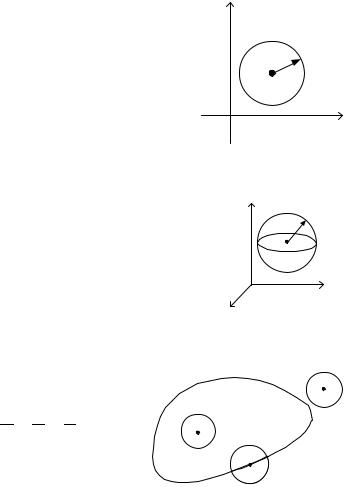
-окрестностью точки M 0

является круг с центром в точке M 0 и

радиусом

без

границы:

(рис.

4 . 2 ),

-окрестностью будет множество

.

M 0

2.

В пространстве

-окрестностью точки

будет шар

x

с центром в

точке

и радиусом

без границы (без сферы):

O

(рис.

4 . 3 ).

-

окрестностью

в

будет множество

Рис. 4.2

. ◄

z

Если множество

содержит свою границу, то множество на-

зывается замкнутым. Если множество

не содержит свою границу,

M 0

то оно называется открытым. Точки множества

,

не принадле-

жащие его

границе, называются внутренними точками множества

O

y

.

x

На рис. 4 . 4

изображено множество . Точка

M

1

- внутренняя

точка множества .

Точка M 2

являются граничной точкой множе-

Рис. 4.3

ства . Точка M 3

не принадлежит множеству .

Пример

M 3

Множество

яв-

M1

ляется замкнутым, так как оно содержит свою границу – эл-

0 ( ) 0 : M U (M0 ) f (M ) U ( A)

(4.3)

Определение.

Пусть x (x , x

2

,..., x

n

) ,

x

0

(x0 , x0

,..., x0 ) . Приращением аргумен-

1

1

2

n

та в точке x0 называется разность

.

Полным приращением функции

в точке x0

называется разность

.

Если приращение придается только k - ой переменной,

то x (0, 0,..., 0, xk , 0,..., 0) . Раз-

ность

f (x

0

) f (x0

,..., x

0

, x0 x

k

, x0

,..., x0 ) f (x0 ,..., x

0 )

xk

1

k 1

k

k 1

n

1

n

называется частным приращением функции в точке x0

по k - ой переменной.

Примеры

1)

Пусть

,

,

. Тогда приращение аргумента в точке

равно

. Найдем соответствующее приращение функ-

ции в точке

.

.

,

.

Следовательно,

2)

Пусть

,

,

,

. Тогда

и со-

ответствующее

приращение

функции

равно

. Теперь придадим приращение только пе-

ременной

:

,

.

Тогда

и

◄

ный предел

x

f (M

0 )

lim

f (x0

,..., x0

, x0

x

, x0

,..., x0 ) f (x0

,..., x0 )

lim

k

1

k 1

k

k

k 1

n

1

n

,

(4.4)

xk

xk

xk 0

xk 0