Киселева Г.А. Математика часть 3

Теорема 1 (о решениях ЛОДУ второго порядка с постоянными коэффициентами):

1.Если k – вещественный корень уравнения (2), то = kr будет решением уравнения (1).

2.Если числа α + tβ и α − tβ – комплексные корни уравнения (2), то = kv cos β и = kv sin β - решения уравнения (1).

Замечание: если k - вещественный корень уравнения (2), при этом дискриминант равен 0, то = ∙ kr будет решением уравнения (1).

Теорема 2 (об общем решении ЛОДУ второго порядка с посто-

янными коэффициентами).

1. Если корни уравнения (2) действительные различные (D > 0,

k1 ≠ k2), то общее решение уравнения (1) имеет вид: nn = ABkrL + + A krM .

3) y′′ − 2 y′ + 2 y = 0

31

k 2 − 2k + 2 = 0 − характеристическое уравнение.

D = −4 = 4i2

k1 = 1 − i, k2 = 1+ i,

yoo = ex (C1 cos x + C2 sin x).

5.ЛНДУ второго порядка с постоянными коэффициентами

справой частью специального вида

ЛНДУ второго порядка с постоянными коэффициентом имеет вид ′′ + [ ′ + e = , где p, q – некоторые числа, f(x) – непрерывная функция.

Известно, что он = оо + чн.

Если в правой части ЛНДУ второго порядка с постоянными коэффициентами стоит многочлен, или показательная функция kv , или тригонометрическая функция sin β , cos β , или линейная комбинация перечисленных функций, то есть правая часть имеет так называемый специальный вид, то частное решение может быть найдено методом неопределенных коэффициентов, не содержащим процесса интегрирования.

Пусть правая часть исходного уравнения имеет специальный вид = kz •3 cos y + •€ sin y , где α, β – некоторые дей-

ствительные числа, •3 – многочлен степени n от x, •€ – многочлен степени m от x.

Тогда частное решения данного неоднородного уравнения может быть найдено по формуле

чн = kv (•B( ) cos β + • ( ) sin β ) ‚,

где α, β – числа из правой части f(x), •B( ), • ( ) – многочлены с неопределенными коэффициентами степени max{…, ~}, s – число корней характеристического уравнения соответствующего однородного уравнения q + [q + e = 0, равных α + βt, (s может быть = 0, 1, 2).

Замечание: многочлены с неопределенными коэффициентами имеют вид: нулевой степени – А; первой степени – ( Ax + B); второй степени – ( Ax2 + Bx + C) и так далее.

32

Пример.

y′′ − 2 y′ + y = x + 1,

y′′ − 2 y′ + y = 0 − соответствующее однородное уравнение.

k 2 − 2k + 1 = 0 − характеристическое уравнение.

D = 0, k1 = k2 = k = 1. yoo = C1ex + C2 xex .

нение

−2A + Ax + B = x +1

А= 1} yчн = x + 3

В= 3 y oн = C1ex + C2 xex + x + 3.

Теорема. Пусть дано ЛНДУ второго порядка с постоянными коэффициентами ′′ + [ ′ + e = B( ) + ( ) ( ), правая часть которого есть сумма двух функций специального вида. Если чнB – частное решение уравнения ′′ + [ ′ + e = B( ), а чн – частное решение уравнения ′′ + [ ′ + e = ( ), то частное решение исходного уравнения (*) будет равно чн = чнB + чн .

Пример.

y′′ − y′ = x2 +1− ex

y′′ − y′ = 0 − соответствующее однородное уравнение.

k 2 − k = 0 − характеристическое уравнение. k1 = 0, k2 = 1.

yoo = C1 + C2ex

f(x) = x2 + 1 − ex

f1 ( x) f2 ( x)

f1 (x) = x2 +1

33

α = 0, β = 0, n = 2, s = 1

Dex (x + 2) - Dex (x +1) = -ex Dex (x + 2 - x -1) = -ex

Dex = -ex

D = -1. y2 = − xex

yон = yoo + yчн , yчн = y1 + y2 ,

тогда yон = C1 + C2ex - 1 x3 - x2 - 3x - xex . 3

34

6. Дифференциальные уравнения высших порядков, допускающие понижение порядка

ДУ n – порядка имеет вид: 45 , , ′, … , 3 6 = 0.

Если его можно разрешить относительно старшей n-й производной, то уравнение примет вид:

3 = 5 , , ′, … , 3TB 6. (*)

Далее будем рассматривать ДУ высших порядков типа (*).

Теорема (о существовании и единственности решения). Если в ДУ (*) функция f и ее частные производные по аргументам y, y’, …, y(n - 1) непрерывны в некоторой области, содержащей точку x = x0, y = y0, y’ = y’ 0, …, y (n - 1) = y0(n - 1), то существует и при том единственное решение уравнения (*), удовлетворяющее условиям

( ) = , ( ) = , … , (3TB)( ) = (3TB)

′ ′ .

Рассмотрим уравнения высших порядков, допускающие понижения порядка.

1. Уравнение вида: (3) = ( ) (в уравнении нет y, y’, …, y(n - 1))

Интегрируя по х левую и правую части получим

(3TB) = J ( )H + AB.

Снова интегрируем

(3T ) = J(J ( )H ) H + AB + A .

И так далее

После n-интегрирований получим общее решение.

35

Пример.

Для нахождения частного решения подставим начальные усло-

держит явно y и может не содержать производных до порядка (k – 1) включительно)

решая его k-кратным интегрированием получим общее решение исходного уравнения.

36

Пример.

Найти общее решение уравнения y′′ − 3y′ = x. x

Вводим новую функцию: z(x) = y′, z′(x) = y′′.

далее.

Таким образом, порядок уравнения понижается на 1.

37

Пример.

Найти общее решение уравнения 1+ ( y′)2 = y × y′′

y′ = p( y),

Делаем подстановку: y¢¢ = p dp . dy

1 + p2 = y × p dp – это уравнение с разделяющимися переменны- dy

ми.

ln y2 + ln C12 = ln(1 + p2 )

С12 y2 = 1 + p2

p = ±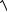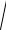С12 y2 -1.

Тогда

y¢ = ± 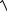С12 y2 -1

dy

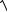
∫ С12 y2 -1 = ±∫ dx

38

РЕШЕНИЕ ПРИМЕРНОГО ВАРИАНТА КОНТРОЛЬНОЙ РАБОТЫ

Задача 1

Правая часть является однородной функцией нулевой степени, так как

Следовательно, исходное уравнение является однородным.

Делаем замену z = y , y′ = z + xz′ . x

z + xz′ = 4z2 + z + 4 xz′ = 4(z2 +1)

39

arctg z = 4 ln x + ln C arctg z = ln Cx4

Подставим z = y , тогда arctg y = ln Cx4 - общий интеграл. x x

Ответ: arctg y = ln Cx4 x

Задача 2

Решить уравнение и сделать проверку: y′ − y = xex .

Решение

y′ − y = xex - это линейное дифференциальное уравнение первого порядка.

dv = v dx

dv = dx v

∫ dvv = ∫ dx

ln v = x (считаем постоянную равной 0, так как ищем одну из первообразных)

Тогда v = ex . Подставим v в уравнение (*)

u¢ × ex = xex u′ = x

u = ∫ xdx

40