
Киселева Г.А. Математика часть 2
.pdf
|
|
x4 x3 1 |
= x |
2 |
– 2x + 4 + |
|
|
|
8x 9 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
x2 |
|
x |
2 |
|
|
|
|
x2 x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Рассмотрим |
|
дробь |
|
|
|
8x 9 |
|
. Это |
|
правильная |
рациональная |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
x2 x 2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
дробь. Представим ее в виде суммы простейших: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
8x |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
8x |
|
|
|
9 |
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
B |
|
|
|
|
A |
|
x 2 |
|
B |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
x 1 |
, |
||||||||||||||||||||||
|
|
x2 x 2 |
|
x 1 x 2 |
|
x 1 |
x 2 |
|
|
|
|
|
x 1 x 2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
– 8x + 9 = A (x + 2) + B (x – 1), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x = 1 |
–8 + 9 = 3A A = |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = –1 |
16 + 9 = –3B B = – |
25 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8x 9 |
|
|
|
|
|
= |
1 |
|
|
|
|
1 |
|
|
|
|
|
25 |
|
|
|
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
x2 x |
2 |
|
|
3 |
|
|
x |
1 |
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
Таким образом, исходный интеграл: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
x |
4 x3 |
1 |
dx |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
25 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
x |
|
|
|
2x 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx = |
|
|
|
|
||||||||||||||||||||
|
|
x2 x |
2 |
|
|
|
3 |
|
x |
1 |
3 |
x 2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
= x2dx 2 x dx + 4 dx |
1 |
|
dx |
|
|
|
|
|
25 |
|
|
dx |
|
= |
|
x3 |
x2 4x |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
x 1 |
|
3 |
|
|
x |
2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
1 ln |
|
x 1 |
|
|
|
25 ln |
|
x 2 |
|
C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
31
1.5. Интегрирование некоторых классов функций
1) |
|
R sin x, cos x dx, |
где R (sin x, cos x) – рациональная функ- |
|||||||||||||||||||||||||||||||||||||||||||||||||
ция |
|
|
|
от sin x и cos x, находится |
|
с помощью замены t tg |
x |
. При |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 dt |
|
|
|
|
|
|
|
|
|
2t |
|
|
|
|
|
|
|
|
1 |
t |
2 |
|
|
|
|
||||||||
этом |
|
x = 2 arctg t, dx |
|
|
|
, |
sin x |
|
|
, cos x |
|
. |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
1 |
t2 |
|
|
1 t2 |
1 |
t |
2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Пример |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 t2 |
|
|
|
|
|
|
|
|
|
|
|
2 dt |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
= |
|
|
cos x |
1 t |
2 |
|
|
|
= |
|
|
|
|
|
1 t |
2 |
|
|
|
|
|
|
= |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
5 4sin x |
3cos x |
|
|
1 t |
2 |
|
|
|
5 4 |
|
|
2t |
|
|
|
3 |
1 t |
2 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 dt |
|
|
|
|
|
|
|
|
1 |
t2 |
|
|
1 t2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= |
|
|
|
|
|
|
|
2 dt |
|
|
|
|
= |
|
|
|
|
|
|
dt |
|
|
|
|
= |
|
dt |
|
= |
t 2 1 C = |
||||||||||||||||||||||
5 |
|
|
5t |
2 |
8t |
3 3t |
2 |
|
t |
2 |
4t 4 |
|
t 2 |
2 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||||||||||||
= |
|
|
|
1 |
|
|
C = |
1 |
|
|
|
|
|
C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
t |
|
2 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
tg |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Замечание. |
Подстановка |
|
|
t tg |
x |
|
называется |
|
универсальной |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тригонометрической подстановкой. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
б) |
|
R sin x cos x dx находится |
с помощью замены t = sin x, |
|||||||||||||||||||||||||||||||||||||||||||||||||
при этом cos x dx = dt. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
R cos x sin x dx |
|
|
находится |
|
с помощью замены t = соs x, |
||||||||||||||||||||||||||||||||||||||||||||||
при этом sin x dx = –dt.
sinn x cosm x dx находится с помощью замены:
32
– если n |
нечетное, |
то |
t |
= |
соs x, |
при этом |
sin 2x = 1 – t 2, |
|||
sin x dx = –dt; |
|
|
|
|
|
|
|
|
|
cos 2x = 1 – t 2, |
– если m |
нечетное, |
то |
t |
= |
sin x, |
при этом |
||||
cos x dx = dt. |
|
|
|
|
|
|
|
|
|
|
Пример |
|
|
|
|
|
|
|
|
|
|
sin3 x cos2 |
|
t cos x |
|
|
= 1 t2 t2 dt = t4dt |
|||||
|
|
|
||||||||
x dx = |
sin2 x 1 t2 |
|||||||||
|
|
|
sin x dx dt |
|
|
|
||||
|
|
|
|
|
|
|
||||
t2dt = t5 t3 |
C = cos5 x |
cos3 x |
C . |
|
|
|||||
5 |
3 |
|
|
5 |
|
|
3 |
|
|
|
в) sin αx |
cosβx dx, |
sin αx sin βx dx , |
cos αx cosβx dx сводятся |
|||||||
к табличным интегралам с помощью тригонометрических формул:
sin αx cosβx 12 sin α β x sin α β x , sin αx sin βx 12 cos α β x cos α β x , cos αx cosβx 12 cos α β x cos α β x .
|
Пример |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 5x cos3x dx = 1 |
sin 8x sin 2x dx = |
1 |
sin 8x dx |
||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
1 sin 2x dx = |
1 |
|
1 |
cos8x |
1 |
|
1 |
cos 2x C = |
|
1 |
cos8x |
||||
2 |
8 |
2 |
2 |
16 |
||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|||||||
|
1 cos 2x C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
33
г) R x, |
|
n ax b dx |
находится с помощью замены t n ax b , |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
tn b |
|
|
|
n |
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
, dx a t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
при этом x |
|
a |
|
dt . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Пример |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
x |
|
|
|
|
|
|
|
x 1 t2 |
|
= t2 1 2t |
dt = 2 t2dt 2 dt = |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
dx |
= |
|
x t2 1 |
|
|
|
||||||||||||||||||||||||||
|
|
x 1 |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
dx 2t dt |
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= 2 t3 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
2t C = |
x 1 3 |
|
2 x 1 C . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
д) |
R x, |
|
|
a2 x2 dx |
находится с помощью замены x = a sin t |
||||||||||||||||||||||||||||||
(или x = a cos t), |
при этом |
|
|
a2 x2 |
a cost |
(или a2 x2 |
a sin t ) |
||||||||||||||||||||||||||||
и dx = a cos t |
(или dx = –a sin t). |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
R |
x, |
a2 x2 dx |
находится |
с помощью замены |
x = a tg t |
||||||||||||||||||||||||||||||
(или x = a ctg t), |
при этом |
|
|
a2 x2 |
|
|
a |
(или a2 x2 |
|
|
a |
) |
|||||||||||||||||||||||
|
|
cos t |
sin t |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
и dx |
|
a |
|
|
dt |
(или dx |
|
|
|
a |
|
dt ). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
cos2 t |
|
sin2 t |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Пример |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
x 1 |
|
|
dx = |
|
|
x 1 |
|
|
|
|
|
|
x 2 2 sin t |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
dx = |
|
|
x 2 sin t 2 |
|
|
= |
|
|
|
|
|||||||||||||||||
|
4 x x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
4 |
x 2 2 |
|
|
|
dx 2 cos t dt |
|
|
|
|
|
|
|
|||||||||||||||
= 2 sin t 3 |
2 cos t dt |
= 2 sin t dt |
+ 3 dt = 2 cos t 3t C |
= |
|
||||||||||||||||||||||||||||||
|
|
2 cos t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
34

= 4x x2 3arcsin x 2 C . 2
2. Определенный интеграл
2.1. Определение и свойства определенного интеграла
Пусть на отрезке [a; b] |
задана непрерывная функция f (x). |
|
Разобьем [a; b] на n |
частей произвольной последовательно- |
|
стью точек a = x0 < x1 < < xn = b. |
|
|
Выберем на каждом элементарном отрезке [x k – 1, x k] |
произ- |
|
|
n |
|
вольную точку ck . Тогда |
f ck xk , где xk xk xk 1 |
– ин- |
k 1
тегральная сумма для функции f (x) на [a, b], соответствующая данному разбиению отрезка и данному выбору промежуточных точек.
Если существует предел интегральной суммы для функции f (x) на [a, b] при стремлении к 0 длины наибольшего элементарного отрезка, не зависящий от способа разбиения отрезка на элементарные части, от выбора промежуточных точек в каждом элементарном отрезке, то этот предел называют определенным интегра-
b
лом от функции f (x) на [a, b] и обозначают f x dx .
a
При этом a – нижний предел интегрирования, b – верхний предел интегрирования.
Теорема. Если функция f (x) непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.
Свойства определенного интеграла
a
1. f x dx 0 .
a
35
|
b |
|
|
|
2. |
dx b a . |
|
|
|
|
a |
|
|
|
|
b |
a |
|
|
3. |
f x dx f |
x dx . |
|
|
|
a |
b |
|
|
|
b |
b |
|
|
4. |
k f |
x dx k f x dx . |
|
|
|
a |
a |
|
|
|
b |
|
b |
b |
5. |
f1 |
x f2 x dx f1 |
x dx |
|
|
a |
|
a |
a |
|
b |
c |
b |
|
6. |
f |
x dx f |
x dx f x dx |
|
|
a |
a |
c |
|
f2 x dx .
для любых чисел a, b, c
(при условии, что все три интеграла существуют).
7. Если функции f (x) и (x) интегрируемы на [a; b] и если для любого x [a; b] выполняется f (x) (x), то
|
|
b |
|
b |
|
|
|
|
|
|
f x dx x dx . |
||||||
|
|
a |
|
a |
|
|
|
|
8. |
Если m и M – |
наименьшее и наибольшее значения функ- |
||||||
|
|
|
|
b |
|
|
|
|
ции |
f (x) на [a; b], то |
m b a f x dx M b a . |
||||||
|
|
|
|
a |
|
|
|
|
|
|
b |
|
b |
|
|
|
|
|
|
|
|
|
|
|
||
9. |
Если a b, то |
f x dx |
|
|
|
f x |
|
dx. |
|
|
|
||||||
|
|
a |
|
a |
|
|
|
|
10. Теорема о среднем. Если функция f (x) непрерывна на [a; b], то на [a; b] существует точка c такая, что
36

b
f x dx b a f c .
a
2.2. Формула Ньютона – Лейбница
Если F(x) – одна из первообразных для функции f (x) на [a; b],
b
то f x dx F x ba F b F a .
a
Примеры
|
b |
|
|
x4 |
|
|
b |
b4 |
a4 . |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1. |
x3dx |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
a |
|
|
4 |
|
a |
4 |
|
4 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
dx |
|
|
|
|
|
1 |
|
|
|
|
π |
|
|
π |
|
π |
|
|||
2. |
1 |
arctg x |
=arctg 1 arctg ( 1) |
|
|
. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1 x2 |
1 |
4 |
4 |
2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1 |
2x dx2 ln 1 x2 |
|
|
10 |
|
|
|
|
|
|
|
|
|
||||||||
3. |
|
|
ln 2 ln1 ln 2. |
|
|
|
|
|
|
|
|
|||||||||||
|
0 |
1 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2.3. Методы интегрирования определенного интеграла
а) Замена переменной |
|
|
|
|
Пусть функция |
f (x) непрерывна на |
[a, b]. |
Если x = φ (t), |
|
φ (α) = a, φ (β) = b, функции φ (t), |
φ (t), f (φ (t)) |
непрерывны на |
||
[α; β], то |
|
|
|
|
b |
β |
t |
t dt . |
|
|
f x dx f |
|
||
|
|
|
|
|
a |
α |
|
|
|
37

Пример
|
|
|
|
1 x2 |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
|
|
|
-2xdx dt |
|
|
3 |
|
|
3 |
|
|
|
|
|
|||||||
2 |
xdx |
|
|
|
|
1 |
|
|
|
1 |
4 |
dt |
|
|
3 |
|
3 |
|
||||
|
|
x |
0 |
|
|
= |
|
t |
|
4 |
= |
1 = 1 |
. |
|||||||||
1 x2 |
|
|
2 |
t |
2 |
2 |
||||||||||||||||
|
|
|
|
|||||||||||||||||||
0 |
|
|
|
|
2 |
|
|
|
1 |
|
|
|
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
t |
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) Интегрирование по частям
Пусть функции u и v дифференцируемы на [a, b] и на этом отрезке u, v, u , v непрерывны. Тогда
|
|
|
b |
|
|
|
b |
||||
|
|
|
u dv u v |
|
ba v du . |
||||||
|
|
|
|
||||||||
|
|
|
|
||||||||
|
|
|
a |
|
|
|
a |
||||
Пример |
|
|
|
|
|
|
|
|
|
|
|
e |
|
u ln x |
du |
dx |
|
|
|
|
e |
||
|
|
|
|
|
|||||||
ln x dx |
|
x |
= x ln x |
|
1e dx = e ln e ln 1 x |
|
1e = |
||||
|
|
|
|||||||||
|
dv dx |
v x |
|
|
|||||||
1 |
|
|
1 |
|
|
||||||
= e e 1 1.
2.4. Геометрические приложения определенного интеграла.
2.4.1. Вычисление площадей плоских фигур
b
Геометрический смысл определенного интеграла: f x dx
a
выражает площадь криволинейной трапеции, ограниченной сверху кривой y = f (x), слева и справа прямыми x = a и x = b и опирающийся на [a, b] оси OX:
38
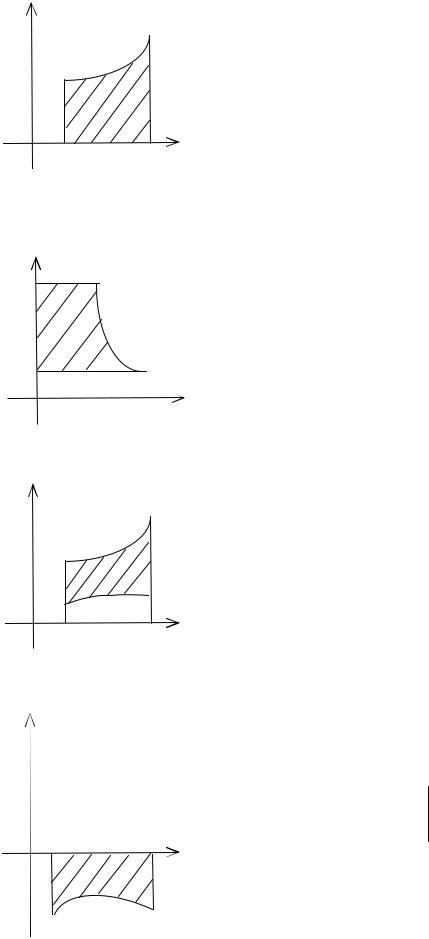
y |
b |
y = f (x) |
S f x dx |
|
a |
0 a b x
Частные случаи: |
|
|
|
|||
а) |
y |
|
|
|
|
|
|
d |
|
|
d |
|
|
|
|
|
x = φ(y) |
S y dy |
|
|
|
|
|
|
c |
|
|
|
c |
|
|
|
|
|
|
0 |
|
|
x |
|
|
б) |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
y = f (x) |
S b |
f x g x dx |
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
y = g (x) |
|
|
|
|
0 |
a |
b |
x |
|
|
в)
y
|
|
b |
|
b |
|
|
|
||
a |
b |
S f x dx |
|
f x dx |
a |
|
a |
||
0 |
|
x |
|
|
y = f (x)
39
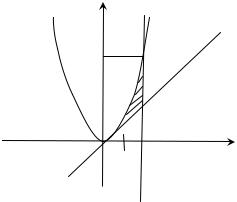
Пример. Вычислить площадь фигуры, ограниченной линия-
ми y = x, y = x 2, x = 2.
Построим заданную фигуру:
y
y = x2 |
4 |
y = x |
0 |
1 2 |
x |
x = 2
2 |
2 |
2 |
|
x |
3 |
|
|
2 |
|
x |
2 |
|
|
2 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
||||||||
S x2 |
x dx = x2dx x dx = |
|
|
|
|
|
|
|
|
|
= |
||||
3 |
|
|
2 |
|
|
||||||||||
1 |
1 |
1 |
|
|
|
1 |
|
|
|
1 |
|
||||
|
|
|
|
|
|
|
|||||||||
|
8 |
|
1 |
|
|
4 |
|
1 |
|
|
5 |
2 |
= |
3 |
3 |
|
|
2 |
2 |
|
6 |
(ед ). |
|||
|
|
|
|
|
|
|
|
Замечания
1. Если кривая, ограничивающая криволинейную трапецию, задана параметрически:
x x t |
|
|
, |
|
|
y y t |
|
|
|
то
где ≤ t ≤ β, |
x ( ) = a, x (β) = b, |
S y t x t dt .
40
